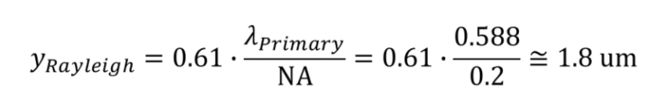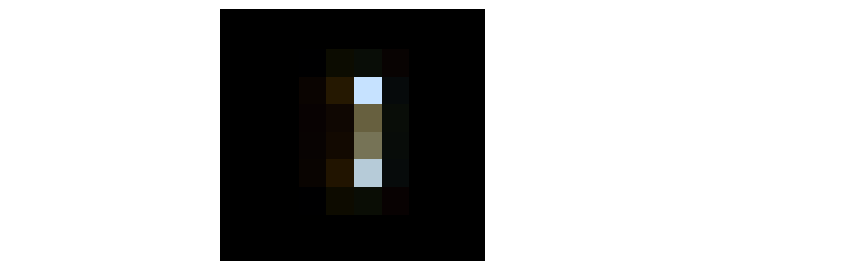ZEMAX | 使用点扩散函数的衍射极限成像系统的分辨率
ZEMAX | 使用点扩散函数的衍射极限成像系统的分辨率
成像系统(例如显微镜)的衍射极限分辨率可以通过不同方式表征。在本文中,我建议使用在 OpticStudio 中计算的点扩散函数 (PSF) 来客观衡量这些成像系统的分辨率。文中介绍了重叠图像(探测器)平面上两个点的 PSF 的两种方法。第一种方法使用多重结构编辑器,第二种方法使用图像模拟工具。文中比较了这两种方法,并讨论了它们的优缺点。(联系我们获取文章附件)
简介
成像系统的性能与其分辨率有关,但分辨率的定义各不相同。在超分辨率显微镜中,傅里叶环相关[1]用于评估分辨率。在衍射极限显微镜中,分辨率是用瑞利或斯派罗准则估算的[2]。在实践中,这些系统的分辨率也可以用微粒测量,微粒选择明显小于预期分辨率,选定上述标准之一。这些微粒充当形成 PSF 的点发源,其尺寸给出了图像分辨率的估计值,同样,该尺寸根据其定义而变化。在本文中,我们使用 OpticStudio 中的 PSF 来更客观地评估衍射极限成像系统的分辨率。
方法一:多重结构编辑器(相干成像)
显微镜设计
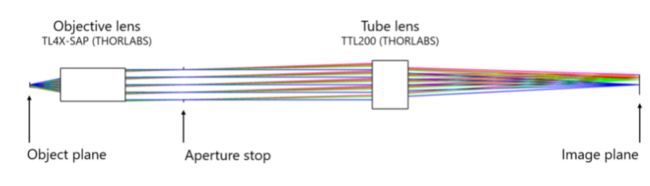
在整篇文章中,我使用了基于 TL4X-SAP 物镜(4X,0.2 NA)和 TTL200 管镜的显微镜设计,如图1所示。这两种透镜都可由 THORLABS 网站以黑盒形式提供。
图 1 - 由 THORLABS 的黑匣子元件组成的显微镜设计。放大倍数为 4X,数值孔径 (NA) 为0.2。
我们使用“真实图像高度”定义并指定了在 X 和 Y 半宽为6.656毫米的正方形上具有相等面积的五个视场,对应于物平面中的1.664毫米。视场由像面中具有2048x2048像素和13.312x13.312mm2物理尺寸的科学 CMOS (sCMOS) 探测器进行建模。这些探测器通常用于显微镜,可以在 Orca-Flash4.0 V3 (Hamamatsu) 或Zyla 4.2 plus (Andor) 等相机产品中找到。我还使用了 OpticStudio 的波长 F、d、C(可见光)预设。使用标准执行优化:具有四个环和六个臂的 RMS 波前质心,以及默认的空气边界约束(0 到 1000 毫米)。此外,该系统还受到远心和-4倍放大倍率的限制(在此显微镜设计中,图像是颠倒的)。
我选择这种显微镜设计是因为它相对容易设置并且具有实际应用。例如,机器视觉应用中通常需要远心性。我们始终保持优化简单,本文无意描述显微镜设计的一般情况。然而,本文的结果和结论适用于大多数具有共轭物体和像平面的成像系统,其中对衍射的大部分贡献发生在出瞳处,这意味着惠更斯点扩散函数 (PSF) 是评价系统性能的一个好参考。
多重结构设计
为了解决显微镜设计的分辨率问题,我们在物平面中创建了两个点源,并逐渐将它们分开,距离接近瑞利准则,并观察它们的 PSF 如何在图像平面中重叠。在显微镜设计中,瑞利准则 yRayleigh 可由下式计算:
其中 λPrimary 是主波长0.588 um,NA 是物镜的数值孔径0.2(本文不讨论聚光镜 NA)。虽然瑞利准则可以作为系统分辨率的衡量标准,但它假定一个完美的圆形、无畸变孔径光阑和非相干照明。此外,瑞利标准是一种主观度量,用于确定两个 PSF 的可辨别性,这实际上取决于观察者,以及需要从显微镜图像中检索的信息类型,我们将在本节的其余部分中看到。
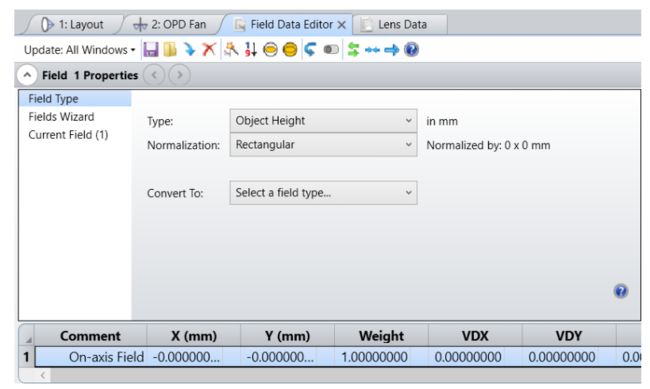
首先删除除轴上场(场1)以外的所有场,然后将其转换为象度,如图2所示。
图 2 - 用于分析显微镜分辨率的多配置方法的场设置。仅保留轴上视场,并且已将其转换为象度。
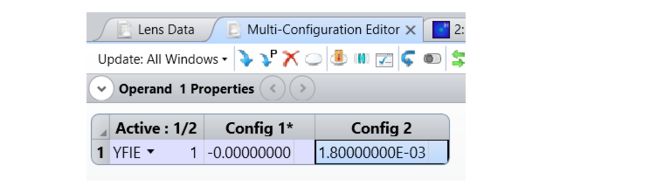
然后,使用单个 YFIE 操作数创建两个结构,并在第二个结构中指定值 1.8e-3 mm,如图3所示。
图 3 - PSF重叠分析的多重结构设置。两个点源在物平面上相距1.8 um。
最后,使用一个惠更斯 PSF 和惠更斯 PSF 截面来分析图像平面中两个 PSF 的重叠。两种分析可以对两种配置中的各个 PSF 进行相干求和(有关更多详细信息,请参阅帮助文件)。分析设置显示在图4中,特殊的多重结构设置显示为红色框和箭头(此选项不适用于 FFT PSF)。
图 4 - 惠更斯 PSF 设置。通过检查菜单栏中的所有配置,对各个 PSF 执行相干求和。
着重分析轴上场的分辨率上,但在各个视场的每个部分都可以进行相同的分析。
惠更斯 PSF 的结果如图5所示。
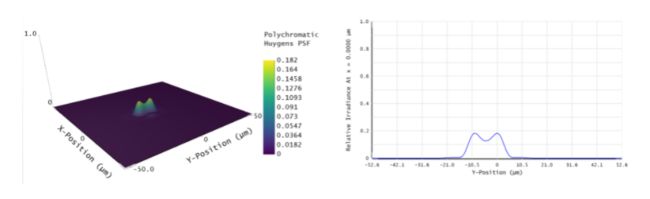
图 5 - 惠更斯 PSF 的结果,以及 PSF 截面与多重结构中1.8 um(瑞利准则)的物平面 Y 场分离重叠。在这种显微镜设计中,肉眼很难区分两个点光源。
可以看出,两个场点在图像平面上严重重叠,它们各自的 PSF 几乎无法区分。有两个原因可以解释这个结果。首先,通过执行 PSF 的相干求和,违反了瑞利准则的非相干照明假设,并导致分辨率下降。其次 OPD 扇形图显示出0.25波量级的像差,并且该显微镜位于衍射极限的边缘,这意味着它的衍射极限足以进行诸如惠更斯 PSF 之类的分析,但它仍然存在一些几何像差,这改变了系统的衍射极限性能。根据经验,最大化视野和分辨率的显微镜设计往往属于近衍射极限系统的类别,并且通常难以仅基于瑞利准则进行表征。
根据瑞利准则,可以增加场的分离距离,并重新评估结果。我们已经在图 6 中完成了它,在物平面中分离了2.3 um。
图 6 - 惠更斯 PSF 的结果,以及 PSF 截面与多重结构中2.3 um的物平面 Y 场分离。通过增加点之间的间隔距离,PSF 开始在图像平面中分离,并且可以观察到两个不同的峰值。
随着更大距离的分离,产生的 PSF 变得可区分。惠更斯 PSF 截面中的峰分离几乎10 um,这与系统放大倍数 (4X) 一致。当我们说“可区分”时,它是对我们在图 6 中看到的内容的定性评估。但是,如果定义了在后处理方面应如何分离峰,则可以使该标准更加客观。例如,一个标准可能是“我希望能够用80% 的阈值并检测两个独立的点”,在这种情况下,可以使用 OpticStudio 优化峰值间距以对应于最大相对辐照度的80% (这超出了本文的范围)。
最后,我们还可以考虑探测器的物理像素大小,以获得从显微镜看到的图像。PSF 的半高全宽约为12um,我们假设的探测器的物理像素大小为6.5 um,这显然违反了 Nyquist-Shanon 采样定理,这是显微镜设计的另一个限制。图7显示了当图像采样更改为32x32像素且图像增量(物理像素大小)为6.5 um时的惠更斯 PSF 结果。
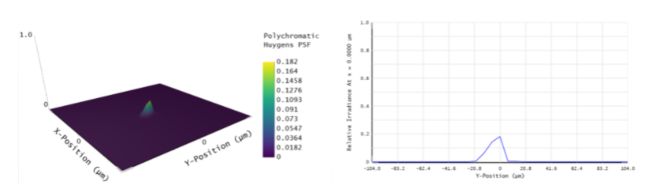
图 7 - 考虑探测器的物理像素大小时,PSF 重叠。像素太少导致 PSF 重叠并进一步降低显微镜的分辨率。
可以看出,物理像素尺寸不足进一步降低了显微镜的分辨率,虽然在图6中可以区分两个峰值,但它们现在在图7中再次重叠。在这种情况下,显微镜分辨率被称为像素受限,并且至少是放大倍数缩放的像素大小的两倍,即3.25 um(6.5除以4的两倍)。物平面中场之间3.25 um分离距离的结果如图8所示。
图 8 - 考虑到探测器的物理像素大小时,PSF重叠。3.25 um的分离使PSF再次分离。该距离对应于像素大小除以放大倍数的两倍,这是奈奎斯特-香农采样定理的结果。
考虑探测器像素大小,需要更大的分离以避免 PSF 混叠,并确保它至少由2个像素表示。3.25um的视场间隔与1.8 um瑞利标准大不相同,并且显示了分辨率的定义是多么模糊,但在本文中还没有考虑显微镜的公差,这将进一步降低该指标。
本节中介绍的方法考虑了两个相邻 PSF 的相干和,以及如何将它们彼此区分开来。虽然这种方法适用于相干成像系统,但对于非相干成像系统通常更为保守,并且可能导致性能过高的设计,这本身就成本更高。例如,在荧光显微镜中,分辨率是用荧光微珠测量的。从荧光微珠发出的光通常被认为是不相干的。在这种情况下,显微镜的性能有望更符合瑞利准则。
在下一节中,我将展示如何使用 OpticStudio 的图像模拟功能,通过非相干地对距离相近的点的 PSF 求和来研究非相干照明假设下显微镜设计的分辨率。
方法二:图像模拟(非相干成像)
对于这种方法,可以保留带有5个视场的原始显微镜设计,并将它们转换为象度(图 2)。在深入介绍图像模拟方法之前,我们想通知读者,本文不涉及OpticStudio 的这个功能的细节,我们假设你熟悉它,并且能够正确设置它。
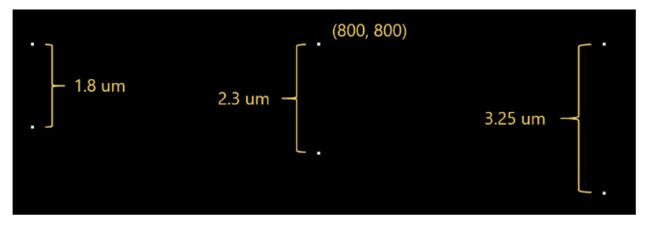
设置图像模拟的第一步是为其提供输入图像文件。由于图像模拟本质上是用这个输入图像执行显微镜 PSF 的卷积,我希望在我的输入图像中有多个冲击函数来模拟紧密分离的视场。换句话说,我的输入图像是一个完全黑色(零值像素)的背景,在每个字段的位置有一个白色(最大值)像素。像素的大小尽可能小,同时保持图像大小不要过大,这会导致合适的计算时间(以分钟为单位)。我选择表示图5-8中显示的惠更斯PSF面积的大约四倍,即400x400um2,这构成了固有限制。该区域随放大倍数缩放以对应于100x100um2的视场大小(请记住,放大倍数为4X)。我还选择我的图像大小为1600x1600像素,因此我的像素尺寸为0.0625x0.0625um2,远低于1.8 um的瑞利标准。我在我的图像中创建了六个白色像素,它们对应于两个近场的三种情况。这三种情况与第一种方法中分析的情况大致相同:分别为 1.8 (29)、2.3 (37) 和3.25 (52) um(像素)。包含白色像素的输入图像区域的放大图如图9所示,该图像可从文章附件 (PointSources.BMP) 中获得。
图 9 - 放大输入图像,显示六个白色像素对应于由 1.8 (29)、2.3 (37) 和3.25 (52) um(像素)分隔的三对点。横像间隔为6.25 (100) um(像素),避免了场对之间的重叠。上方的像素位于图像中的(800, 800)。
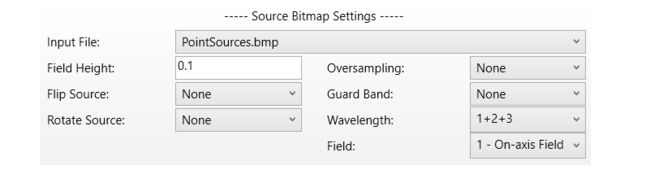
图像模拟的源位图设置如图10所示。
图 10 - 源位图的图像模拟设置。视场高度为100 um(镜头单位为0.1 mm),输入图像以同轴视场为中心。
视场高为100 um。对于这种方法,我们还将分析重点放在轴上场上,但也可以在不同的场位置进行相同的分析,我使用当前系统编辑器中定义的波长1到3的组合。
PSF 网格设置如图11所示。
图 11 - 左图:图像模拟功能的卷积网格设置。由于进行分析的区域受限,因此它在轴上使用单个 PSF。采样设置的选择与惠更斯 PSF 方法相同。像差设置为衍射。右图:生成的 PSF 网格,如图像模拟功能所示。
使用与惠更斯 PSF 方法相同的采样设置,并在轴上使用单个 PSF。这样做是因为视场高度为100um,这对应于我不希望 PSF 不会随着视场的一小部分改变发生太大的变化。图像模拟的结果如图12所示,默认探测器器和显示设置(全为零),计算这些结果可能需要几分钟时间。
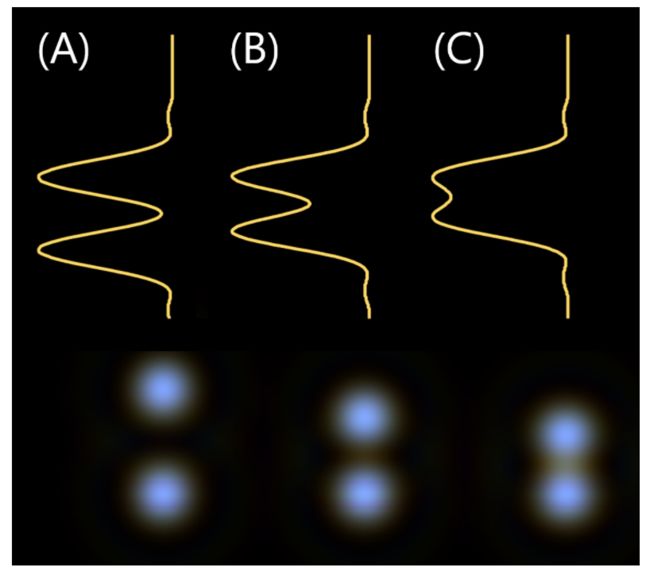
图 12 - 使用默认探测器和显示设置(全为零)的图像模拟结果。第一行描绘了穿过两个 PSF 的中心线的强度分布,第二行是 (A) 3.25、(B) 2.3 和 (C) 1.8 um 场之间的图像模拟输出。 由于显微镜的光学特性(负放大率),图像被反转。
从图 12 (C) 中,可以观察到1.8 um 的间隔(瑞利准则)下两个PSF可区分。强度有大约15%的小幅度下降,可用于使用阈值对图像进行后处理。场之间的距离越大,分离效果越好。与使用多重结构的 PSF 相干总和的惠更斯 PSF方法相比,结果在 PSF 的可分辨性方面更好。但是,我们还没有考虑探测器的物理尺寸。可以像图13那样调整图像模拟设置以考虑检测器特性。
图 13 - 考虑显微镜探测器物理尺寸时的探测器和显示设置。
考虑探测器物理特性的结果如图14所示,计算这些结果可能需要几分钟时间。
图 14 - 考虑显微镜探测器物理尺寸的图像模拟结果。即使在物平面中3.25 um的分离也不能分离 PSF。6.25um的横向间距使点对可区分。
紧密定位的点之间的分离不再可能,并且可以观察到,严格使用 Nyquist-Shanon 采样定理来确定像素限制分辨率通常是不够的。我们可能很幸运找到了图8的结果,而这些结果可能会出现混叠。在物平面中,点对之间的横向间隔为6.25 um(图 9),这使得这些场对之间的间隔干净利落。因此,我假设分辨率在3.25和6.25um之间。进一步的分析表明,5.125um的间隔可使物点的视觉、定性分离,如图15所示。
图 15 - 物平面中相距5.125um的一对点的图像模拟结果。两个较亮的像素似乎在强度上是可区分的。
再次强调,分辨率是一个随意的标准,最好从后处理需求的角度来定义它,但我希望说清楚设计的那些方面有助于分辨率,并且需要有一个明确的定义以确保对设计性能的正确评估,这也将有助于进行后续测试。再次强调,我没有讨论公差,这将进一步降低实际显微镜的性能。