机器学习面试题——传统算法
机器学习面试题——传统算法
提示:大厂笔试面试中,传统算法考察比较少,读者自行学习
傅里叶变换公式及其推导
边缘检测算法
牛顿法的推导过程
了解哪些插值算法
SIFT的整个详细流程
SIFT和SURF的区别
牛顿法和拟牛顿法
FFT和DFT的区别
双线性差值的操作过程
文章目录
- 机器学习面试题——传统算法
-
- @[TOC](文章目录)
- 傅里叶变换公式及其推导
- 边缘检测算法
- 牛顿法的推导过程
- 了解哪些插值算法
- SIFT的整个详细流程
- SIFT和SURF的区别
- 牛顿法和拟牛顿法
- FFT和DFT的区别
- 双线性差值的操作过程
- 总结
文章目录
- 机器学习面试题——传统算法
-
- @[TOC](文章目录)
- 傅里叶变换公式及其推导
- 边缘检测算法
- 牛顿法的推导过程
- 了解哪些插值算法
- SIFT的整个详细流程
- SIFT和SURF的区别
- 牛顿法和拟牛顿法
- FFT和DFT的区别
- 双线性差值的操作过程
- 总结
傅里叶变换公式及其推导
这东西,本科学信号与系统,学数字信号处理,玩得666了
傅里叶变换公式:这里我们用 [公式] 表示频率。

傅里叶反变换公式:
 下面两者称为傅里叶变换对,可以相互转换:
下面两者称为傅里叶变换对,可以相互转换:
![]()
边缘检测算法
边缘一般是指图像在某一局部强度剧烈变化的区域。强度变化一般有两种情况:
(1)阶跃变化:此图对应的是向亮渐变的过程。

(2)屋顶变化:灰度变化图像如下图所示(横轴表示空间变化,纵轴表示灰度变化,虚线表示边缘):对应得实由暗到亮再变暗的过程。

边缘检测的任务:找到具有阶跃变化或者屋顶变化的像素点的集合。
边缘检测基本原理:既然边缘是灰度变化最剧烈的位置,最直观的想法就是求微分。
对于第一种情况:一阶微分的峰值为边缘点,二阶微分的零点为边缘点。
对于第二种情况:一阶微分的零点为边缘点,二阶微分的峰值为边缘点。
(3)sobel算子:
考虑到了相邻不同像素点的影响程度是不同的,所以采用加权平均。其卷积模板如下:
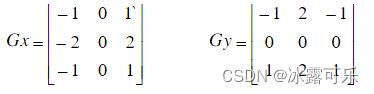
(4)canny:canny算子是一种求最优边缘检测的一套方法。是一种先平滑再求导的方法。
第一步:对图像用高斯滤波器进行平滑处理。
高斯滤波用于对图像进行减噪,采用邻域加权平均的方法计算每一个像素点的值。
第二步:利用一阶差分计算边缘的方向与幅值。

第三步:非极大值抑制。
仅仅求出全局的梯度方向并不能确定边缘的位置。所以需要对一些梯度值不是最大的店进行抑制,突出真正的边缘。
(5)laplace:laplacian算子是一些使用二阶微分的算子,实际上就是梯度的散度:

牛顿法的推导过程
逻辑斯蒂回归可以使用梯度下降法和牛顿法来求解对数似然函数的最优化问题,
从实例中我们也能发现牛顿法的收敛速度远快于梯度下降法

了解哪些插值算法
(1)最近邻插值法(Nearest Neighbour Interpolation):选取距离插入的像素点(x+u, y+v)最近的一个像素点,用它的像素点的灰度值代替插入的像素点。
最近邻插值法虽然计算量较小,但可能会造成插值生成的图像灰度上的不连续,在灰度变化的地方可能出现明显的锯齿状。
(2)**双线性插值:**双线性内插法的计算比最邻近点法复杂,计算量较大,但没有灰度不连续的缺点,结果基本令人满意。
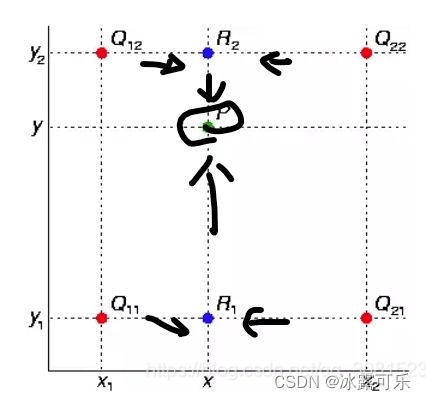
它具有低通滤波性质,使高频分量受损,图像轮廓可能会有一点模糊。
(3)双三次插值:三次多项式插值法插值精度高,具有更EI平滑的边缘,图像损失质量低,但是计算量较大。
SIFT的整个详细流程
SIFT算法的实质是在不同的尺度空间上查找关键点(特征点),并计算出关键点的方向。
SIFT所查找到的关键点是一些十分突出,不会因光照,仿射变换和噪音等因素而变化的点,如角点、边缘点、暗区的亮点及亮区的暗点等。
目标检测中的算法——检测关键点
SIFT算法分解为如下四步:
(1)尺度空间极值检测:搜索所有尺度上的图像位置。通过高斯微分函数来识别潜在的对于尺度和旋转不变的兴趣点。
(2)**关键点定位:**在每个候选的位置上,通过一个拟合精细的模型来确定位置和尺度。关键点的选择依据于它们的稳定程度。
(3)**方向确定:**基于图像局部的梯度方向,分配给每个关键点位置一个或多个方向。所有后面的对图像数据的操作都相对于关键点的方向、尺度和位置进行变换,从而提供对于这些变换的不变性。
(4)**关键点描述:**在每个关键点周围的邻域内,在选定的尺度上测量图像局部的梯度。这些梯度被变换成一种表示,这种表示允许比较大的局部形状的变形和光照变化。
SIFT和SURF的区别
SURF是在SIFT的基础上改进而生,不仅提高了计算速度,而且更加安全鲁棒性,两者的实现原理很相似。
(1)构建图像金字塔:SIFT特征利用不同尺寸的图像与高斯差分滤波器卷积;SURF特征利用原图片与不同尺寸的方框滤波器卷积。
(2)特征描述子:SIFT特征有4×4×8=128维描述子,SURF特征有4×4×4=64维描述子
(3)特征点检测方法:SIFT特征先进行非极大抑制,再去除低对比度的点,再通过Hessian矩阵去除边缘响应过大的点;SURF特征先利用Hessian矩阵确定候选点,然后进行非极大抑制
(5)特征点主方向:SIFT特征在正方形区域内统计梯度幅值的直方图,直方图最大值对应主方向,可以有多个主方向;SURF特征在圆形区域内计算各个扇形范围内x、y方向的haar小波响应,模最大的扇形方向作为主方向
牛顿法和拟牛顿法
牛顿法可由二阶泰勒展开求导可近似得到牛顿法迭代公式:

但是在实际应用过程中,我们会发现海塞矩阵的逆矩阵往往计算比较复杂,于是又有了拟牛顿法来简化这一过程。
在拟牛顿法中,考虑优化出一个n阶矩阵D来代替海塞矩阵的逆矩阵。
可以发现海塞矩阵逆矩阵的近似矩阵D(x)的选择条件比较灵活,可以有多种具体的实现方法。比较常用的算法是DFP算法替代海塞矩阵逆矩阵的迭代公式
FFT和DFT的区别
FFT是一种DFT的高效算法,称为快速傅立叶变换(fast Fourier transform)。
傅里叶变换是时域一频域变换分析中最基本的方法之一。
在数字信号处理领域应用的离散傅里叶变换(DFT:Discrete Fourier Transform)是许多数字信号处理方法的基础
FFT在DFT的基础上减少了很多次乘法,真正使得DFT在计算机中得到了应用。
双线性差值的操作过程
**双线性插值:**双线性内插法的计算比最邻近点法复杂,计算量较大,但没有灰度不连续的缺点,结果基本令人满意。


它具有低通滤波性质,使高频分量受损,图像轮廓可能会有一点模糊。
总结
提示:重要经验:
1)很多都是图像处理领域的传统算法,应用于目标检测,目标跟踪,数字信号处理等
2)这些基础八股文,简单地了解一下,有个印象,不少东西是课堂上学过的,回忆一下就行。