阿白数模笔记之最小二乘法（Least square method）
目录
简介
参数矩阵的解
MATLAB代码详解
①样本维度为1
②样本维度为2
③样本维度大于2
简介
记录有m*n（m个样本，n个维度）的实测数据
，对应1*n的实际值
，若要进行线性拟合，即找到1*n的参数矩阵
使得
参数矩阵的解
参数矩阵满足 
。从数据角度思考：①补充常数项更加合理，线性拟合效果更好即参数矩阵为1*(n+1)型，方程满足
将实测数据改为m*(n+1)型第一列全为1，仍然有矩阵方程。②矩阵方程有解的充要条件是
，即的张子空间。实际应用中未必有解，因此寻求近似最优解，引入最小二乘法。
，对求偏导，得
，解得
。（这里仍然有
是否奇异的问题，奇异时即样本变量之间存在近似线性相关关系（复共线性）有其他方法解决，作者之后的文章会涉及，此处以为非奇异矩阵）。
MATLAB代码详解
①样本维度为1
先判定Y与X线性相关性。
load('population.mat')
x=p(:,2);y=p(:,5);
co=corrcoef([x,y])
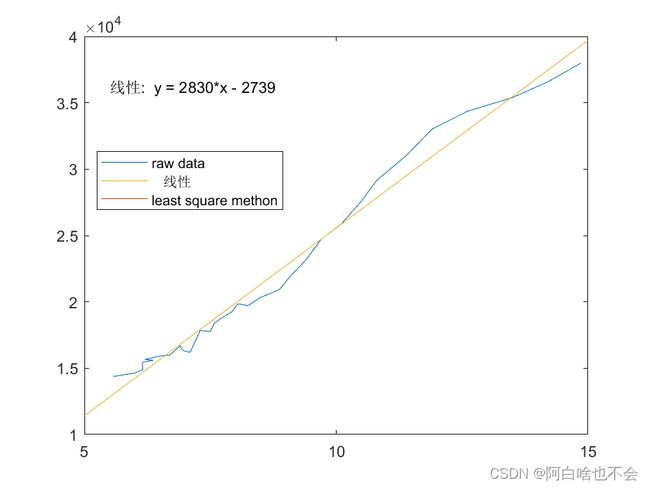
plot(x,y);
legend('raw data','location','northwest')
co =
1.0000 0.9925
0.9925 1.0000
计算参数矩阵并绘制图形
x1=[ones(size(x)),x];
theta=(x1'*x1)^(-1)*x1'*y
xdata=[min(x),max(x)];
ydata=xdata*theta(2)+theta(1);
hold on
plot(xdata,ydata)
legend('raw data','least square methon','location','northwest')
theta =
1.0e+03 *
-2.7394
2.8302检验：figure界面的工具一栏有基本拟合选项，选取线性拟合即可发现所得曲线与上面绘制的重合
②样本维度为2
不再赘述，直接上代码
x1=p(:,4);x2=p(:,5);y=p(:,2);
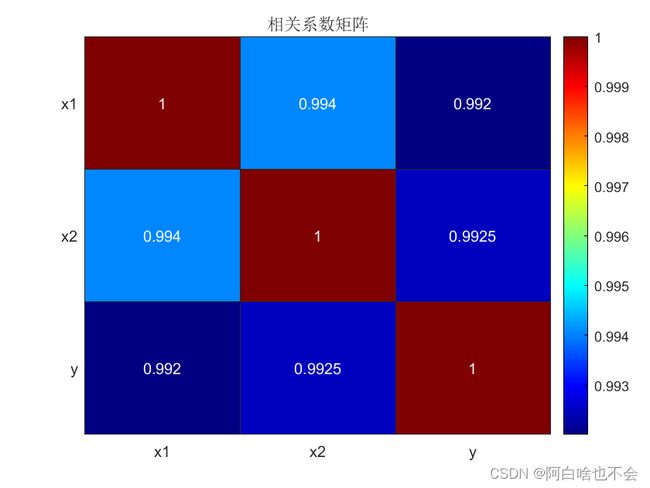
heatmap({'x1','x2','y'},{'x1','x2','y'},corrcoef([x1,x2,y]),'Title','相关系数矩阵');
colormap('jet');
plot3(x1,x2,y,'LineWidth',2);grid on
x=[ones(size(x1)),x1,x2];
theta=(x'*x)^(-1)*x'*y
yfit=theta(1)+theta(2)*x1+theta(3)*x2;
hold on
plot3(x1,x2,yfit,'LineWidth',2)
legend('raw data','least square methon')
theta =
3.3518
0.0000
0.0002③样本维度大于2
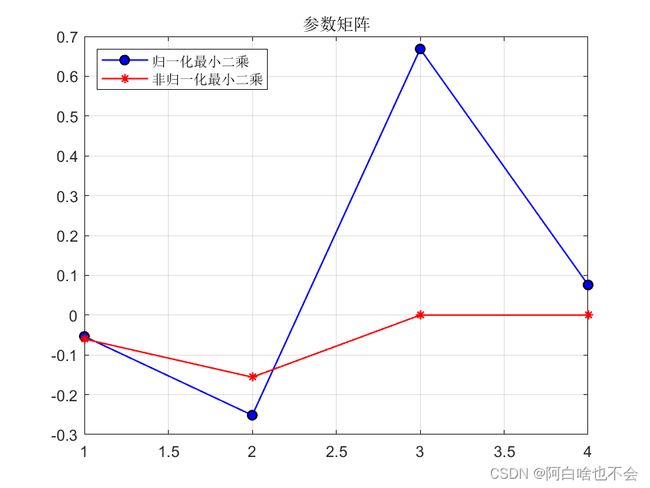
从②发现theta(2)，theta(3)都接近0，这并不是因为相关系数低，而是数量级的差距，通过数据归一化可以解决这一问题。
heatmap(corrcoef(p),'Title','相关系数矩阵');
colormap('jet')
figure
%归一化最小二乘
h1=mapminmax(p(:,2)',0,1)';
x10=ones(size(p,1),1);
X1=[x10,mapminmax(p(:,[1,3,4,5])',0,1)'];
theta1=(X1'*X1)^(-1)*X1'*h1;
plot(theta1(2:5),'bo-','LineWidth',1,'MarkerEdgeColor','k','MarkerFaceColor','b')
hold on
%非归一化最小二乘
h=p(:,2);
x20=ones(size(p,1),1);
X2=[x20,p(:,[1,3,4,5])];
theta2=(X2'*X2)^(-1)*X2'*h;
plot(theta2(2:5),'r*-','LineWidth',1,'MarkerEdgeColor','r','MarkerFaceColor','r')
title('参数矩阵')
legend('归一化最小二乘','非归一化最小二乘','Location','northwest');grid on
set(gca,'ytick',-0.3:0.1:0.7)