路径 Floyd 蓝桥杯 JAVA

题目描述：

小蓝学习了最短路径之后特别高兴，他定义了一个特别的图，希望找到图中的最短路径。 小蓝的图由2021 个结点组成，依次编号1 至2021。
对于两个不同的结点a, b，如果a 和b 的差的绝对值大于21，则两个结点之间没有边相连； 如果a 和b
的差的绝对值小于等于21，则两个点之间有一条长度为a 和b 的最小公倍数的无向边相连。 例如：结点1 和结点23 之间没有边相连；结点3
和结点24 之间有一条无向边，长度为24； 结点15 和结点25 之间有一条无向边，长度为75。 请计算，结点1 和结点2021
之间的最短路径长度是多少。

提示：建议使用计算机编程解决问题

1.Floyd算法讲解

---

Floyd算法：

Floyd算法又称为插点法,是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法,与Dijkstra算法类似。

大致过程：

以下面的有向图为例：

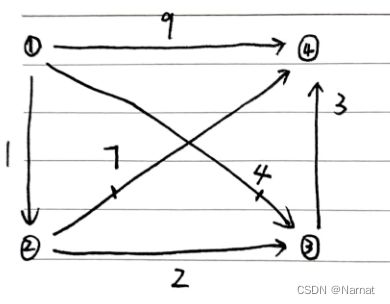
1.建立一个 5 * 5 数组graph用于储存两点间的初始路径，其中graph[i][j] = k,表示图中点 i 到点 j 的路径长度为 k

2.输入初始值
graph[1][1] = 0, graph[1][2] = 1, graph[2][4] = 7
graph[2][2] = 0, graph[1][3] = 4, graph[3][4] = 3
graph[3][3] = 0, graph[1][4] = 9
graph[4][4] = 0, graph[2][3] = 2
剩下的距离都是无穷远省略，例如由图可知：graph[2][1] = ∞

生成的数组如下图所示：

上图只是基本路径并不是最短路径，以点1 到点4 为例：

可以看出点 1直达点 4，是没有中间经过"中转站"再达到点4的路程短。

floyd算法找最短路径的核心就是寻找这些中转站，使得两点间的路径更可能短

3.找中转站
为了不遗漏所有可能的”中转点“，floyd算法试着将所有点都作为中转点挨个遍历（这需要一个for循环）。

4.利用floyd算法，查找点1到点4最短路径具体过程，代码如下如下：
（其中点1 ~ 4分别做中转站运行的结果，在代码里我都打印出来了，直接运行代码就可以看，为了方便观赏INF = 1111代表两点间没有路径）

public class Main {
 static int[][] graph = new int[5][5];
 static final int INF = 1111;
 
 private static void floyd() {
  for (int k = 1; k <= 4; k++) {
   for (int i = 1; i <= 4; i++) {
    for (int j = 1; j <= 4; j++) {
     if (i != j && graph[i][j] > graph[i][k] + graph[k][j]) {
      graph[i][j] = graph[i][k] + graph[k][j];
     }
    }
   }
   print();//打印
  }
 }
 
 public static void print() {
	 for(int i = 1; i <= 4; i ++) {
		  for(int j = 1; j <= 4; j ++) {
			  System.out.print(graph[i][j] + " ");
		  }
		  System.out.println();
	  }
	 System.out.println();
 }
 
 public static void main(String[] args) {
  for (int i = 1; i <= 4; i++) {
   for (int j = 1; j <= 4; j++) {
    graph[i][j] = INF;
   }
  }
  for(int i = 1; i <= 4; i ++)
	  for(int j = 1; j <= 4; j ++)
		  if(i == j)
			  graph[i][j] = 0;
  graph[1][2] = 1;
  graph[1][4] = 9;
  graph[1][3] = 4;
  
  graph[2][4] = 7;
  graph[2][3] = 2;
  graph[3][4] = 3;
  for(int i = 1; i <= 4; i ++) {
	  for(int j = 1; j <= 4; j ++) {
		  System.out.print(graph[i][j] + " ");
	  }
	  System.out.println();
  }
  System.out.println();
  floyd();
  
  System.out.println(graph[1][4]);//最短路径
 }
 
}

Floyd算法
优点：代码少
缺点：慢

---

2.输出最优路径

要想输出具体的路径，可以再设立一个path数组，其中path[i][j] = w, 代表点 i 和点 j 之间的中转站为 w，path[i][j]的初始值为 - 1，代表i, j之间没有路径。
输出具体路径的代码如下：

 public static void printpath(int u, int v) {
	 if(path[u][v] == -1)
		 System.out.print("<" + u + "," + v + ">");
	 else {
		 int mid = path[u][v];
		 printpath(u, mid);
		 printpath(mid, v);
	 }
 }

以上图为例完整代码如下：

public class Main {
 static int[][] graph = new int[5][5];
 static final int INF = 1111;
 public static int path[][] = new int[5][5];
 
 private static void floyd() {
  for (int k = 1; k <= 4; k++) {
   for (int i = 1; i <= 4; i++) {
    for (int j = 1; j <= 4; j++) {
     if (i != j && graph[i][j] > graph[i][k] + graph[k][j]) {
      graph[i][j] = graph[i][k] + graph[k][j];
      path[i][j] = k;
     }
    }
   }
   print();
  }
 }
 
 public static void print() {
	 for(int i = 1; i <= 4; i ++) {
		  for(int j = 1; j <= 4; j ++) {
			  System.out.print(graph[i][j] + " ");
		  }
		  System.out.println();
	  }
	 System.out.println();
 }
 
 public static void main(String[] args) {
  for (int i = 1; i <= 4; i++) {
   for (int j = 1; j <= 4; j++) {
    graph[i][j] = INF;
    path[i][j] = -1;
   }
  }
  for(int i = 1; i <= 4; i ++)
	  for(int j = 1; j <= 4; j ++)
		  if(i == j)
			  graph[i][j] = 0;
  graph[1][2] = 1;
  graph[1][4] = 9;
  graph[1][3] = 4;
  
  graph[2][4] = 7;
  graph[2][3] = 2;
  graph[3][4] = 3;
  for(int i = 1; i <= 4; i ++) {
	  for(int j = 1; j <= 4; j ++) {
		  System.out.print(graph[i][j] + " ");
	  }
	  System.out.println();
  }
  System.out.println();
  floyd();
  
  printpath(1, 4);
  System.out.println("\n");
  
  System.out.println(graph[1][4]); // 10266837
 }
 
 public static void printpath(int u, int v) {
	 if(path[u][v] == -1)
		 System.out.print("<" + u + "," + v + ">");
	 else {
		 int mid = path[u][v];
		 printpath(u, mid);
		 printpath(mid, v);
	 }
 }
}

---

3.本题代码

解题思路：

了解floyd后解决本题就非常简单了。

1.设置graph数组为大小2100 * 2100
2.若两点i, j差的绝对值小于等于21，那么求出i, j最小公倍数，就为graph[i][j]的值，否者就是没有路径，设为无穷大
3.利用floyd算法求最短路径，输出1 ~ 2021的路径即可

求两数间的最小公倍数代码如下：

public static int getmingb(int a, int b) {//求最小公倍数
	if(a == b)
		return 0;
	int min = Math.min(a, b);
	int maxgb = 1;
	for(int i = 1; i <= min; i ++)
		if(a % i == 0 && b % i == 0) maxgb = i;
	return a * b / maxgb;
}

即以1 和 两数中最小的那个数为遍历区间，遍历找到最大公约数并储存。两数相乘再除掉最小公约数，就是最小公倍数。

本题完整代码如下：
由于Floyd采用的是三重 for 循环，再加上寻找最小公倍数算法的一个 for 循环和初始化的两重循环，所以计算机大概的执行次数为 2000 ^ 3 + 2000^3 大概是16*10^9,由于计算机 1s 运行 10^9 次，所以计算机执行完整个程序大概要16s

import java.util.*;
public class Main {
	public static Integer INF = 0x3f3f3f3f;
	public static int graph[][] = new int[2100][2100];
	
	public static void main(String[] args){
        for(int i = 1; i <= 2021; i ++)
        	for(int j = 1; j <= 2021; j ++) {
        		if(graph[i][j] == 0) {
        			if(Math.abs(i - j) <= 21) {
        				graph[i][j] = getmingb(i, j);
        				graph[j][i] = graph[i][j];
        			}
        			else graph[i][j] = INF;
        		}
        	}
        
        Floyd();
        System.out.print(graph[1][2021]);
	}
public static void Floyd() {//弗洛伊德算法
	for(int k = 1; k <= 2021; k ++) {
		for(int i = 1; i <= 2021; i ++)
			for(int j = 1; j <= 2021; j ++) {
				if(i != j && graph[i][j] > graph[i][k] + graph[k][j])
					graph[i][j] = graph[i][k] + graph[k][j];
			}
	}
}
public static int getmingb(int a, int b) {//求最小公倍数
	if(a == b)//graph[1][1] = 0
		return 0;
	int min = Math.min(a, b);
	int maxgb = 1;
	for(int i = 1; i <= min; i ++)
		if(a % i == 0 && b % i == 0) maxgb = i;
	return a * b / maxgb;
}
}