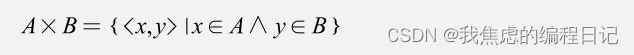【离散数学】二元关系

一、有序对和笛卡尔积

有序对：形如的序偶称为有序对，其中x为其第一个元素，y为其第二个元素。

笛卡尔积：将两个集合A、B中的所有元素相互排列组合形成的集合称为集合A和B的笛卡尔积。

笛卡尔积的性质：

不满足交换律和结合律，只满足分配律。

因为序偶是有序存在的，第一个元素和第二个元素变换位置后与之前是不相等的。

二、二元关系

二元关系：一个集合要么是空集，要么不是空集，但是每个元素都是有序对的集合是二元关系。

特殊关系：空关系、全域关系(E)、恒等关系(I)。

关系的表示方法：

集合表达式、关系图、关系矩阵。

三、关系的运算

设R是二元关系，则：

1.定义域：第一个元素的集合

2.值域：第二个元素的集合

3.域：定义域和值域的并集

4.逆关系：是把原来有序对的顺序全部交换，例如：换为

5.合成关系：将两个集合中，两两首尾相等的元素进行合并得到新的序偶，并将这些序偶集合起来变成一个新的关系。例如：  --->  此时的即为合成后的关系。

四、关系的性质

1.常考性质

自反性：集合中每个元素都出现一次，出现时是以相等关系出现

反自反性：集合中没有相等关系

对称性：集合中每一个都有

反对称性：集合中没有一个有

传递性：每一个和都能找到，如果没有能形成传递性的序偶，也具有传递性，因为这是一个蕴含表达式。

2.关系的闭包

自反闭包(r(R))：给原集合并上相等集合

对称闭包(s(R))：给原籍和并上逆反集合

传递闭包(t(R))：给原集合并上原集合的原集合的幂集，至多到元素次幂。