隐马尔科夫模型HMM之前后向算法Python代码实现,包括2个优化版本
☕️ 本文系列文章汇总:
(1)HMM开篇:基本概念和几个要素
(2)HMM计算问题:前后向算法
(3)HMM学习问题:Baum-Welch算法
(4) HMM预测问题:维特比算法本篇算法原理分析及公式推导请参考: HMM计算问题:前后向算法
之前发布的四篇隐马尔科夫模型系列学习博文,将隐马尔科夫模型包含的各个算法的原理及公式都详细介绍了,所谓无代码实现无以成体系,那么接下来我会带大家把算法用代码实现一遍,语言主要为python。本篇先来对前后向算法进行coding~
1. 参数初始化:
"""
初始化模型参数
:param pi: 初始状态概率向量
:param A: 已学习得到的状态转移概率矩阵,这里直接引用课本中的例子10.2
:param B: 已学习得到的概率矩阵,这里直接引用课本中的例子10.2
:param V: 已知的观测集合,同样使用例子中的值
"""
self.pi = pi
self.A = A
self.B = B
self.V = V2. 根据原理公式,定义前向算法计算过程:
def forward(self, O):
"""
前向算法
:param O: 已知的观测序列
:return: P(O|λ)
"""
row, col = len(O), self.A.shape[0]
alpha_t_plus_1 = np.zeros((row, col), dtype=float)
for t, o in enumerate(O):
if t == 0:
# 初值α 公式10.15
for i, p in enumerate(self.pi):
obj_index = self.V.index(o)
alpha_t_plus_1[t][i] = p * self.B[i][obj_index]
else:
# 递推 公式10.16
for i in range(self.A.shape[0]):
alpha_ji = 0.
# 公式10.16里中括号的内容
for j, a in enumerate(alpha_t_plus_1[t-1]):
alpha_ji += (a * self.A[j][i])
obj_index = self.V.index(o)
# 公式10.16
alpha_t_plus_1[t][i] = alpha_ji * self.B[i][obj_index]
return alpha_t_plus_1该方法主要输出的是前向算法中alpha的中间结果,即原理中提到的![]() 。
。
3. 定义后向算法计算过程:
def backward(self, O):
"""
后向算法
:param O: 已知的观测序列
:return: P(O|λ)
"""
row, col = len(O), self.A.shape[0]
betaT = np.zeros((row+1, col), dtype=float)
for t, o in enumerate(O[::-1]):
if t == 0:
# 初值β 公式10.19
betaT[t][:] = [1] * self.A.shape[0]
continue
else:
# 反向递推 公式10.20
for i in range(self.A.shape[0]):
beta_t = 0.
obj_index = self.V.index(O[t - 1])
for j, b in enumerate(betaT[t-1]):
beta_t += (self.A[i][j] * self.B[j][obj_index] * b)
betaT[t][i] = beta_t
betaT[-1][:] = [self.pi[i] * self.B[i][self.V.index(O[0])] * betaT[-2][i] for i in range(self.A.shape[0])]
return betaT 该方法主要输出的是前向算法中beta的中间结果,即原理中提到的![]() 。
。
4. 定义概率计算函数:
def cal_prob(self, O, opt):
if opt == 'f':
metrix = self.forward(O)
# 计算前向算法P(O|λ) 公式10.17
return sum(metrix[-1])
elif opt == 'b':
# 计算后向算法P(O|λ) 公式10.21
metrix = self.backward(O)
return sum(metrix[-1])将上述方法封装成一个类:
import numpy as np
class FB:
def __init__(self, pi, A, B, V):
"""
初始化模型参数
:param pi: 初始状态概率向量
:param A: 已学习得到的状态转移概率矩阵,这里直接引用课本中的例子10.2
:param B: 已学习得到的概率矩阵,这里直接引用课本中的例子10.2
:param V: 已知的观测集合,同样使用例子中的值
"""
self.pi = pi
self.A = A
self.B = B
self.V = V
def cal_prob(self, O, opt):
if opt == 'f':
metrix = self.forward(O)
# 计算P(O|λ) 公式10.17
return sum(metrix[-1])
elif opt == 'b':
# 计算P(O|λ) 公式10.21
metrix = self.backward(O)
return sum(metrix[-1])
def forward(self, O):
"""
前向算法
:param O: 已知的观测序列
:return: P(O|λ)
"""
row, col = len(O), self.A.shape[0]
alpha_t_plus_1 = np.zeros((row, col), dtype=float)
for t, o in enumerate(O):
if t == 0:
# 初值α 公式10.15
for i, p in enumerate(self.pi):
obj_index = self.V.index(o)
alpha_t_plus_1[t][i] = p * self.B[i][obj_index]
else:
# 递推 公式10.16
for i in range(self.A.shape[0]):
alpha_ji = 0.
# 公式10.16里中括号的内容
for j, a in enumerate(alpha_t_plus_1[t-1]):
alpha_ji += (a * self.A[j][i])
obj_index = self.V.index(o)
# 公式10.16
alpha_t_plus_1[t][i] = alpha_ji * self.B[i][obj_index]
return alpha_t_plus_1
def backward(self, O):
"""
后向算法
:param O: 已知的观测序列
:return: P(O|λ)
"""
row, col = len(O), self.A.shape[0]
betaT = np.zeros((row+1, col), dtype=float)
for t, o in enumerate(O[::-1]):
if t == 0:
# 初值β 公式10.19
betaT[t][:] = [1] * self.A.shape[0]
continue
else:
# 反向递推 公式10.20
for i in range(self.A.shape[0]):
beta_t = 0.
obj_index = self.V.index(O[t - 1])
for j, b in enumerate(betaT[t-1]):
beta_t += (self.A[i][j] * self.B[j][obj_index] * b)
betaT[t][i] = beta_t
betaT[-1][:] = [self.pi[i] * self.B[i][self.V.index(O[0])] * betaT[-2][i] for i in range(self.A.shape[0])]
return betaT用书上的例子运行一下:
if __name__ == '__main__':
from time import time
# 课本例子10.2
pi = [0.2, 0.4, 0.4]
a = np.array([
[0.5, 0.2, 0.3],
[0.3, 0.5, 0.2],
[0.2, 0.3, 0.5]
])
b = np.array([
[0.5, 0.5],
[0.4, 0.6],
[0.7, 0.3]
])
O = ['红', '白', '红']
f = FB(pi=pi, A=a, B=b, V=['红', '白'])
# start = time()
resf = f.forward(O)
resb = f.backward(O)
# print(time()-start)
print('α:{}\n前向算法的概率计算结果:{}'.format(resf, f.cal_prob(O, opt='f')))
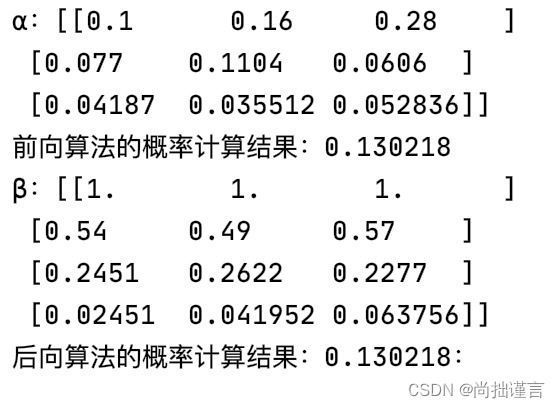
print('β:{}\n后向算法的概率计算结果:{}:'.format(resb, f.cal_prob(O, opt='b')))运行结果:
另外我们注意到上面的代码中,嵌套了三层for循环,当数据量很大的时候,这样计算很耗时,那么我们来优化一下:
优化版一:
我们注意到,内层for循环主要是为了矩阵计算的,所以我们其实可以直接利用numpy来进行矩阵的运算。
import numpy as np
class FB:
def __init__(self, pi, A, B, V):
"""
初始化模型参数
:param pi: 初始状态概率向量
:param A: 已学习得到的状态转移概率矩阵,这里直接引用课本中的例子10.2
:param B: 已学习得到的概率矩阵,这里直接引用课本中的例子10.2
:param V: 已知的观测集合,同样使用例子中的值
"""
self.pi = np.array(pi)
self.A = np.array(A)
self.B = np.array(B)
self.V = V
def cal_prob(self, O, opt):
if opt == 'f':
metrix = self.forward(O)
# 计算P(O|λ) 公式10.17
return sum(metrix[-1])
elif opt == 'b':
# 计算P(O|λ) 公式10.21
metrix = self.backward(O)
return sum(metrix[-1])
def forward(self, O):
"""
前向算法
:param O: 已知的观测序列
:return: P(O|λ)
"""
row, col = len(O), self.A.shape[0]
alpha_t_plus_1 = np.zeros((row, col), dtype=float)
obj_index = self.V.index(O[0])
# 初值α 公式10.15
alpha_t_plus_1[0][:] = self.pi * self.B[:].T[obj_index]
for t, o in enumerate(O[1:]):
t += 1
# 递推 公式10.16
obj_index = self.V.index(o)
for i in range(self.A.shape[0]):
# 公式10.16
alpha_ji = alpha_t_plus_1[t-1][:] @ self.A[:].T[i]
alpha_t_plus_1[t][i] = alpha_ji * self.B[i][obj_index]
return alpha_t_plus_1
def backward(self, O):
"""
后向算法
:param O: 已知的观测序列
:return: P(O|λ)
"""
row, col = len(O), self.A.shape[0]
betaT = np.zeros((row+1, col), dtype=float)
# 初值β 公式10.19
betaT[0][:] = [1] * self.A.shape[0]
for t, o in enumerate(O[::-1][1:]):
t += 1
# 反向递推 公式10.20
obj_index = self.V.index(O[t-1])
for i in range(self.A.shape[0]):
beta_t = self.A[i][:] * self.B[:].T[obj_index] @ betaT[t-1][:].T
betaT[t][i] = beta_t
betaT[-1][:] = [self.pi[i] * self.B[i][self.V.index(O[0])] * betaT[-2][i] for i in range(self.A.shape[0])]
return betaT优化版二:
优化版一中,只省略了最内层循环,即每个状态的每一列。其实近一步观察发现,对于每一行的for循环也可以直接用矩阵计算的方式省略
import numpy as np
class FB:
def __init__(self, pi, A, B, V):
"""
初始化模型参数
:param pi: 初始状态概率向量
:param A: 已学习得到的状态转移概率矩阵,这里直接引用课本中的例子10.2
:param B: 已学习得到的概率矩阵,这里直接引用课本中的例子10.2
:param V: 已知的观测集合,同样使用例子中的值
"""
self.pi = np.array(pi)
self.A = np.array(A)
self.B = np.array(B)
self.V = V
def cal_prob(self, O, opt):
if opt == 'f':
metrix = self.forward(O)
# 计算P(O|λ) 公式10.17
return sum(metrix[-1])
elif opt == 'b':
# 计算P(O|λ) 公式10.21
metrix = self.backward(O)
return sum(metrix[-1])
def forward(self, O):
"""
前向算法
:param O: 已知的观测序列
:return: P(O|λ)
"""
row, col = len(O), self.A.shape[0]
alpha_t_plus_1 = np.zeros((row, col), dtype=float)
obj_index = self.V.index(O[0])
# 初值α 公式10.15
alpha_t_plus_1[0][:] = self.pi * self.B[:].T[obj_index]
for t, o in enumerate(O[1:]):
t += 1
# 递推 公式10.16
obj_index = self.V.index(o)
alpha_ji = alpha_t_plus_1[t - 1][:].T @ self.A
alpha_t_plus_1[t][:] = alpha_ji * self.B[:].T[obj_index]
return alpha_t_plus_1
def backward(self, O):
"""
后向算法
:param O: 已知的观测序列
:return: P(O|λ)
"""
row, col = len(O), self.A.shape[0]
betaT = np.zeros((row+1, col), dtype=float)
# 初值β 公式10.19
betaT[0][:] = [1] * self.A.shape[0]
for t, o in enumerate(O[::-1][1:]):
t += 1
# 反向递推 公式10.20
obj_index = self.V.index(O[t-1])
beta_t = self.A * self.B[:].T[obj_index] @ betaT[t-1][:].T
betaT[t][:] = beta_t
betaT[-1][:] = [self.pi[i] * self.B[i][self.V.index(O[0])] * betaT[-2][i] for i in range(self.A.shape[0])]
return betaT好啦,就是这么一步步递进优化,方法论就是,先用基本的代码将原理实现,帮助理解,然后发现竟然有3个for循环,复杂度且不说,代码首先就不美观,看看有没有可以优化的地方,发现for循环的服务对象是矩阵计算,所以,很自然的想到直接利用矩阵计算的方法一步到位。代码已经放到GitHub上了,我将会持续更新其它算法的实现。