数据结构之最大堆
文章目录
-
- C++数据结构之最大堆
-
- 堆的原理精讲
- 在数组中快速创建堆
- 插入新元素and堆顶元素出列
- 优先队列
- 堆排序
C++数据结构之最大堆
堆的原理精讲
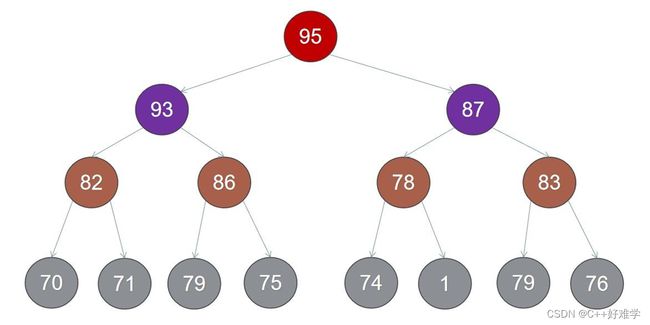
最大堆特点:
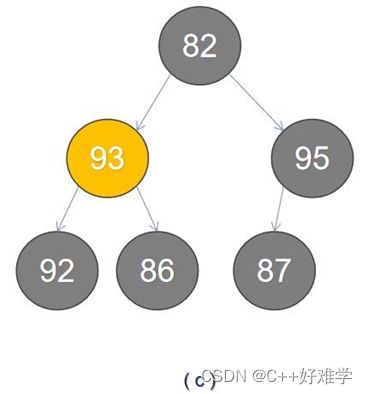
看图识最大堆:
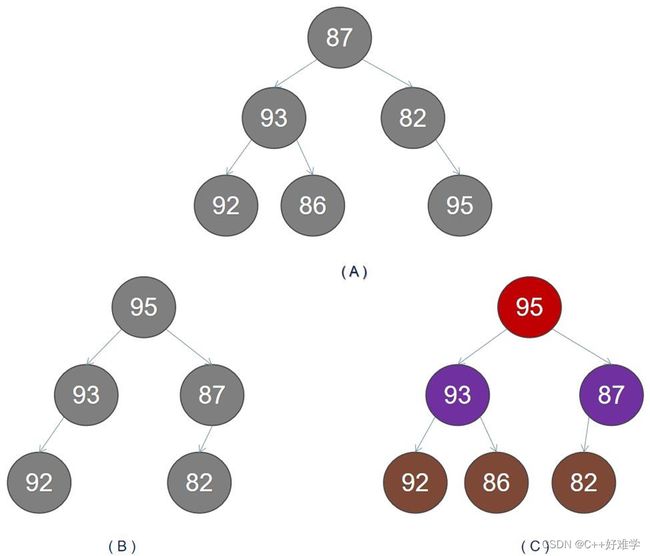
A B 不是堆,C 是最大堆
堆是你见过的最有个性的树!它是用数组表示的树
在数组中快速创建堆
初始状态:
第一步:
-
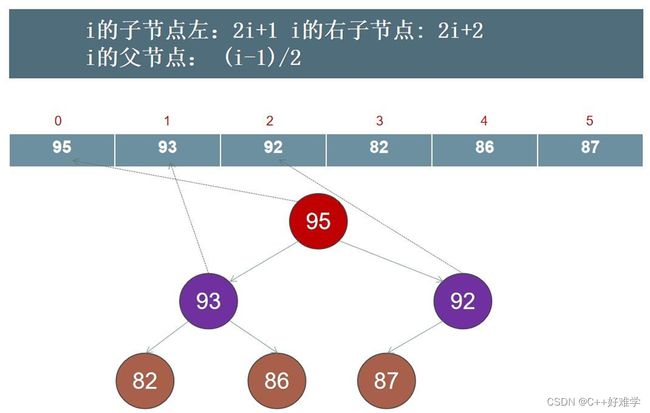
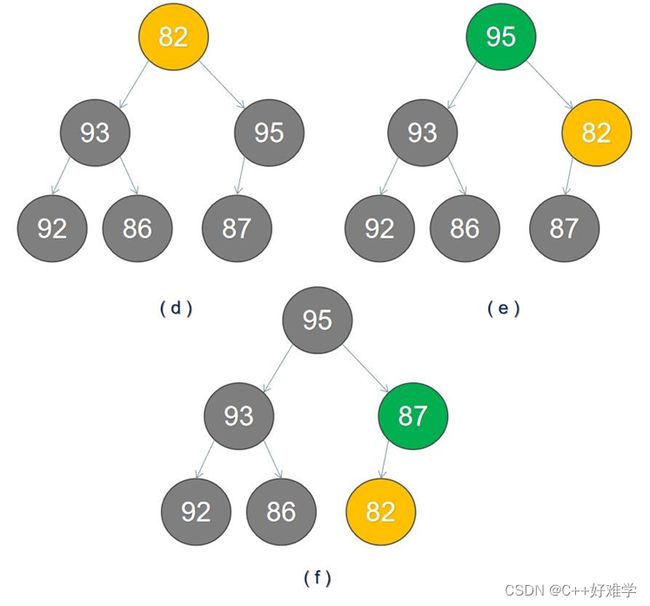
首先我们需要找到最后一个结点的父结点如图(a),我们找到的结点是 87-----------利用:( i - 1 ) / 2
-
然后找出该结点的最大子节点与自 己比较,若该子节点比自身大,则将两个结点交换.
-
图(a)中,87 比左子节点 95 小,则交换之.如图(b)所示
第二步:
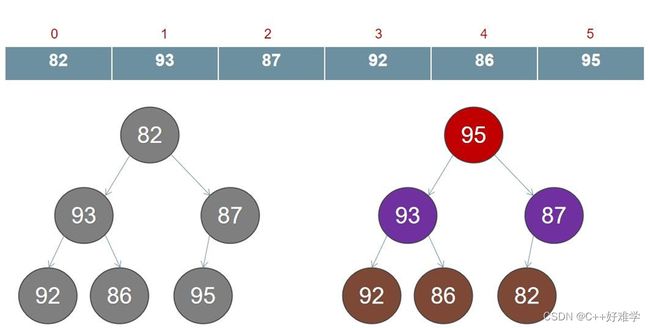
- 我们移动到前一个父结点 93,如图©所示.同理做第一步的比较操作,结果不需要交换
第三步:
- 继续移动结点到前一个父结点 82,如图(d)所示,82 小于右子节点 95,则 82 与 95 交换,
- 如图(e)所示,82 交换后,其值小于左子节点,不符合最大堆的特点,故需要继续向下调整,如图(f)所示
所有节点交换完毕,最大堆构建完成
最大堆的代码实现
程序为了使函数更通用,向上调整设为循环,使后面的插入元素可以直接调用API
#include
#include
using namespace std;
#define MAX 128
//最大堆
struct MyHeap
{
int *arr;
int size;
int capacity;
};
//static+函数/变量表示:文件内部的函数/变量,外部文件不可以访问
//通常只把需要用到的接口提供给别人
//向下调整
static void adjustDown(MyHeap & myHeap, int index)
{
int father, son;
//father * 2 + 1 < myHeap.size; 只要保证左节点不超过最大节点数就可以,这里不需要考虑右节点数
//father = son;第一轮循环不会执行,但是之后的都会执行
for (int father = index; father * 2 + 1 < myHeap.size; father = son)
{
son = father * 2 + 1;
//找出两个子节点最大数,
//son + 1 < myHeap.size:若为false,则没有右节点
if ((son + 1 < myHeap.size) && (myHeap.arr[son] < myHeap.arr[son + 1]))
{
son++;
}
if (myHeap.arr[son] > myHeap.arr[father])
{
int temp = myHeap.arr[father];
myHeap.arr[father] = myHeap.arr[son];
myHeap.arr[son] = temp;
}
else
{
break;
}
}
}
//用于找出父类的下标
static void creatHeap(MyHeap & myHeap)
{
for (int i = (myHeap.size - 1 - 1) / 2; i >= 0; i--)
{
adjustDown(myHeap, i);
}
}
//初始化最大堆
bool initHeap(MyHeap & myHeap, int capacity, int * arr)
{
if (arr == NULL || capacity < 0)
{
cout << "传入参数无效" << endl;
return false;
}
myHeap.size = capacity;
myHeap.capacity = MAX > capacity ? MAX : capacity;
myHeap.arr = new int[myHeap.capacity];
memcpy(myHeap.arr, arr, sizeof(int)*capacity);
if (myHeap.arr == NULL)
{
cout << "内存申请失败" << endl;
return false;
}
creatHeap(myHeap);
return true;
}
int main()
{
MyHeap heap;
int arr[] = { 82,93,87,92,86,95 };
initHeap(heap, sizeof(arr) / sizeof(arr[0]), arr);
for (int i = 0; i < 6; i++)
{
cout << heap.arr[i] << endl;
}
system("pause");
return 0;
}
插入新元素and堆顶元素出列
插入新元素
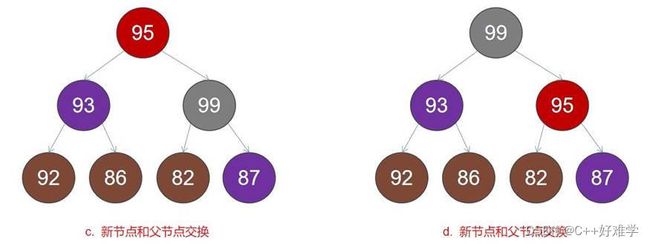
- 将数字 99 插入到上面大顶堆中的过程如下:
1) 原始的堆,如图 a
- 对应的数组:{95, 93, 87, 92, 86, 82}
2) 将新进的元素插入到大顶堆的尾部,如下图 b 所示:
-
b. 加入新的元素
-
对应的数组:{95, 93, 87, 92, 86, 82, 99}
3) 此时最大堆已经被破坏,需要重新调整, 因加入的节点比父节点大,则新节点跟父节点调换即可,如图 c 所示;调整后,新节点如果比新的父节点小,则已经调整到位,如果比新的父节点大,则需要和父节点重新进行交换,如图 d, 至此,最大堆调整完成。
实现所用API
//插入元素
void insertData(MyHeap & myHeap, int data)
{
if (isFull(myHeap))
{
cout << "不好意思容器已满" << endl;
return;
}
myHeap.arr[myHeap.size] = data;
myHeap.size++;
//向下调整
adjustUp(myHeap, myHeap.size - 1);
}
//向下调整
void adjustUp(MyHeap & myHeap, int index)
{
if (index < 0)
{
cout << "传入参数无效" << endl;
return;
}
int father, son;
for (int son = index; (son - 1) / 2 >= 0; son = father)
{
father = (son - 1) / 2;
if (myHeap.arr[son] > myHeap.arr[father])
{
int temp = myHeap.arr[son];
myHeap.arr[son] = myHeap.arr[father];
myHeap.arr[father] = temp;
}
else
{
break;
}
}
}
//判断是否已经满了
bool isFull(MyHeap & myHeap)
{
if (myHeap.size == myHeap.capacity)
{
return true;
}
return false;
}
堆顶元素出列
-
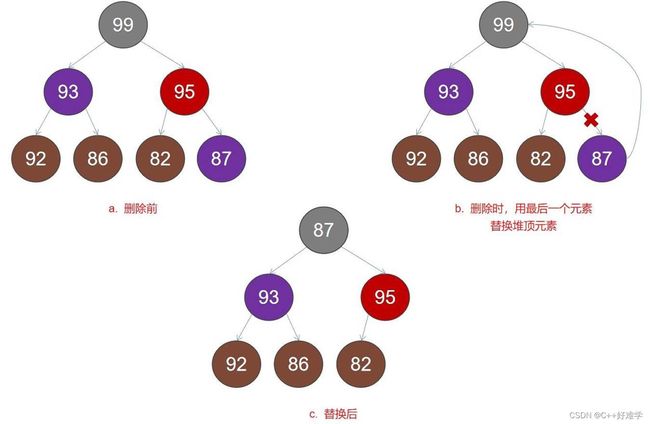
如果我们将堆顶的元素删除,那么顶部有一个空的节点,怎么处理?
-
当插入节点的时候,我们将新的值插入数组的尾部。现在我们来做相反的事情:我们取出数组中的最后一个元素,将它放到堆的顶部,然后再修复堆属性。
实现所用API
//删除头部元素
void popHeadData(MyHeap & myHeap)
{
if (isEmpty(myHeap))
{
cout << "不好意思容器为空" << endl;
return;
}
if (myHeap.size == 1)
{
myHeap.size--;
return;
}
myHeap.arr[0] = myHeap.arr[myHeap.size - 1];
myHeap.size--;
//向下调整
adjustDown(myHeap, 0);
}
//向下调整,堆创建的时候也用这个API
void adjustDown(MyHeap & myHeap, int index)
{
if (index < 0)
{
cout << "传入参数无效" << endl;
}
int father, son;
for (int father = index; father * 2 + 1 < myHeap.size; father = son)
{
son = father * 2 + 1;
if ((son + 1 < myHeap.size) && (myHeap.arr[son + 1] > myHeap.arr[son]))
{
son++;
}
if (myHeap.arr[son] > myHeap.arr[father])
{
int temp = myHeap.arr[son];
myHeap.arr[son] = myHeap.arr[father];
myHeap.arr[father] = temp;
}
else
{
break;
}
}
}
//判断是否为空
bool isEmpty(MyHeap & myHeap)
{
if (myHeap.size == 0)
{
return true;
}
return false;
}
优先队列
- 操作系统内核作业调度是优先队列的一个应用实例,它根据优先级的高低而不是先到先服务的方式来进行调度;
如果最小键值元素拥有最高的优先级,那么这种优先队列叫作升序优先队列(即总是先删除最小
的元素),类似的,如果最大键值元素拥有最高的优先级,那么这种优先队列叫作降序优先队列
(即总是先删除最大的元素);由于这两种类型是完全对称的,所以只需要关注其中一种,如升
序优先队列.
MyHeap.h
#pragma once
#include
using namespace std;
#include
#define MAX 128
template
struct MyHeap
{
int size;
int capacity;
T * arr;
};
//初始化
template
void initMyHeap(MyHeap & myHeap , int size , vector & v);
//插入元素
template
void insertData(MyHeap & myHeap, T & data);
//移除头部元素
template
void popHeadData(MyHeap & myHeap);
//堆排序
template
int sortMyHeap(MyHeap & myHeap);
//销毁堆
template
void desroryHead(MyHeap & myHeap);
//创建堆
template
static void creatHeap(MyHeap & myHeap);
//向下调整
template
static void adjustDown(MyHeap & myHeap, int index);
//向上调整
template
static void adjustUp(MyHeap & myHeap, int index);
//判断堆是否已经满了
template
static bool isFull(MyHeap & myHeap);
//判断堆是否为空
template
static bool isEmpty(MyHeap & myHeap);
MyHeap.cpp
#include "MyHeap.h"
template
void initMyHeap(MyHeap & myHeap , int size , vector & v)
{
if (v.size() == 0)
{
cout << "不好意思传入参数无效" << endl;
}
myHeap.size = size;
myHeap.capacity = MAX > size ? MAX : size;
myHeap.arr = new T[myHeap.capacity];
for (int i = 0; i < size; i++)
{
myHeap.arr[i] = v[i];
}
creatHeap(myHeap);
}
template
void insertData(MyHeap & myHeap, T & data)
{
if (isFull(myHeap))
{
cout << "不好意思容器已满" << endl;
return;
}
myHeap.arr[myHeap.size] = data;
myHeap.size++;
//向下调整
adjustUp(myHeap, myHeap.size - 1);
}
template
void popHeadData(MyHeap & myHeap)
{
if (isEmpty(myHeap))
{
cout << "不好意思容器为空" << endl;
return;
}
if (myHeap.size == 1)
{
myHeap.size--;
return;
}
T temp = myHeap.arr[0];
myHeap.arr[0] = myHeap.arr[myHeap.size - 1];
myHeap.arr[myHeap.size - 1] = temp;
myHeap.size--;
//向下调整
adjustDown(myHeap, 0);
}
//堆排序
template
int sortMyHeap(MyHeap& myHeap)
{
//在移除元素的过程中size会发生改变
int temp = myHeap.size;
int size = myHeap.size;
for (int i = 0; i < temp; i++)
{
popHeadData(myHeap);
}
return size;
}
template
void desroryHead(MyHeap& myHeap)
{
if (myHeap.arr != NULL)
{
delete[] myHeap.arr;
}
myHeap.capacity = myHeap.size = 0;
}
template
void creatHeap(MyHeap & myHeap)
{
//其中(myHeap.size-1-1)/2 代表下标最大的父类
for (int i = (myHeap.size - 1 - 1) / 2; i >= 0; i--)
{
adjustDown(myHeap, i);
}
}
template
void adjustDown(MyHeap & myHeap, int index)
{
if (index < 0)
{
cout << "传入参数无效" << endl;
}
int father, son;
for (int father = index; father * 2 + 1 < myHeap.size; father = son)
{
son = father * 2 + 1;
if ((son + 1 < myHeap.size) && (*myHeap.arr[son + 1] > *myHeap.arr[son]))
{
son++;
}
if (*myHeap.arr[son] > *myHeap.arr[father])
{
T temp = myHeap.arr[son];
myHeap.arr[son] = myHeap.arr[father];
myHeap.arr[father] = temp;
}
else
{
break;
}
}
}
template
void adjustUp(MyHeap & myHeap, int index)
{
if (index < 0)
{
cout << "传入参数无效" << endl;
return;
}
int father, son;
for (int son = index; (son - 1) / 2 >= 0; son = father)
{
father = (son - 1) / 2;
if (*myHeap.arr[son] > *myHeap.arr[father])
{
int temp = myHeap.arr[son];
myHeap.arr[son] = myHeap.arr[father];
myHeap.arr[father] = temp;
}
else
{
break;
}
}
}
template
bool isFull(MyHeap & myHeap)
{
if (myHeap.size == myHeap.capacity)
{
return true;
}
return false;
}
template
bool isEmpty(MyHeap & myHeap)
{
if (myHeap.size == 0)
{
return true;
}
return false;
}
main.cpp
注意:添加模板文件的时候要添加.cpp文件
#include
#include
#include
#include"MyHeap.cpp"
using namespace std;
//大于 小于 等于
class Person
{
public:
Person(){}
Person(int age, string name)
{
this->age = age;
this->name = name;
}
int age;
string name;
};
bool operator>(Person & P1, Person & P2)
{
return P1.age > P2.age;
}
bool operator<(Person & P1, Person & P2)
{
return P1.age < P2.age;
}
ostream & operator<<(ostream & out, Person P)
{
out << P.age << " " << P.name ;
return out;
}
int main()
{
//传入指针减少资源损耗
Person P1 = Person(82, "小李");
Person P2 = Person(93, "小崔");
Person P3 = Person(87, "小王");
Person P4 = Person(92, "小帅");
Person P5 = Person(86, "小钟");
Person P6 = Person(95, "小江");
vector v;
v.push_back(&P1);
v.push_back(&P2);
v.push_back(&P3);
v.push_back(&P4);
v.push_back(&P5);
v.push_back(&P6);
MyHeap myHeap;
//输出最大堆
initMyHeap (myHeap, v.size(), v);
for (int i = 0; i < myHeap.size; i++)
{
cout << *myHeap.arr[i] << endl;
}
cout << "-------------------------------------" << endl;
//把成绩按从小到大输出
int size = sortMyHeap(myHeap);
for (int i = 0; i < size; i++)
{
cout << *myHeap.arr[i] << endl;
}
cout << "-------------------------------------" << endl;
//输出前三名
int num = 3;
while (num--)
{
if (size < 0)
{
break;
}
cout << *myHeap.arr[size-1] << endl;
size--;
}
system("pause");
return 0;
}
堆排序
- 堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法,它是选择排序的一种。可以利用数组的特
点快速定位指定索引的元素.
(选择排序工作原理 - 第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,
然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾。以此类推,直到全部待
排序的数据元素的个数为零)
- 相比于上面代码添加一个API即可实现从小到大的排序
//堆排序
template
int sortMyHeap(MyHeap& myHeap)
{
//在移除元素的过程中size会发生改变
int temp = myHeap.size;
int size = myHeap.size;
for (int i = 0; i < temp; i++)
{
popHeadData(myHeap);
}
return size;
}