【STL】容器 - set和map的使用与实现
目录
前言
一.键值对
1.在SGI - STL中对键值对的定义:
2.make_pair
3. pair支持直接比较大小
二.set
1.set的概念与注意事项
2.set的使用(常用接口)
<1>.构造函数
<2>.迭代器与范围for
<3>.插入和查找
<4>.删除erase
<5>.计数count
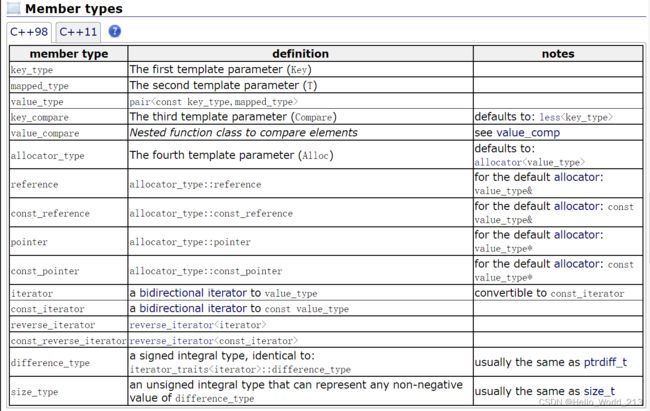
三.map
1.map的概念与注意事项
2.map的使用(常用接口)
<1>.构造函数
<2>.迭代器与范围for
<3>.查找find
<4>插入insert
<5>.删除erase
<6>.计数count
<7>.operator[]与at(重点)
四.set/map模拟实现
1.前言
2.RBTree实现
3.set实现
4.map实现
前言
序列式容器与关联式容器
序列式容器:
string, vector, list, deque是序列式容器, 其底层都为线性结构, 在结构上没有其余特点, 里面存储的值是元素本身
关联式容器:
set, map, multiset, multimap是关联式容器, 其底层的结构有一定的特性与规则, 存储的是
set和map, multiset和multimap
set和map的底层都是用红黑树实现的, 都自带去重
set和map的区别: set存储key, map存储key/value
multiset, multimap和set, map的区别: multiset, multimap不会去重, 其余都相同
由于其他内容过于相似, 只是去不去重的问题, 本篇博客主要介绍set和map, 对于multiset和multimap的介绍更像是基于map和set的扩展
一.键值对
一对用来表示一对对应关系, 经典的
在stl中, 用pair类将键值对进行了封装, 一个pair类对象就是一个键值对
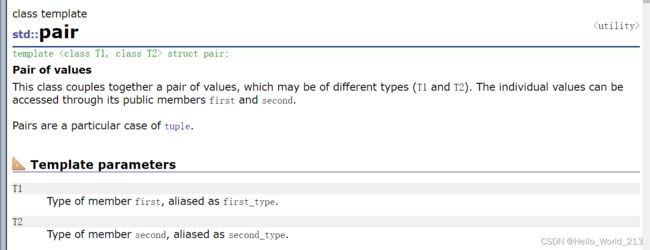
1.在SGI - STL中对键值对的定义:
template
struct pair
{
typedef T1 first_type;
typedef T2 second_type;
//默认构造
pair()
:first(T1())
, second(T2())
{}
//有参构造
pair(const T1& a, const T2& b)
:first(a)
, second(b)
{}
//成员变量
T1 first; // key
T2 second;// value
}; 2.make_pair
make_pair是C++提供的一个函数模板, 用来构建pair对象
为了使用者在创建键值对对象时更加轻松, 不用再去写过长的模板参数, 而是可以通过函数模板自动类型推导(这一点在使用map时会深有体会)
//模拟实现
template
pair& make_pair(const T1& first, const T2& second)
{
return pair(first, second);
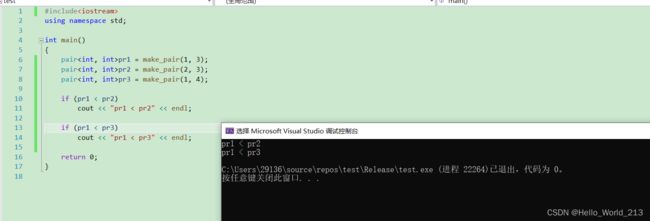
} 3. pair支持直接比较大小
pair
比较规则: 先比first, 如果first相等, 就去比second
二.set
1.set的概念与注意事项
1.set中只可以存储key, 从更严谨的角度: set也可以存储键值对, 但是是将整个键值对当作key来存储的
2.set支持增删查, 而并不支持修改操作, 因为key是不可以被修改的
3.set的底层使用红黑树实现
4.set的查找效率是OlogN
5.set中不可以存储相同数据, 故可以达到去重的效果
6.set可以自己控制仿函数, 可以按照自己的比较规则来实现, 默认情况下使用less仿函数, 中序遍历是一个升序序列, 相反如果使用greater仿函数, 中序遍历就是一个降序序列
2.set的使用(常用接口)
set中元素不是连续存储的, 每个元素也只是一个单一的值, 所以不支持operator[]
<1>.构造函数
//构造函数
void set_test1()
{
//默认构造
set s1;
//迭代器区间构造
vector v = { 7,2,4,3,5,1,9 };
set s2(v.begin(), v.end());
//拷贝构造
set s3(s2);//or: set s3 = s2;
//C++11新增构造函数
set s = { 7,2,4,3,5,1,9 };
} <2>.迭代器与范围for
void set_test2()
{
//正向遍历:
//默认使用less仿函数
set s = { 7,2,4,3,5,1,9 };
//正向迭代器 - 底层是中序遍历
set::iterator it = s.begin();
while (it != s.end())
{
cout << *it++ << ' ';
}
cout << endl;
//范围for
for (auto& elem : s)
{
cout << elem << ' ';
}
cout << endl;
//反向遍历:
//方法一: 反向迭代器 reverse_iterator, rbegin(), rend()
set::reverse_iterator rit = s.rbegin();
while (rit != s.rend())
{
cout << *rit++ << ' ';
}
cout << endl;
//方法二:
//显式使用greater仿函数, 改变值的比较规则, 需要包头文件functional
set> s2 = { 7,2,4,3,5,1,9 };
set::iterator it2 = s2.begin();
while (it2 != s2.end())
{
cout << *it2++ << ' ';
}
cout << endl;
//范围for
for (auto& elem : s2)
{
cout << elem << ' ';
}
cout << endl;
} <3>.插入和查找
void set_test4()
{
set s = { 7,2,4 };
s.insert(3);
s.insert(5);
s.insert(1);
s.insert(9);
for (auto& elem : s)
{
cout << elem << ' ';
}
cout << endl;
set::iterator pos = s.find(5);
if (pos != s.end())
{
cout << *pos << " is find" << endl;
}
} 在multiset中查找会找到中序遍历中的第一个符合条件的值
multiset ms = { 5,6,8,12,1,5,3,12,9,4,2,5 };
for (auto& elem : ms)
{
cout << elem << ' ';
}
cout << endl;
multiset::iterator pos = ms.find(5);
while (pos != ms.end())
{
cout << *pos << ' ';
pos++;
}
cout << endl; multiset的插入会插入到所有相同值的最右侧, 也就是中序遍历的最后一个
且set的insert与multiset的insert返回值类型不同
multiset ms = { 5,6,8,12,1,5,3,12,9,4,2,5 };
for (auto& elem : ms)
{
cout << elem << ' ';
}
cout << endl;
multiset::iterator pos = ms.insert(5);;
while (pos != ms.end())
{
cout << *pos << ' ';
pos++;
}
cout << endl;
for (auto& elem : ms)
{
cout << elem << ' ';
} <4>.删除erase
void set_test3()
{
set s = { 7,2,4,3,5,1,9 };
//set容器的erase接口既可以传值删除, 又可以传iterator删除
//有什么区别?
s.erase(3);
for (auto& elem : s)
{
cout << elem << ' ';
}
cout << endl;
set::iterator pos = s.find(4);
if (pos != s.end())
{
s.erase(pos);
}
for (auto& elem : s)
{
cout << elem << ' ';
}
cout << endl;
}
set容器的erase接口既可以传值删除, 又可以传iterator删除, 有什么区别?
如果传入的是iterator, 则必须要走一步find操作, 在底层看来erase的传值删除实际是封装了先调用find查找, 再使用find返回的iterator删除这两步
上面是删除存在的数据, 如果此时删除一个不存在的数据且不用if(pos != s.end())进行判断, 传iterator删除是有问题的, 因为如果find找不到对应数据会返回end(), 所以erase传值删除的底层也是封装了find, 如果返回end(), erase底层会有检查, 所以如果是传iterator删除, 需要手动添加if(pos != s.end())这个条件, 否则如果数据不存在就会有问题
在multiset中会存在重复元素, erase会删除所有存在的元素
void multiset_test()
{
multiset ms = { 5 ,6,8,12,1,5,3,12,9,4,2,5 };
for (auto& elem : ms)
{
cout << elem << ' ';
}
cout << endl;
ms.erase(5);
for (auto& elem : ms)
{
cout << elem << ' ';
}
cout << endl;
} <5>.计数count
set为了与multiset保持一致也支持了这个接口, 因为set中不能存放重复数据所以count只有1或这是0
但在multiset中, count可以统计这个元素存在多少个
multiset ms = { 5,6,8,12,1,5,3,5,9,4,2,5 };
for (auto& elem : ms)
{
cout << elem << ' ';
}
cout << endl;
cout << "数字5有: " << ms.count(5) << "个" << endl; 三.map
1.map的概念与注意事项
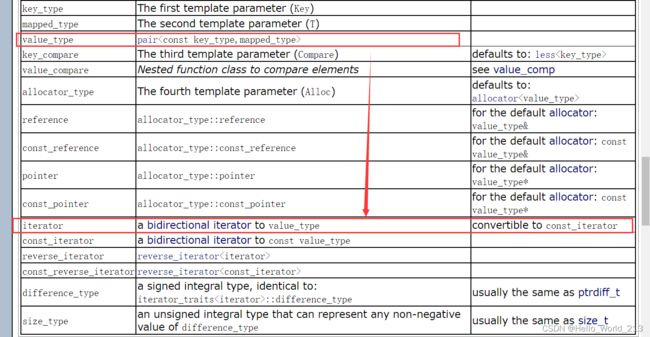
1.map中存储的是键值对 --- pair
2.map支持增删查改, 这个改指的是value可以修改, key不可以修改
3.map的底层使用红黑树实现
4.map的查找效率是OlogN
5.map中不可以存储相同数据, 故可以达到去重的效果
6.map可以自己控制仿函数, 可以按照自己的比较规则来实现, 默认情况下使用less仿函数, 中序遍历是一个升序序列, 相反如果使用greater仿函数, 中序遍历就是一个降序序列
7.map中存储的是键值对pair
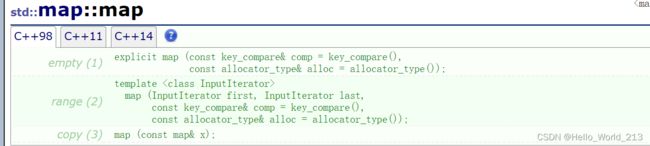
2.map的使用(常用接口)
<1>.构造函数
void map_test1()
{
//默认构造
map m1;
//迭代器区间构造
pair kv1("home", "家");
pair kv2("happy", "高兴");
pair kv3("sort", "排序");
vector> v = { kv1,kv2,kv3 };
map m2(v.begin(), v.end());
//拷贝构造
map m3(m2);
} <2>.迭代器与范围for
void map_test2()
{
pair kv1("home", "家");
pair kv2("happy", "高兴");
pair kv3("sort", "排序");
vector> v = { kv1,kv2,kv3 };
map m(v.begin(), v.end());
//迭代器遍历
map::iterator it = m.begin();
while (it != m.end())
{
cout << it->first << "-" << it->second << ' ';
it++;
}
cout << endl;
//范围for遍历
for (auto& elem : m)
{
cout << elem.first << "-" << elem.second << ' ';
}
cout << endl;
} <3>.查找find
void map_test3()
{
pair kv1("home", "家");
pair kv2("happy", "高兴");
pair kv3("sort", "排序");
vector> v = { kv1,kv2,kv3 };
map m(v.begin(), v.end());
//根据键值查找
map::iterator pos = m.find("happy");
//如果没找到, m.find()返回m.end()
if (pos != m.end())
{
cout << pos->first << '-' << pos->second << endl;
}
} <4>插入insert
这里insert的返回值是pair
void map_test4()
{
map m;
//第一种插入方式, 先构造对象, 再插入
pair kv("good", "好");
m.insert(kv);
//第二种插入方式, 匿名对象
m.insert(pair("bad", "坏"));
//第三种插入方式, 使用make_pair函数模板
m.insert(make_pair("beautiful", "漂亮"));
for (auto& elem : m)
{
cout << elem.first << "-" << elem.second << ' ';
}
cout << endl;
} <5>.删除erase
void map_test5()
{
pair kv1("home", "家");
pair kv2("happy", "高兴");
pair kv3("sort", "排序");
vector> v = { kv1,kv2,kv3 };
map m(v.begin(), v.end());
for (auto& elem : m)
{
cout << elem.first << "-" << elem.second << ' ';
}
cout << endl;
//传迭代器删除
map::iterator pos = m.find("happy");
if (pos != m.end())
{
m.erase(pos);
}
for (auto& elem : m)
{
cout << elem.first << "-" << elem.second << ' ';
}
cout << endl;
//传key值删除
cout << m.erase("home") << endl;
for (auto& elem : m)
{
cout << elem.first << "-" << elem.second << ' ';
}
cout << endl;
} <6>.计数count
与set一样, count函数也是为multimap准备的, map中的count只是为了与multimap保持一致
<7>.operator[]与at(重点)
首先强调:
set, multiset是没有重载operator[]的, 原因很简单, set系列是key模型, 并不存在value
multimap也不支持operator[], 这是因为在multimap中允许插入重复的key值, 这样就违背了operator[]的意图, 所以自然也就没有支持operator[]
在map中重载的operator[]是根据key返回对应的value的引用
map中的operator[]存在两种情况
1.传入的key值存在在map中, 则operator[]执行: 查找+修改value
2.传入的key值不存在于map中, 则operator[]执行: 插入+修改value
如果这里insert没有返回这个pair
解释insert的返回值pair
由于map不会插入重复的键值, 插入时如果该键值已经存在, 则直接返回存在的这个键值对的迭代器, 如果插入的键值不存在, 则先插入, 后返回插入的这个键值对的迭代器, 但是需要插入的是
注: 对于内置类型, 例如int而言, int()这难道也要去调用int的默认构造吗? C++为了兼容自定义类型, 规定如int()这样的值就默认为0, float()就是0.0
这样operator[]的实现就可以复用一个insert就可以了
void map_test6()
{
string str_array[] = { "老师", "学生", "校长","学生" ,"学生" ,"学生" ,"学生" ,"学生" ,"学生","老师","老师" };
//统计老师,学生,校长各自的人数
map m;
for (int i = 0; i < sizeof(str_array) / sizeof(str_array[0]); ++i)
{
m[str_array[i]]++;
}
for (auto& elem : m)
{
cout << elem.first << "-" << elem.second << ' ';
}
cout << endl;
} 对operator[]实现的解读
(this->insert(make_pair(key, value))) --- 拿到insert返回值 --- pair
( (this->insert(make_pair(key, value))) ).first --- 根据拿到的返回值对象, 去访问第一个成员iterator, 这个iterator是新插入或者查找到的key的键值对
(* ( (this->insert(make_pair(key, value))) ).first ).second --- 对拿到的iterator解引用, 在去访问iterator的第二个成员value, 以引用的形式返回
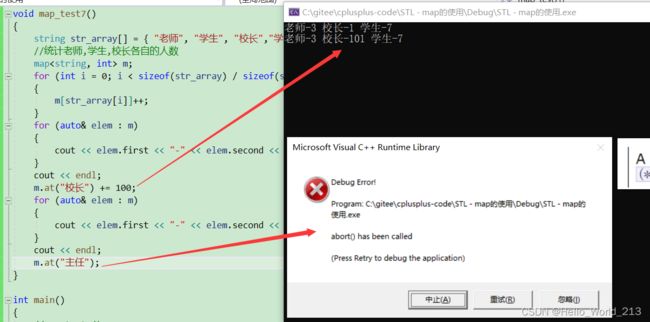
对于at而言, 只有查找+修改value的功能, 如果找不到就会抛出异常
void map_test7()
{
string str_array[] = { "老师", "学生", "校长","学生" ,"学生" ,"学生" ,"学生" ,"学生" ,"学生","老师","老师" };
//统计老师,学生,校长各自的人数
map m;
for (int i = 0; i < sizeof(str_array) / sizeof(str_array[0]); ++i)
{
m[str_array[i]]++;
}
for (auto& elem : m)
{
cout << elem.first << "-" << elem.second << ' ';
}
cout << endl;
m.at("校长") += 100;
for (auto& elem : m)
{
cout << elem.first << "-" << elem.second << ' ';
}
cout << endl;
m.at("主任");
} 四.set/map模拟实现
1.前言
map和set容器的底层使用的红黑树, set只存储值, map存储键值对
为了体现复用思想, 红黑树存储类型统一为K/T模型, 如果是set实现T则传K, map实现T则传pair
再通过仿函数KeyOfT来取到T中的K类型对象key
注: 以下只是模拟实现的迭代器/插入功能
2.RBTree实现
#define _CRT_SECURE_NO_WARNINGS 1
#pragma once
enum Color
{
RED,
BLACK
};
template
struct RBTreeNode
{
RBTreeNode* _left;
RBTreeNode* _right;
RBTreeNode* _parent;
Color _col;
T _val;
//构造
RBTreeNode(const T& val)
:_left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _col(RED)//默认添加的新节点为红色
, _val(val)
{}
};
template
struct Iterator
{
typedef RBTreeNode Node;
typedef Iterator Self;
Iterator(Node* node)
:_node(node)
{}
Ref operator*()
{
return _node->_val;
}
Ptr operator->()
{
//return &(_node->_val);
return &(*Iterator(_node));
}
bool operator==(const Self& val)const
{
return _node == val._node;
}
bool operator!=(const Self& val)const
{
return _node != val._node;
}
//前置++
Self& operator++()
{
if (_node->_right != nullptr)
{
//找右节点为根节点的最左节点
Node* left = _node->_right;
while (left->_left != nullptr)
{
left = left->_left;
}
_node = left;
}
else
{
Node* parent = _node->_parent;
Node* cur = _node;
//如果当前是父的左,说明还没走过,下一步要走到父;
//如果当前是父的右,说明已经走过了,下一步循环判断父是爷的左还是右,重复这个过程
while (parent && parent->_right == cur)
{
cur = parent;
parent = parent->_parent;
}
//出循环说明1.parent为nullptr说明到了end()2.当前是父的左
//结论:下一步都要走到parent
_node = parent;
}
return *this;
}
//前置--
//与前置++逻辑逆置
Self& operator--()
{
if (_node->_left != nullptr)
{
Node* right = _node->_left;
while (right->_right != nullptr)
{
right = right->_right;
}
_node = right;
}
else
{
Node* parent = _node->_parent;
Node* cur = _node;
while (parent && cur == parent->_left)
{
cur = parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
Node* _node;
};
template
class RBTree
{
public:
typedef RBTreeNode Node;
typedef Iterator iterator;
iterator begin()
{
Node* cur = root;
while (cur && cur->_left != nullptr)
{
cur = cur->_left;
}
return iterator(cur);
}
iterator end()
{
return iterator(nullptr);
}
pair insert(const T& val)
{
KeyOfT key;
if (root == nullptr)
{
//如果此时为空树
root = new Node(val);
//将根节点修正为黑色
root->_col = BLACK;
return make_pair(iterator(root), true);
}
Node* cur = root;
Node* parent = nullptr;//cur的父节点
while (cur)
{
if (key(cur->_val) > key(val))
{
parent = cur;
cur = cur->_left;
}
else if (key(cur->_val) < key(val))
{
parent = cur;
cur = cur->_right;
}
else
{
//如果插入的节点是重复值, 则插入失败
return make_pair(iterator(cur), false);
}
}
cur = new Node(val);
if (key(parent->_val) > key(cur->_val))
{
parent->_left = cur;
}
else if (key(parent->_val) < key(cur->_val))
{
parent->_right = cur;
}
cur->_parent = parent;
//以上为插入节点
//-------------------------------------------------------
//以下为调整为红黑树
//因为默认插入的节点为红色,所以如果出现了两个连续为红的节点就需要处理
while (parent && parent->_col == RED)
{
Node* grandfather = parent->_parent;
Node* uncle = nullptr;
//确定叔叔节点的位置
if (grandfather->_left == parent)
{
uncle = grandfather->_right;
}
else//grandfather->_right == parent
{
uncle = grandfather->_left;
}
//将分为三种情况
//1.父节点为红,叔叔节点存在且为红(变色 + 向上迭代)
//2/3.父节点为红,叔叔节点不存在或者存在且为黑(旋转 + 变色)
if (uncle && uncle->_col == RED)//情况一
{
//父变黑,叔叔变黑,祖父变红->向上迭代
parent->_col = BLACK;
uncle->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = cur->_parent;
}
else//情况二/三
{
//情况二
// g
// p u
// c
if (uncle == grandfather->_right && cur == parent->_left)
{
//右单旋
RotateR(grandfather);
//
parent->_col = BLACK;
grandfather->_col = RED;
break;
}
// g
// u p
// c
else if (uncle == grandfather->_left && cur == parent->_right)
{
//左单旋
RotateL(grandfather);
//
parent->_col = BLACK;
grandfather->_col = RED;
break;
}
//情况三
// g
// u p
// c
else if (uncle == grandfather->_left && cur == parent->_left)
{
//左双旋
RotateRL(grandfather);
//
grandfather->_col = RED;
cur->_col = BLACK;
break;
}
// g
// p u
// c
else if (uncle == grandfather->_right && cur == parent->_right)
{
//右双旋
RotateLR(grandfather);
//
grandfather->_col = RED;
cur->_col = BLACK;
break;
}
else
{
cout << "不存在这种情况" << endl;
exit(-1);
}
}
}
root->_col = BLACK;
return make_pair(iterator(cur), true);
}
void inorder()
{
_inorder(root);
}
bool isRBTree()
{
if (root->_col == RED)
{
cout << "出错: 根节点为红" << endl;
return false;
}
//判断是否有连续红节点,且每条路径的黑节点是否相等
int benchmark = 0;//算出最左路径的黑节点个数
Node* cur = root;
while (cur)
{
if (cur->_col == BLACK)
{
++benchmark;
}
cur = cur->_left;
}
return _isRBTree(root, 0, benchmark);
}
private:
//四种旋转
void RotateL(Node* prev)
{
Node* subR = prev->_right;
Node* subRL = subR->_left;
Node* ppNode = prev->_parent;
prev->_right = subRL;
if (subRL)
{
subRL->_parent = prev;
}
subR->_left = prev;
prev->_parent = subR;
if (root == prev)
{
root = subR;
}
else
{
if (ppNode->_left == prev)
{
ppNode->_left = subR;
}
else
{
ppNode->_right = subR;
}
}
subR->_parent = ppNode;
}
void RotateR(Node* prev)
{
Node* subL = prev->_left;
Node* subLR = subL->_right;
Node* ppNode = prev->_parent;
subL->_right = prev;
prev->_parent = subL;
prev->_left = subLR;
if (subLR)
{
subLR->_parent = prev;
}
if (root == prev)
{
root = subL;
}
else
{
if (ppNode->_left == prev)
{
ppNode->_left = subL;
}
else
{
ppNode->_right = subL;
}
}
subL->_parent = ppNode;
}
void RotateRL(Node* prev)
{
//先右旋, 再左旋
RotateR(prev->_right);
RotateL(prev);
}
void RotateLR(Node* prev)
{
//先左旋, 再右旋
RotateL(prev->_left);
RotateR(prev);
}
void _inorder(Node* root)
{
if (root)
{
_inorder(root->_left);
cout << root->_kv.first << "--" << root->_kv.second << endl;
_inorder(root->_right);
}
}
bool _isRBTree(Node* root, int blackNum, int benchmark)
{
if (root == nullptr)//走到空节点
{
if (benchmark == blackNum)
{
//for debug
//cout << blackNum << endl;
return true;
}
else
{
//for debug
//cout << blackNum << endl;
cout << "不是所有路径的黑色节点个数都相同" << endl;
return false;
}
}
if (root->_col == BLACK)
{
++blackNum;
}
//判断是否有连续的红节点
if (root->_col == RED && root->_parent->_col == RED)
{
cout << "出现了连续的红色节点" << endl;
return false;
}
return _isRBTree(root->_left, blackNum, benchmark)
&& _isRBTree(root->_right, blackNum, benchmark);
}
Node* root = nullptr;
}; 3.set实现
#define _CRT_SECURE_NO_WARNINGS 1
#include"RBTree.h"
template
class Set
{
public:
struct SetKeyOfT
{
const K& operator()(const K& key)
{
return key;
}
};
typedef typename RBTree::iterator iterator;
pair insert(const K& key)
{
return _t.insert(key);
}
iterator begin()
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
private:
RBTree _t;
}; 4.map实现
#define _CRT_SECURE_NO_WARNINGS 1
#include"RBTree.h"
template
class Map
{
public:
struct MapKeyOfT
{
const K& operator()(const pair& kv)
{
return kv.first;
}
};
typedef typename RBTree, MapKeyOfT>::iterator iterator;
pair insert(const pair& kv)
{
return _t.insert(kv);
}
V& operator[](const K& key)
{
pair ret = insert(make_pair(key, V()));
return ret.first->second;
}
iterator begin()
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
private:
RBTree, MapKeyOfT> _t;
};