常用算法——查找算法

    查找：在一些数据元素中，通过一定的方法找出与给定关键字相同数据的元素的过程称为查找。实现查找的方法称查找算法。

    查找算法大致可分为七大查找算法：

• 顺序查找
• 二分查找
• 插值查找
• Fibonacci查找
• 分块查找
• 树表查找
• HashTable查找

    本篇介绍其中的前四种查找算法。

一、顺序查找(线性查找)

    顺序查找也称为线性查找，顺序查找属于原始、穷举、暴力查找算法。容易理解、编码实现也简单。但是在数据量较多时，因其算法思想是朴素、穷举的，算法中没有太多优化设计，性能会很低下。

顺序查找思想：

1、按照序列原有顺序对数组或列表进行遍历比较查询的基本查找算法。

2、对于任意一个序列以及一个给定的元素，将给定元素与序列中元素依次比较，直到找出与给定关键字相同的元素，或者将序列中的元素与其都比较完为止。

时间复杂度：

问题规模：列表的长度(n)

O(1)：当查找的元素位于列表第一位时，最好的情况

O(n)：遍历列表所有元素，最坏的情况

顺序查找算法完整程序(函数)如下：

def linear_search(li, val):
    for ind, v in enumerate(li): # 枚举列表的索引和值
        if v == val:
            return ind, li[ind]
        else:
            return None

二、二分查找(折半查找)

    二分查找也称折半查找(Binary Search)，它是一种效率较高的查找方法。二分查找属于有序查找，所谓有序查找，指被查找的数列必须是有序的。所以二分查找要求线性表必须采用顺序存储结构，而且表中元素按关键字有序排列。

二分查找思想：

    首先，假设表中元素是按升序排列，将表中间位置记录的关键字，与查找关键字比较，如果两者相等，则查找成功；否则利用中间位置记录将表分成前、后两个子表，如果中间位置记录的关键字大于查找关键字，则进一步查找前一子表，否则进一步查找后一子表。重复以上过程，直到找到满足条件的记录，使查找成功，或直到子表不存在为止，此时查找不成功。

    必须采用顺序存储结构。必须按关键字大小有序排列。

时间复杂度：O(logn)

方法一：查找算法设计为函数

例1 设计二分查找函数，从列表a = [80, 58, 73, 90, 31, 92, 39, 24, 14, 79, 46, 61, 31, 61, 93, 62, 11, 52, 34, 17]中查找31。

def binary_search(li, val):        # 二分查找函数
    left = 0
    right = len(li) - 1
    while left <= right:           # 候选区有值
        mid = (left + right) // 2
        if li[mid] == val:         # 如果循环都结束了，还没找到那就返回None
            return mid, li[mid]
        elif li[mid] > val:        # 待查找的值在mid左边
            right = mid - 1
        else:                      # 待查找的值在mid右边
            left = mid + 1

a=[80,58,73,90,31,92,39,24,14,79,46,61,31,61,93,62,11,52,34,17]  # 原始数据
a.sort()                           # 排序(默认升序)
jieguo = binary_search(a,31)       # 调用函数(a列表中找31)
print(jieguo)                      # 输出结果

执行结果：

(4, 31)

方法二：查找算法不用函数求

例2 设计二分查找算法(不用函数)，从列表a = [80, 58, 73, 90, 31, 92, 39, 24, 14, 79, 46, 61, 31, 61, 93, 62, 11, 52, 34, 17]中查找11。

a = [80, 58,73,90,31,92,39,24,14,79,46,61,31,61,93,62,11,52,34,17]  # 原始数据
a.sort()                               # 排序(默认升序)
left, right = 0, len(a) - 1
val = 11                               # a列表中找val
binary_search = None
while left <= right:                   # 候选区有值
    mid = (left + right) // 2
    if a[mid] == val:                  # 如果循环都结束了，还没找到那binary_search的初值None
        binary_search = mid, a[mid]
        break                          # 如果找到，结果赋给binary_search，并中断退出循环
    elif a[mid] > val:                 # 待查找的值在mid左边
        right = mid - 1
    else:                              # 待查找的值在mid右边
        left = mid + 1
print(binary_search)

执行结果：

(0, 11)

    类似的算法有二分法，一般数学上用于解方程的近似解。对于区间[a,b]上连续不断且f(a)·f(b)<0的函数y=f(x)，通过不断地把函数f(x)的零点所在的区间一分为二，使区间的两个端点逐步逼近零点，进而得到零点近似值的方法叫做二分法(bisection)。

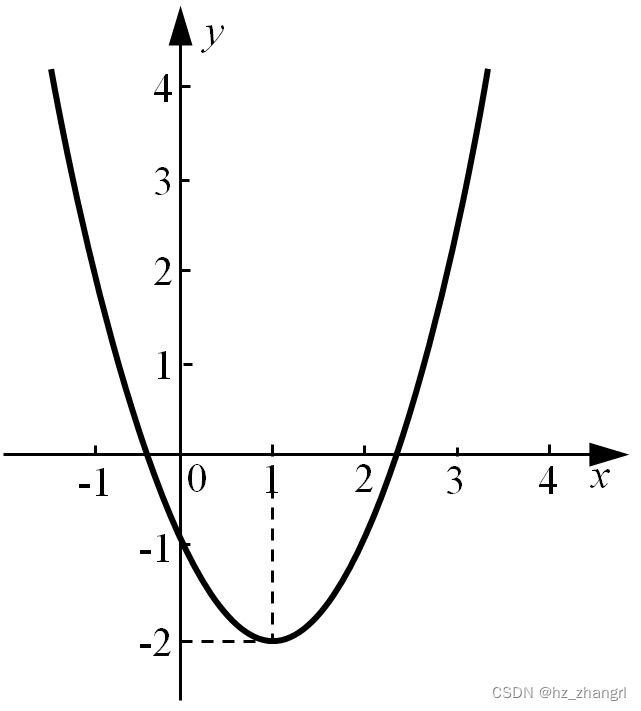
例3：用二分法求方程x²-2x-1=0的一个近似解(精确到0.00001)。

解：设f(x)= x²-2x-1

先画出函数图象的简图。(如图1所示)

图1 

    因为f(2)=-1<0，f(3)=2>0，所以在区间(2, 3)内，方程x²-2x-1=0有一解，记为x1。方程的数学解为：

用二分法求方程x²-2x-1=0的其中一个近似解的程序如下：

# 二分法求方程x²-2x-1=0的解
def f(x):                           # 输入x求f(x)
    return x**2-2*x-1

left = 2                            # 左区间f(left)=-1<0
right = 3                           # 右区间f(right)=2>0,[2,3]内有解
e = 0.00001                         # 精度要求
mid=(left+right)/2
while abs(f(mid))>e:                # 此处采用f(mid)来判断是否满足误差要求
    if f(left)*f(mid)<0:            # 说明区间[left,mid]内有解
        right = mid
    else:                           # 说明解在区间[mid,right]内
        left = mid
    mid = (left + right) / 2
print(mid)                          # 方程的解
print(f(mid))                       # 验证解的正确性

执行结果：

三、插值查找(插补查找)

    插值查找，又叫插补查找，英文名为Interpolation Search。

    插值查找类似于二分查找，是二分查找的改进。不过是通过预测的索引值进行分区，而不是简单的二分。

    首先考虑一个新问题，为什么二分查找算法一定要是二分，而不是四分之一分或者更多分呢？

    例如在查字典时，查“张”，就会查“弓”字旁，从“弓”字旁中查，不会从字典头翻到字典尾。

    同理，要在取值范围1~10000之间100个元素从小到大均匀分布的列表中查找5，自然会考虑从列表索引较小的开始查找。

     经过以上分析，二分查找方式，不是自适应的(也就是说是傻瓜式的)。二分查找中查找点计算如下：

mid=(left+right)/2, 即

mid=left+(right-left)/2= left+1/2*(right-left)                             ①

　　通过类比，我们可以将查找的点改进为如下：

mid=left+(key-a[left])/(a[right]-a[left])*(right-left)                    ②

式中：a是列表(或数组)，key是要想找的关键字。

    也就是将式①的比例参数1/2改进为自适应的(key-a[left])/(a[right]-a[left])，见式②。根据关键字在整个有序列表中所处的位置，让mid值的变化更靠近关键字key，这样就间接地减少了比较次数。

    基本思想：基于二分查找算法，将查找点的选择改进为自适应选择，可以提高查找效率。当然，插值查找也属于有序查找。

时间复杂度：O(logn)

例4 用插值查找从列表lst中想找tgt。完整程序如下：

标准插值查找完整程序如下：

def interpolation_search(lst, tgt):	# 定义插值查找函数
    left = 0						# 第一个lst元素的索引为0
    right = len(lst) - 1			# 最后一个lst元素的索引为元素个数-1
    found = False					# found=False表示还没找到
    while left <= right:
        mid = left + int((tgt-lst[left])/(lst[right]-lst[left])*(right-left))
        if lst[mid] == tgt:			# 第一种情况，mid对应的元素= tgt，找到退出循环
            found = True
            break
        else:
            if tgt < lst[mid]:		# 第二种情况，mid对应的元素>tgt，调右边界
                right = mid - 1
            else:					# 第三种情况，即mid对应的元素< tgt，调左边界
                left = mid + 1
    return found					# 返回查找结果

a = [80,58,73,90,31,92,39,24,14,79,46,61,31,61,93,62,11,52,34,17]	# 定义a
a.sort()
tgt1 = 84							# 定义要查找的目标元素1
print(interpolation_search(a, tgt1))	# 运行插值查找(从列表a查找tgt1)
lst2 = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20] 		# 定义lst2
tgt2 = 5							# 定义要查找的目标元素2
print(interpolation_search(lst2, tgt2))	# 运行插值查找(从列表lst2查找tgt2)

执行结果：

死机(死循环)

    经测试：(1)如查找的是列表中的元素，则正常。(2)如查找的不是列表中的元素，则可能出现死机(死循环)。

    经分析并查原因，发现当tgt

改进版完整程序如下：

def interpolation_search(lst, tgt):	# 定义插值查找函数
    left = 0						# 第一个lst元素的索引为0
    right = len(lst) - 1			# 最后一个lst元素的索引为元素个数-1
    found = False					# found=False表示还没找到
    if tgt < lst[left] or tgt > lst[right]:		# 查找值超范围，直接返回没找到
        return found
    
    while left <= right and tgt >= lst[left]:	# tgt >= lst[left]保证找不到时不“死循环”
        mid = left + int((tgt-lst[left])/(lst[right]-lst[left])*(right-left))
        if lst[mid] == tgt:			# 第一种情况，mid对应的元素= tgt，找到退出循环
            found = True
            break
        else:
            if tgt < lst[mid]:		# 第二种情况，mid对应的元素>tgt，调右边界
                right = mid - 1
            else:					# 第三种情况，即mid对应的元素< tgt，调左边界
                left = mid + 1
    return found					# 返回查找结果

a = [80,58,73,90,31,92,39,24,14,79,46,61,31,61,93,62,11,52,34,17]	# 定义a
a.sort()							# 排序
tgt1 = 84							# 定义要查找的目标元素1
print(interpolation_search(a, tgt1))			# 运行插值查找(从列表a查找tgt1)
lst2 = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20] 		# 定义lst2
tgt2 = 5							# 定义要查找的目标元素2
print(interpolation_search(lst2, tgt2))			# 运行插值查找(从列表lst2查找tgt2)

执行结果：

四、斐波那契查找

    在介绍斐波那契查找算法之前，我们先介绍一下很它紧密相连并且大家都熟知的一个概念——黄金比例。

    黄金比例又称黄金分割，是指事物各部分间一定的数学比例关系，即将整体一分为二，较大部分与较小部分之比等于整体与较大部分之比，其比值约为1:0.618或1.618:1。

    0.618被公认为最具有审美意义的比例数字，这个数值的作用不仅仅体现在诸如绘画、雕塑、音乐、建筑等艺术领域，而且在管理、工程设计等方面也有着不可忽视的作用。因此被称为黄金分割。

    斐波那契数列：1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…….(从第三个数开始，后边每一个数都是前两个数的和)。然后，随着斐波那契数列的递增，前后两个数的比值会越来越接近0.618，利用这个特性，我们就可以将黄金比例运用到查找技术中。

图2 

    基本思想：也是二分查找的一种提升算法，通过运用黄金比例的概念在数列中选择查找点进行查找，提高查找效率。同样地，斐波那契查找也属于一种有序查找算法。

    斐波那契查找与二分查找很相似，他是根据斐波那契序列的特点对有序表进行分割的。他要求开始表中记录的个数为某个斐波那契数小1，及n=F(k)-1;

 开始将k值与第F(k-1)位置的记录进行比较(及mid=left+F(k-1)-1),比较结果也分为三种

　　1)lst[mid] = tgt，mid位置的元素即为所求

　　2)lst[mid] < tgt，left=mid+1,k-=2;

    说明：left=mid+1说明待查找的元素在[mid+1,right]范围内，k-=2 说明范围[mid+1,right]内的元素个数为n-(F(k-1))= F(k)-1-F(k-1)=F(k)-F(k-1)-1=F(k-2)-1个，所以可以递归的应用斐波那契查找。

　　3)lst[mid] > tgt，right=mid-1,k-=1。

    说明：left=mid+1说明待查找的元素在[left,mid-1]范围内，k-=1 说明范围[left,mid-1]内的元素个数为F(k-1)-1个，所以可以递归的应用斐波那契查找。

    复杂度分析：最坏情况下，时间复杂度为O(logn)，且其期望复杂度也为O(logn)。

    斐波那契查找，是通过利用斐波那契数列的值作为分割点，然后二分查找，相对于普通的二分查找，性能更优秀。

例5 用斐波那契(Fibonacci)查找从列表lst中想找tgt。

完整程序如下：

fib = lambda n: n if n < 2 else fib(n-1) + fib(n-2) # 斐波那契函数

def fib_search(lst, x):
    if len(lst) == 0:
        return '列表是空的'
    left = 0
    right = len(lst) - 1
    # 求key值，fib(key)是大于等于lst的长度的，所以使用时要用key-1
    key = 0
    while fib(key) < len(lst):
        key += 1
    while left <= right:
        # 当x在分隔的后半部分时，fib计算的mid值可能大于lst长度
        mid = min(left + fib(key - 1) - 1, len(lst) - 1)
        if x < lst[mid]:
            right = mid - 1
            key -= 1
        elif x > lst[mid]:
            left = mid + 1
            key -= 2
        else:
            return mid
    return "没有找到"

a = [80,58,73,90,31,92,39,24,14,79,46,61,31,61,93,62,11,52,34,17]	# 定义a
a.sort()								# 排序(升序)
tgt1 = 84								# 定义要查找的目标元素1
print(fib_search(a, tgt1))
tgt2 = 62								# 定义要查找的目标元素1
print(fib_search(a, tgt2))

执行结果：