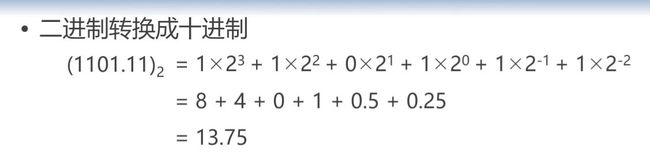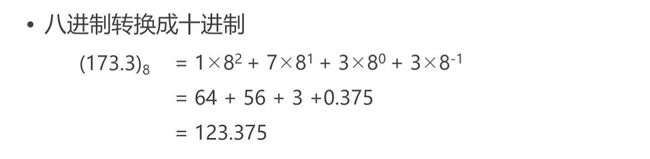进制转换(非常详细+算法代码)
——快开学了,进制转换忘了怎么办?
——没事,看这篇博客保你信手拈来 !
——学不会呢?
——****我!!
废话不多说,我们进入正题 :
常用的进制范围和其符号修饰:
二进制(B)————>0 ~ 1
八进制(O)————>0 ~ 7
十进制 (D) ————>0 ~ 9
十六进制(H)————>0 ~ 9 、A(10) ~ F(15)
R进制到十进制的转换
这一类的转换方法叫:按权展开求和
公式看不懂没关系,先看例子:
从例子中再去回看公式是不是就很easy了。
如果想证明一下自己,就练一下手吧:
10111.101B = 23.625D
7035O = 3613D
-8FD.C H= -2301.75D
当然最重要的还是如何将上述用代码实现:
这里我以python实现二进制转十进制为例,因为此类型都是一样的思想。
b=input("请输入一个二进制数:")
d=0;
for i in range(0,len(b)):
if b[i] == '1':
weight =2**(len(b)-i-1)
d+=weight;
print(d)
#当然如果你想进行小数的进制转换,其实和整数的转换思想是基本相同的
#你可以先用python自带的字符函数:partition()来找出小数点前面的字符串和小数点后面的字符串,
#例如:
# b="1101.01"
# (x,y,z) = b.partition('.') #结果是:x="1101" ,y="." ,z="01"
#然后对x和z分别转换再相加就可以了。
#注意对于z时,weight=2**(-i-1)当然c/c++的同学也要照顾的(>▽<):
#include
#include
using namespace std;
int main()
{
string s;
cin>>s;
int len=s.length();
int t=0;
double n;
for(int i=0;i 补充: 秦九韶算法:
for(int i = 0 ; i < len ; ++i ) // 这里只讨论了各种进制的整数部分转10进制
{
res = res * t + a[ i ] ; // t 表示待转换的进制数,比如二进制转10进制,t 就为 2 。
} a[ i ] 表示当前的待转进制数值。
len:表示此待转进制的长度。
注意:超过10进制,比如16进制转10进制,要注意0~9 和A(10)~ F(15)分开计算
十进制到R进制的转换
对于整数“除R取余”:
这里还是以十进制转二进制为例,其他则对比此思想。
代码实现如下:
x=int(input("请输入一个十进制整数: "))
r=0;
h=[];
while(x !=0 ):
r=x%2
x//=2
h=[r]+h
for i in range(0,len(h)):
print(h[i],end='')#include
using namespace std;
int j,x;
int main()
{
int h[1000]; //按题意要求,设置足够大即可,这里我用的数组,下文我还会使用字符串存
scanf("%d",&x);
while(x){
h[j++]=x%2;
x/=2;
}
for(int i=j-1;i>=0;--i){
printf("%d ",h[i]);
}
return 0;
} 对于小数 "乘R取整" :
注意这里代码实现的是小数部分的进制转换,如果求含整数和小数类型的,就分开求,再合并。
import math
k=eval(input("请输入十进制小数部分: "))
count=abs(k) #对k求绝对值
t=8 #保留位数的上限
N=0
while(t>0):
count=count*2
N=N*10+math.floor(count) #把求得的二进制拼上去
count-=math.floor(count) # 保留每次乘2后的小数部分
t-=1
N=N/100000000 #循环结束后得到的是整数,需要转变成原本的小数
if k>=0:
print(N)
else:
print(-N)#include
#include
using namespace std;
double k,N,t,count;
int main()
{
cin>>k;
count=abs(k);
N=0,t=8;
while(t>0){
count*=2;
N=N*10+floor(count);
count-=floor(count);
t-=1;
}
N/=100000000;
if(k>=0){
cout< ୧꒰•̀ᴗ•́꒱୨ 好了,复习到这里,是不是一下就充满信心了,哈哈~
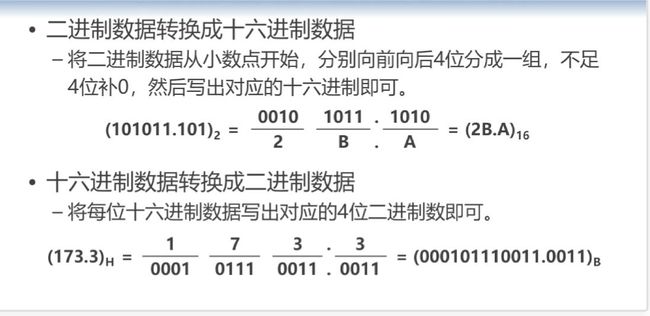
二、八、十六进制的巧妙转换
”三位一并法“ :
概念:以三位为一个单元划分二进制数,每个单元可以独立地转换为一个八进制数位。
你可以直接采用三位一并,当然也可以先将二进制转换成十进制(上面讲过),再将十进制转成八进制(上面讲过),就可以实现两者的转换,是不是一下就清晰明了了,哈哈,因此代码我就不写了,自己动手O(∩_∩)O
(三位一并法)python实现 :Python-八进制、二进制互转
这里我还是把c/c++的写一下吧,下面都是整数间的转换(不含小数),如果要求小数,就分个区分别求在合并。
//用三位一并法实现八进制转二进制:
#include
using namespace std;
string t[8] = {"000","001","010","011","100","101","110","111"}; //把对应的二进制罗列出来
string s,r="";
int main() {
cin>>s;
for(int i=0; i
using namespace std;
string s,k,c;
int r=0,t=1;
int main()
{
cin>>s; //读入二进制
//转十进制 (上文是正序循环,这里是逆序循环方法)
for(int i=s.size()-1;~i;--i){
r+=t*(s[i]-'0');
t*=2;
}
//转八进制 (上文是存数组中,这里我用字符串存)
while(r!=0){
c=r%8+'0'; //转字符
k=c+k; //注意k的位置要在c后面
r/=8;
}
if(k=="") cout<<0< “ 四位一并法 ”:
概念:以四位为一个单元划分二进制数,每个单元可以独立地转换为一个十六进制数位。
思想和上面是一样的,先将二进制转十进制,然后十进制转16进制,也可以直接采用四位一并法。
(四位一并法)python实现: Python-十六进制、二进制互转
//四位一并法将二进制转16进制
#include
using namespace std;
char nb(string k){
// 这不又又是二进制转十进制的方法嘛,hh
int r=0,t=1;
char m;
for(int i=k.size()-1;~i;--i){
r+=t*(k[i]-'0');
t*=2;
}
// 这里可要注意16进制的范围
if(r<10) m=r+'0';
else m=r+'A'-10;
return m;
}
int main()
{
string s,k;
cin>>s;
//先补0,便于四位一并转换
if(s.size()%4==1) s="000"+s;
else if(s.size()%4==2) s="00"+s;
else if(s.size()%4==1) s="0"+s;
for(int i=0;i
#include //引入 isdigit 函数(检测其参数是否为十进制数字字符)
#include //引入 pow 函数
using namespace std;
typedef long long LL;
const int N=1e6; //根据题目要求赋值大小
int a[N],r;
int main()
{
string s;
int p=0;
LL sum=0;
cin>>s;
//16进制转10进制
for(int i=s.size()-1;~i;--i){
if(isdigit(s[i])){
sum+=(s[i]-'0')*pow(16,p);
}
else sum+=(s[i]-'A'+10)*pow(16,p);
p++;
}
// 好了,现在又又回到了十进制转二进制了,hh
while(sum){
a[r++]=sum%2;
sum/=2;
}
for(int i=r-1;i>=0;--i){
printf("%d",a[i]);
}
return 0;
}
现在我们已经解决上面图片里除问号所有的进制转换,那八进制和十六进制怎么转换呢 ?
八进制和十六进制转换 :
从上面图片我们不难看出方法其实非常的简单,其实就是上面转换的”总结“。
那代码怎么实现呢?
当然先将十六进制数转换成某进制数,再由某进制数转换成八进制。
现在到这里你已经掌握了上面的方法,那就来尝试一下这道蓝桥杯 的进制转换题吧
(转换法)c/c++实现: 蓝桥杯:十六进制转八进制
结束语
到这里,非常感谢您的阅读,进制转换就基本复习完了,是不是信手拈来了,哈哈~
当然上述进制转换都是以算法代码实现的(主要是学习了解思想),转换后的值本质上还是十进制数
一般python都有进制转换的内置函数(严格意义上的进制转换),比如bin()、oct()、hex()............
更加详细介绍可参考:Python进制转换详细介绍
当然c\c++也有:【总结】C++各种进制转换函数汇总
C++ 二进制、十进制、八进制和十六进制 转换
目前大一在读,知识储备还比较低,如果这篇文章有不足的地方,请一定要在评论区指出来(学习并改正),如果这篇文章对你有帮助的话,不妨点赞+收藏+关注,我还会持续更新我的学习笔记,希望自己学习的同时,也能帮助他人୧꒰•̀ᴗ•́꒱୨ 。
函数介绍
༼ つ◕_◕ ༽つ
这里我再总结一下上述c/c++使用的函数,方便大家理解代码
length() 函数:用来获取字符串的长度( 统计\0 之前的字符个数 这里之前写错了,这是c库函数strlen()函数的特点,抱歉了)
size() 函数: c++中的size() 函数除了跟length一样可以获取字符长度之外,还可以获取vector类型的长度,这里我用了这两种方式,也能扩展一下知识。
pow(a , b) 函数: a的b次方,这里我方便表示次方才引用的
abs() 函数 :在c中只能对int整型生效,而在c++中对int、double、float 都支持对数据求绝对值
floor( x ) 函数 :把一个小数向下取整,通俗来说,就是不大于x的最大整数,比如2.6 就是 2 、-2.6 就是 -3
erase() 函数 :比如:string.erase(a,n) ,就是删除从a 开始的n 个字符
所以string.erase(0,1) 就是删除第一个字符,当然erase()函数还有更多用法,比如STL容器中,这里 不做阐述。
substr(a , n) 函数:上文是为了方便截取四位字符串,我才引用的这个函数,a表示提取字符串的开始位置, n 表示待提取的字符串长度,当然substr() 函数还有更多用法,比如还有替换字符串的功能。
isdigit() 函数 :检测其参数是否为十进制数字字符 。我认为这个函数还是蛮方便的,哈哈。当然利用ASCLL值对比也能检测的。
at( i ) 函数 :string.at() 函数主要用来获取指定字符和使用在STL中,i 表示想要获取的字符下标,函数返回值为指定的字符。at()函数一般比 [ ] 运算符更安全,它并不会去访问越界的元素,但其运行消耗时间更长。
上述我只是简要介绍了代码中使用的函数用法,主要是帮助大家理解,如果感兴趣的话可以自己去查这些函数的具体用法和注意事项。