Matlab求解线性方程组（一）共轭梯度法

一，算法原理

 共轭梯度法可以看作是特殊的迭代法，有迭代法的格式，即首先给出x(0),再由迭代格式

$x^{(k+1)}=x^{(k)}+{\alpha }_k{d}^{(k)}$

进行迭代，那么关键就是求出两个因素：方向$d^{(k)}$和步长${\alpha }_k$。

 首先确定最佳步长${\alpha }_k$，假设$x^{(k)}$和搜索方向$d^{(k)}$已给定，那么通过一元函数

$\varphi (\alpha )=f(x^{(k)}+{\alpha }_k{d}^{(k)})$

求极小值。令${\varphi }^{\prime }(\alpha )=0$ ($\alpha$ 为变量，其他为已知数)得到：

${\left[A\left(x^{(k)}+\alpha d^{(k)}\right)-b\right]}^T{d}^{(k)}=0$
${(-r^{(k)}+\alpha A{d}^{(k)})}^T{d}^{(k)}=0$

其中$r^{(k)}=b-A{x}^{(k)}$,由此解得最佳步长：

${\alpha }_{(k)}=\frac{r^{{(k)}^T}{d}^{(k)}}{d^{{(k)}^T}A{d}^{(k)}}$

 下面确定$d^{(k)}$，给定x(0)后，由于负梯度是函数下降最快的方向，故第一次迭代取搜索方向:

$d^{(0)}=r^{(0)}=b-A{x}^{(0)}$，

 由上式可算出x(1)。由x(1)出发的搜索方向不再取r(1)而是取

$d^{(1)}=r^{(1)}+{\beta }_0{d}^{(0)}$。
由于 $d^{(0)}$和 $d^{(1)}$为共轭向量，满足 $(d^{(1)}A{d}^{(0)})=0$，可求得 ${\beta }_0$并给出 ${\beta }_k$的一般表达式： ${\beta }_k=-\frac{r^{{(k+1)}^T}A{d}^{(k)}}{d^{{(k)}^T}A{d}^{(k)}}$

再由$d^{(k+1)}=r^{(k+1)}+{\beta }_k{d}^{(k)}$算出$d^{(k\text{+}1)}$。

综上所述得出共轭梯度法的计算公式：

$\{\begin{array}{l}{d}^{(0)}=r^{(0)}=b-A{x}^{(0)}\\ {\alpha }_k=\frac{r^{{(k)}^T}{d}^{(k)}}{d^{{(k)}^T}A{d}^{(k)}}\\ x^{(k+1)}=x^{(k)}+{\alpha }_k{d}^{(k)}\\ r^{(k+1)}=b-A{x}^{(k+1)}\\ {\beta }_k=-\frac{r^{{(k+1)}^T}A{d}^{(k)}}{d^{{(k)}^T}A{d}^{(k)}}\\ d^{(k+1)}=r^{(k+1)}+{\beta }_k{d}^{(k)}\end{array}$

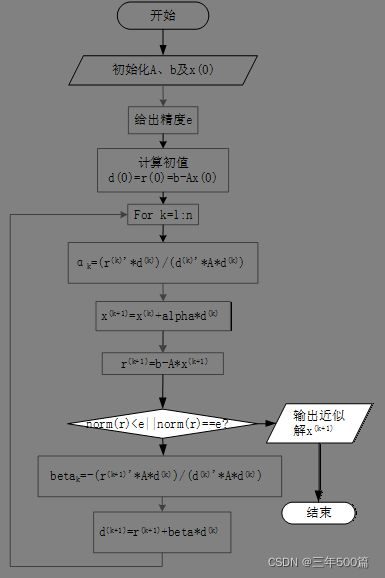
二，程序框图

三，源代码

1，主函数（实现共轭梯度求解方程组）

%共轭梯度法求线性方程组
%   'A';系数矩阵
%   'b':右端项
%   'e0':求解精度
function [error,x]=gongetidu(A,b,e0)
%给定初始向量x0和计算精度e0,error代表误差。
n=length(b);
x=zeros(n,1);
r=b-A*x;				%r为误差
d=r;					%d为搜索方向
i=1;
for k=1:n
    alpha=(r'*d)/(d'*A*d);
    x=x+alpha*d;
    r1=b-A*x; 
    error(i)=norm(r1);
    bt=-(r1'*A*d)/(d'*A*d);
    d=r1+bt*d;
    r=r1;
    i=i+1;
    if norm(r1)<=e0
        break;
    end
end

2，建立课本计算实习3.2方程组的系数矩阵及右端项

%建立课本计算实习3.2方程组的系数矩阵及右端项
function [A,b]=build(n)
A=zeros(n,n);
b=zeros(n,1);
b(1)=-1;
b(n)=-1;
for i=1:n
    A(i,i)=-2;
end
for j=1:n-1
    A(j,j+1)=1;
end
for j=2:n
    A(j,j-1)=1;
end

四，实例分析

计算实例P113：用共轭梯度法求解线性方程组Ax=b，其中

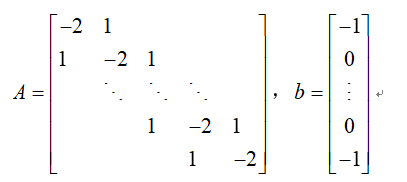
矩阵A的阶数n分别取为100，200，400，指出计算结果是否可靠。
解：输入以下代码

clc;
clear;
n=input('Please input n:');				%输入矩阵A的阶数
e0=input('Please input the accuracy:');
[A,b]=build(n);						%建立课本例3.2方程组系数矩阵及右端项
[error,x]=gongetidu(A,b,e0);             %使用共轭梯度法进行迭代求解
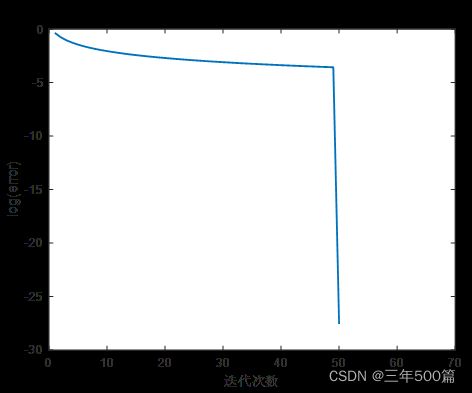
q=log(error);
plot(q,'linewidth',1.5)
xlabel('迭代次数');
ylabel('log(error)');
title('共轭梯度法迭代误差变化曲线');

例，n=100时，迭代50次后满足精度要求，其误差曲线如下图所示。