树与二叉树(详解定义性质基本操作,附代码和选择题)
文章目录
- 树
-
- 定义
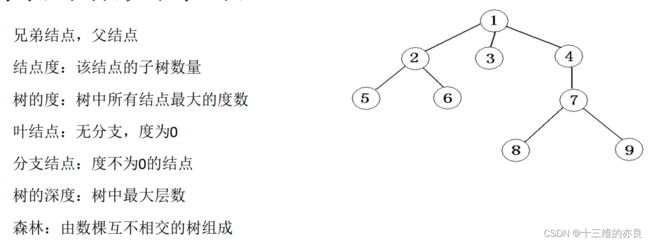
- 相关术语
- 二叉树
-
- 定义
- 分类
- 性质
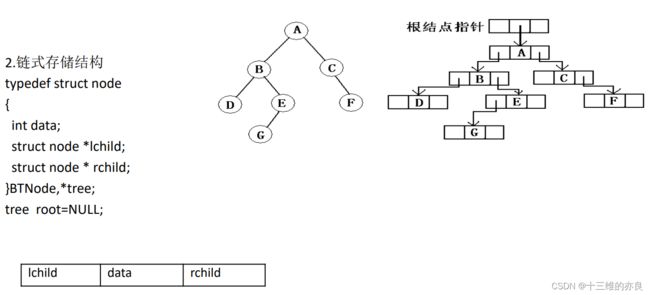
- 存储
- 基本操作
-
- 1.建立一棵二叉树
- 2.二叉树的遍历
- 3.删除一棵二叉树
- 4.求k层结点的个数
- 5.二叉树某结点的层数
- 6.判断一棵二叉树是否为完全二叉树
- 7.判断一棵二叉树是否为搜索二叉树
- 8.插入一个结点到搜索二叉树中
- 9.在搜索二叉树中查找一棵树
- 10.等等...
- 一些知识点
-
- 已知中序序列和先序/后序序列,构造出二叉树
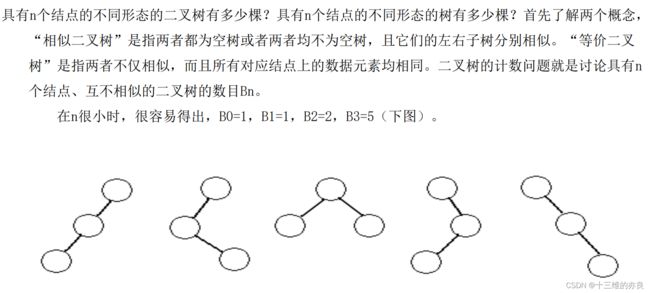
- 树的计数问题
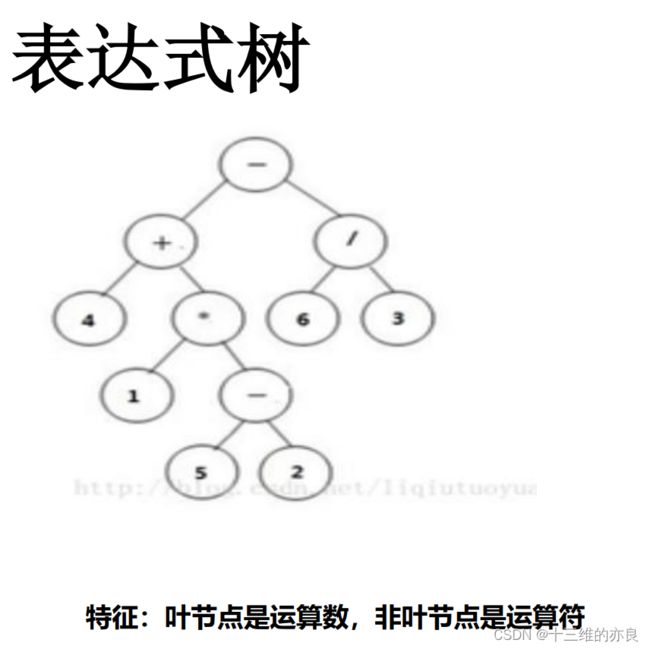
- 表达式树
- 相关选择题
树
定义
相关术语
二叉树
定义
分类
性质
存储
基本操作
1.建立一棵二叉树
void pre_crt(tree &bt) { //按先序次序输入二叉树中结点的值,生成
char ch;
ch = getchar(); //二叉树的单链表存储结构,bt为指向根结点的指针,'$'表示空树
if(ch != '$') {
bt = new node; //建根结点
bt->data = ch;
pre_crt(bt->lchild); //建左子树
pre_crt(bt->rchild); //建右子树
}
else bt = NULL;
}
2.二叉树的遍历
先序遍历(DLR):
若二叉树为空,则空操作,否则
①访问根结点
②先序遍历左子树
③先序遍历右子树
void DLR(tree bt) {
if(bt == NULL) return;
cout << bt -> data;
DLR(bt -> lchild);
DLR(bt -> rchild);
}
中序遍历(LDR):
若二叉树为空,则空操作,否则
①中序遍历左子树
②访问根结点
③中序遍历右子树
void LDR(tree bt) {
if(bt == NULL) return;
LDR(bt -> lchild);
cout << bt -> data;
LDR(bt -> rchild);
}
后序遍历(LRD):
若二叉树为空,则空操作,否则
①后序遍历左子树
②后序遍历右子树
③访问根结点
void LRD(tree bt) {
if(bt == NULL) return;
LRD(bt -> lchild);
LRD(bt -> rchild);
cout << bt -> data;
}
层序遍历(BTLevelSearch)
①首先判断根节点是否为NULL,若是则直接return
②将二叉树的根节点push到队列中
③输出队头的值,并用tmp将队头保存下来,队头出队
④判断队头节点是否有左右孩子,若有则将孩子push到队列中
⑤循环以上操作,直到队空
void BTLevelSearch(tree bt) {
queue <tree> q;
if (bt == NULL) return;
//根节点入队
q.push(bt);
//维护队列
while (!q.empty()) {
//记录队头,队头出队
tree tmp = q.front();
cout << tmp -> data;
q.pop();
//可扩展点入队
if (tmp -> lchild) q.push(tmp -> lchild);
if (tmp -> rchild) q.push(tmp -> rchild);
}
}
#include3.删除一棵二叉树
void dis(tree &bt) {//删除二叉树
if(bt != NULL) {
dis(bt->lchild); //删左子树
dis(bt->rchild); //删右子树
free(bt); //释放父结点
}
}
4.求k层结点的个数
int BTNodeKLevel(tree bt, int k) { //求k层结点的个数
if (bt == NULL) return 0;
if (k == 1) return 1;
return BTNodeKLevel(bt -> lchild, k - 1) + BTNodeKLevel(bt -> rchild, k - 1);
}
5.二叉树某结点的层数
void getNodeLayer(tree root,int x,int layer) {
if(root == NULL) return;
if(root->data == x) {
cout << layer << endl;
return;
}
getNodeLayer(root->lchild, x, layer + 1);
getNodeLayer(root->rchild, x, layer + 1);
}
6.判断一棵二叉树是否为完全二叉树
借助queue,将各个结点,以层序遍历序列进入队列(与二叉树的层序遍历不同的是,值为NULL的结点也需要入队)。
如果发现队头为NULL,表示我们读到了一个空节点,如果它后面的结点都是NULL,则该二叉树是完全二叉树;如果它后面的结点有非NULL结点,则该二叉树不是完全二叉树。

bool BTComplete(tree bt) { //判断是否为完全二叉树
queue <tree> q;
if (bt == NULL) return true;
//根节点入队
q.push(bt);
//维护队列
while (!q.empty()) {
tree tmp = q.front();
if (tmp == NULL) { //找到NULL,那么就看其后是否有非NULL结点
while (!q.empty()) {
if (q.front()) return false; //找到非NULL结点,返回false
q.pop();
}
return true; //没有非NULL结点,返回true
}
else { //还没有找到NULL,继续找
q.push(tmp -> lchild);
q.push(tmp -> rchild);
}
q.pop();
}
}
7.判断一棵二叉树是否为搜索二叉树
//中序遍历二叉树,采用递归方法
void mid_order(tree root, vector<char> &v1) {
if(root == NULL) return;
mid_order(root -> lchild, v1);//先遍历左子树
v1.push_back(root -> data); //然后遍历根节点,将值存储在vector中
mid_order(root -> rchild, v1);//再遍历右子树
}
bool isValidBST(tree root) {
if(root == NULL) return true;
vector<char> v;
mid_order(root,v);
int size = v.size();
for(int i = 0; i < size - 1 ; ++i) {
if(v[i] >= v[i + 1])//不符合升序,或者存在重复,返回false
return false;
}
//经中序遍历后为无重复的升序序列,则是二叉搜索树
return true;
}
8.插入一个结点到搜索二叉树中
void insert(tree &bt, int n) { //插入一个结点到搜索二叉树中
if(bt) {
if(n < bt -> data) insert(bt -> lchild, n);
else if(n > bt -> data) insert(bt -> rchild, n);
}
else {
bt = new node; //新开一个空间
bt->data = n;
bt->lchild = bt->rchild = NULL;
}
}
9.在搜索二叉树中查找一棵树
tree findn(tree bt, int n) { //在排序二叉树中查找一个数,找到返回该结点,否则返回NULL。
if(bt == NULL) return NULL;
if(n < bt->data) findn(bt->lchild, n);
else if(n > bt->data) findn(bt->rchild, n);
else return bt;
}