数据结构——二叉树的先中后序遍历
——本节内容为Bilibili王道考研《数据结构》P43~P45视频内容笔记。
目录
一、二叉树的先中后序遍历
1.先中后序遍历
2.举例
3.先中后序遍历和前中后缀的关系
4.代码实现
5.求遍历序列
6.应用:求树的深度
二、二叉树的层次遍历
1.层次遍历
2.算法思想:
3.算法演示:
4.代码实现:
三、由遍历序列构造二叉树
1.遍历序列构造二叉树
2.前序+中序
3.后序+中序
4.层序+中序
一、二叉树的先中后序遍历
1.先中后序遍历
(1)二叉树的递归特性:
①要么是个空二叉树;
②要么是由“根结点+左子树+右子树”组成的二叉树。
(2)基于此,给出三种遍历方式:
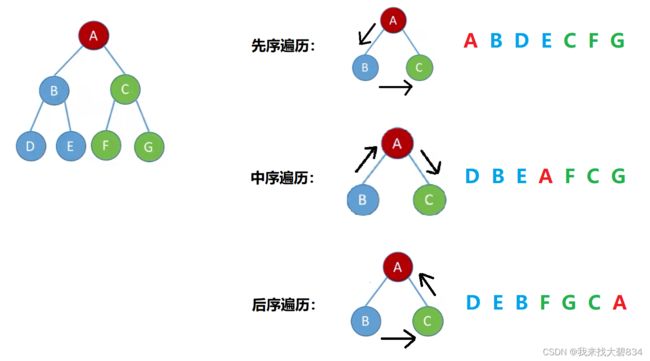
①先序遍历(先根遍历):根左右(NLR)
②中序遍历(中根遍历):左根右(LNR)
③后序遍历(后根遍历):左右根(LRN)
(3)先序遍历、中序遍历、后序遍历
①先序遍历:
先访问根结点,再访问该根结点的左子树结点,最后访问该根结点的右子树结点;如果其左子树或右子树为分支结点,则需要对分支结点再进行一遍先序遍历,这种访问方式也是一种递归方式。
②中序遍历:
先访问根结点的左子树结点,再访问根结点,最后访问根结点的右子树结点;如果其左子树或右子树为分支结点,则需要对分支结点再进行一遍中序遍历。
③后序遍历:
先访问根结点的左子树结点,再访问根结点的右子树结点,最后访问根结点;如果其左子树或右子树为分支结点,则需要对分支结点再进行一遍后序遍历。
2.举例
3.先中后序遍历和前中后缀的关系
(1)先来看一个例子:
(2)求其先中后序遍历遍历序列分别为:
①先序遍历:![]() ;
;
②中序遍历:![]() ;
;
③后序遍历:![]() ;
;
(3)求其前中后缀表达式:
①前缀表达式:![]() ;
;
②中缀表达式:![]() ;
;
③后缀表达式:![]() ;
;
(4)观察(2)(3)可得在算术表达式“分析树”中所得到的先中后序遍历即为该算术表达式的前中后缀表达式,只不过其中中缀表达式要自己加界限符。
4.代码实现
(1)先序遍历代码:
若二叉树为空,则什么也不做;
若二叉树非空:①访问根结点;
②先序遍历左子树;
③先序遍历右子树。
typedef struct BiTNode {
int data;
struct BiTNode* lchild, * rchild;
}BiTNode,*BiTree;
void PreOrder(BiTree T)
{
if (T != NULL)
{
visit(T); 访问根结点,visit()执行相关访问操作的函数,比如打印...
PreOrder(T->lchild); //递归遍历左子树
PreOrder(T->rchild); //递归遍历右子树
}
}
(2)中序遍历代码:
若二叉树为空,则什么也不做;
若二叉树非空:①中序遍历左子树;
②访问根结点;
③中序遍历右子树。
void InOrder(BiTree T)
{
if (T != NULL)
{
InOrder(T->lchild); //递归遍历左子树
visit(T); //访问根结点
InOrder(T->rchild); //递归遍历右子树
}
}(3)后序遍历代码:
若二叉树为空,则什么也不做;
若二叉树非空:①后序遍历左子树;
②后序遍历右子树;
③访问根结点。
void PostOrder(BiTree T)
{
if (T != NULL)
{
PostOrder(T->lchild); //递归遍历左子树
PostOrder(T->rchild); //递归遍历右子树
visit(T); //访问根结点
}
}5.求遍历序列
(1)求先序遍历序列
(2)求中序遍历序列
(3)求后序遍历序列
6.应用:求树的深度
后序遍历算法变种之求树的深度:
int treeDepth(BiTree T)
{
if (T == NULL)
return 0;
else
{
int l = treeDepth(T->lchild);
int r = treeDepth(T->rchild);
return l > r ? l + 1 : r + 1; //树的深度=Max(左子树深度,右子树深度)+1
}
}二、二叉树的层次遍历
1.层次遍历
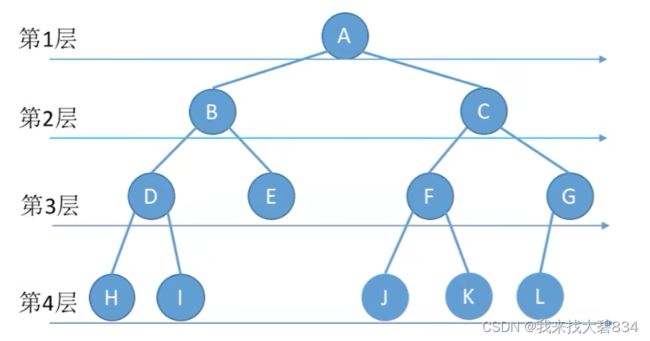
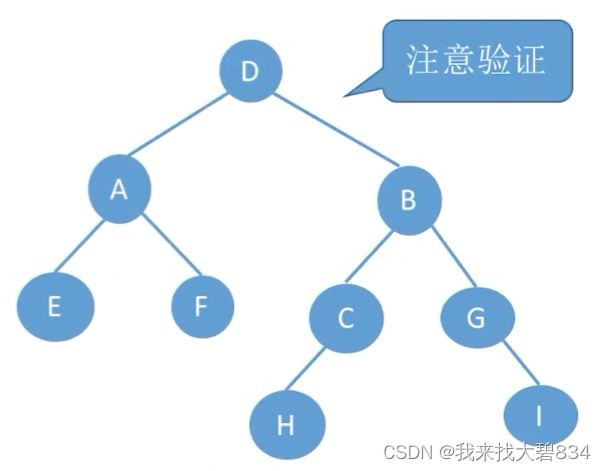
如图所示,层次遍历即一层一层访问数的结点:A B C D E F G H I J K L;
2.算法思想:
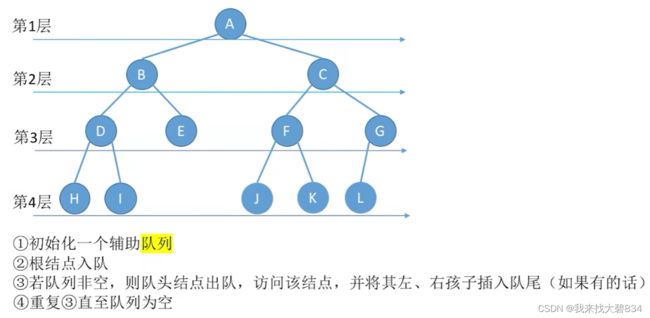
(1)初始化一个辅助队列;
(2)根结点入队;
(3)若队列非空,则队头结点出队,并访问该结点,然后将其左、右子树结点插入队尾(如果有的话)。
3.算法演示:
4.代码实现:
//二叉树的结点(链式存储)
typedef struct BiTNode {
char data;
struct BiTNode* lchild, * rchild;
}BiTNode,*BiTree;
//链式队列结点
typedef struct LinkNode {
BiTNode* data; //存指针而不是结点,节省内存空间
struct LinkNode* next;
}LinkNode;
typedef struct {
LinkNode* front, * rear; //队头队尾指针
}LinkQueue;
//层序遍历
void LevelOrder(BiTree T)
{
LinkQueue Q;
InitQueue(Q); //初始化辅助队列
BiTree p;
EnQueue(Q, T); //将根结点入队
while (!IsEmpty(Q)) //队列不空则循环
{
DeQueue(Q, p); //对头结点出队
visit(p); //访问出队结点
if (p->lchild != NULL)
EnQueue(Q, p->lchild); //左孩子入队
if (p->rchild != NULL)
EnQueue(Q, p->rchild); //右孩子入队
}
}三、由遍历序列构造二叉树
1.遍历序列构造二叉树
(1)若只给出一棵二叉树的前/中/后/层序遍历中的一种,不能确定唯一一棵二叉树。
(2)由遍历序列构造二叉树需要:
①前序+中序遍历序列;
或②后序+中序遍历序列;
或③层序+中序遍历序列;
2.前序+中序
(1)方法:
①由前序遍历序列判断出根结点;
②由根结点在中序遍历序列中的位置判断出左子树和右子树的前序和中序遍历序列;
③分别对左右子树的前序和中序遍历序列再进行①②的分析判断出所有的结点;
(2)举例:
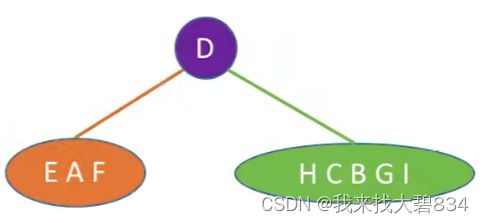
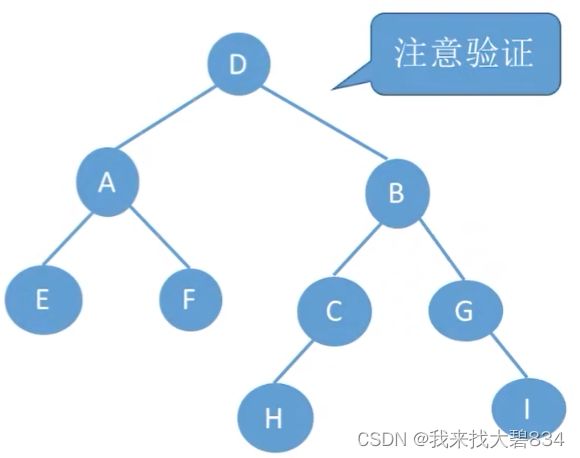
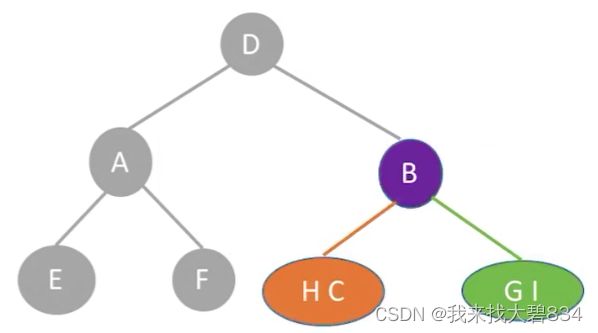
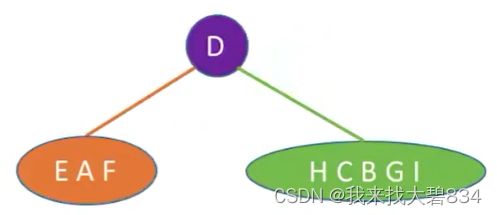
①由前序遍历序列第一个D判断出D为根结点,其所在中序遍历序列的位置判断出:
左子树中序序列:EAF;前序序列:AEF;
右子树中序序列:HCBGI;前序序列:BCHGI;
如下图:
②由左子树前序序列判断左子树根结点为A,由其所在左子树中序序列的位置判断出:
根结点A的左子树为E;右子树为F;
③由右子树前序序列判断右子树根结点为B,由其所在右子树中序序列的位置判断出:
根结点B的左子树中序序列为HC;前序序列为CH;
根结点B的右子树中序序列为GI;前序序列为GI;
如下图:
④由所示橘色结点的前序序列CH判断这里的根结点为C;由C所在中序序列的位置判断出H为C的左子树结点;
⑤由所示绿色结点的前序序列GI判断这里的根结点为G;由G所在中序序列的位置判断出I为G的右子树结点;
如下图:
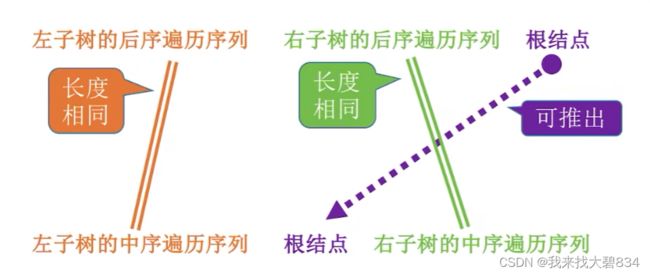
3.后序+中序
(1)方法
①由后序遍历序列判断出根结点;
②由根结点在中序遍历序列中的位置判断出左子树和右子树的后序和中序遍历序列;
③分别对左右子树的后序和中序遍历序列再进行①②的分析判断出所有的结点;
(2)举例:
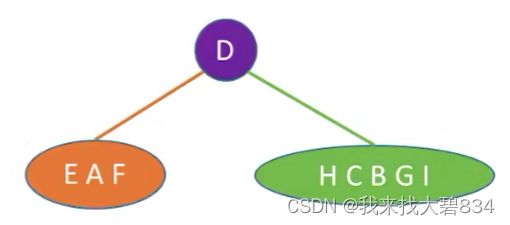
①由后序遍历序列判断出根结点为D;由D在中序序列的位置判断出:
D的左子树中序序列:EAF;后序序列:EFA;
D的右子树中序序列:HCBGI;后序序列:HCIGB;
如下图:
②由图中橘色部分后序序列EFA判断出这里的根结点为A;由A在中序序列EAF所在位置判断出A的左子树结点为E,右子树结点为F;
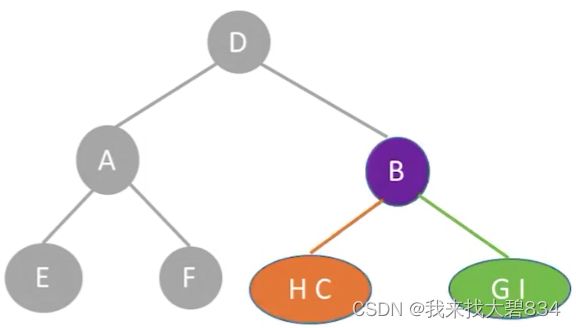
③由图中绿色部分后序序列HCIGB判断出这里的根结点为B;由B在中序序列HCBGI所在位置判断出:
B的左子树结点的中序序列:HC;后序序列:HC;
B的右子树结点的中序序列:GI;后序序列:IG;
如下图:
④由橘色部分后序序列HC判断这里的根结点为C,由C在中序序列的位置判断H为C的左子树结点;
⑤由绿色部分后序序列IG判断这里的根结点为G,由G在中序序列的位置判断I为G的右子树结点;
如下图:
4.层序+中序
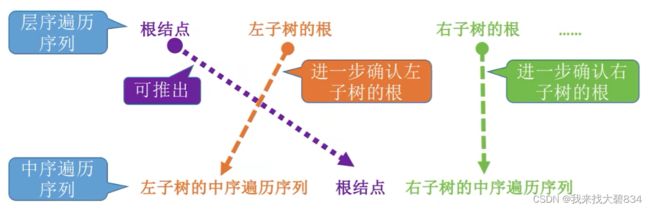
(1)方法:
①由层序遍历序列判断根结点;
②由根结点在中序序列中的位置判断根结点的左右子树的中序序列(注意可能会有空树的情况);
③由层序遍历序列判断下一层的根结点;
④由下一层根结点在中序序列中的位置判断下一层根结点的左右子树的中序序列(注意空树);
⑤反复以上分析,判断出所有的结点;
(2)举例:
①由层序遍历序列判断D为根结点;由D所在中序序列中的位置判断:
D的左子树中序序列:EAF;右子树中序序列:HCBGI;
如下图:
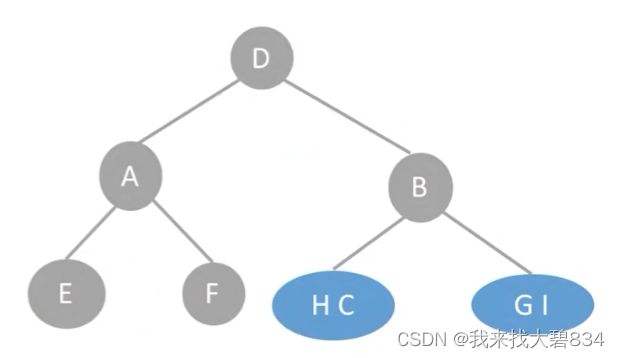
②由层序遍历序列判断第二层的根结点分别为A和B;由A和B在中序序列中的位置判断:
A的左子树结点为E,右子树结点为F;
B的左子树中序序列为HC,右子树中序序列为GI;
如下图:
③上图所示,第三层分别为:E、F、HC中出一个、GI中出一个;
④由层序序列判断HC中出C,GI中出G;
⑤最后由中序序列判断H为C的左子树结点;I为G的右子树结点,如下图: