PyG基于DeepWalk实现节点分类及其可视化

---

前言

大家好，我是阿光。

本专栏整理了《图神经网络代码实战》，内包含了不同图神经网络的相关代码实现（PyG以及自实现），理论与实践相结合，如GCN、GAT、GraphSAGE等经典图网络，每一个代码实例都附带有完整的代码。

正在更新中~ ✨

我的项目环境：

• 平台：Windows10
• 语言环境：python3.7
• 编译器：PyCharm
• PyTorch版本：1.11.0
• PyG版本：2.1.0

项目专栏：【图神经网络代码实战目录】

---

本文我们将使用Pytorch + Pytorch Geometric来简易实现一个DeepWalk，让新手可以理解如何PyG来搭建一个简易的图网络实例demo。

一、导入相关库

本项目我们需要结合两个库，一个是Pytorch，因为还需要按照torch的网络搭建模型进行书写，第二个是PyG，因为在torch中并没有关于图网络层的定义，所以需要torch_geometric这个库来定义一些图层。

import matplotlib.pyplot as plt
import torch
from sklearn.manifold import TSNE
from torch_geometric.datasets import Planetoid
from torch_geometric.nn import Node2Vec

二、加载Cora数据集

本文使用的数据集是比较经典的Cora数据集，它是一个根据科学论文之间相互引用关系而构建的Graph数据集合，论文分为7类，共2708篇。

• Genetic_Algorithms
• Neural_Networks
• Probabilistic_Methods
• Reinforcement_Learning
• Rule_Learning
• Theory

这个数据集是一个用于图节点分类的任务，数据集中只有一张图，这张图中含有2708个节点，10556条边，每个节点的特征维度为1433。

# 1.加载Cora数据集
dataset = Planetoid(root='./data/Cora', name='Cora')

本项目是使用 Node2Vec 来生成每个节点的特征，所以对于原始节点特征是无用的，本项目只是单纯利用 Cora 数据集的节点空间关系，也就是 edge_index ，基于节点的空间关系来生成对应的节点特征，最终验证生成的节点特征效果如何。

三、定义DeepWalk

这里我们就不重点介绍DeepWalk了，相信大家能够掌握基本原理，本文我们使用的是PyG定义这个网络，在PyG中已经定义好了 Node2Vec 这个层，我们可以利用这个层来实现 DeepWalk 。

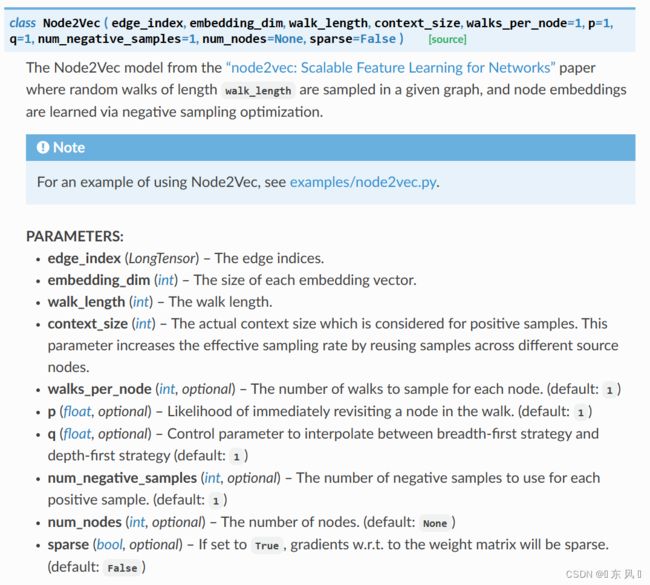
对于Node2Vec的常用参数：

• edge_index：图数据中的边关系，就是 data 的 edge_index，形状为【2，num_edges】
• embedding_dim：每个节点形成的嵌入维度
• walk_length：游走形成的序列长度
• context_size：上下文大小
• walks_per_node：每个节点形成多少个游走序列
• p：在游走时重新访问某个节点的概率，默认为1
• q：在BFS策略和DFS策略之间的控制参数，默认为1
• num_negative_samples：每个正样本对应的负样本数，默认为1
• num_nodes：图的节点数目
• sparse：如果设置为True，权重矩阵的梯度是以稀疏矩阵方式存储，默认为False

如果熟悉 DeepWalk 和 Node2Vec 两个算法的小伙伴可以发现，如果把 Node2Vec 在游走时设置的概率 p 和 q 同时设为1，此时 Node2Vec 就会退化成为 DeepWalk 。

# deepwalk模型
model = Node2Vec(edge_index=data.edge_index,
                 embedding_dim=128, # 节点维度嵌入长度
                 walk_length=5, # 序列游走长度
                 context_size=4, # 上下文大小
                 walks_per_node=1, # 每个节点游走10个序列
                 p=1,
                 q=1,
                 sparse=True # 权重设置为稀疏矩阵
                ).to(device)

对于模型训练等部分，与 Node2Vec 实现方式一致，所以这里不再赘述，如果不清楚的小伙伴可以先去查看本传内的这篇文章 PyG基于Node2Vec实现节点分类及其可视化，这篇文章详细介绍了代码实战部分。

四、可视化

上面我们以经训练好了 DeepWalk 这个模型，通过调用 model() 即可获得内部的权重矩阵，也就是我们要的Embedding向量表（lookup table）。

生成好每个节点的 Embedding，我们可以通过可视化的方式更加直观的看到效果如何，对于可视化操作我们利用的是 TSNE 这个模块来进行降维，因为绘制二维图形需要x轴和y轴坐标（即二维），降到两个维度后，就获得了每个节点的坐标信息，然后利用 matplotlib 这个库来绘制不同类别的节点信息。

# 可视化节点的embedding
with torch.no_grad():
    # 不同类别节点对应的颜色信息
    colors = [
            '#ffc0cb', '#bada55', '#008080', '#420420', '#7fe5f0', '#065535',
            '#ffd700'
        ]

    model.eval() # 开启测试模式
    # 获取节点的embedding向量，形状为[num_nodes, embedding_dim]
    z = model(torch.arange(data.num_nodes, device=device))
    # 使用TSNE先进行数据降维，形状为[num_nodes, 2]
    z = TSNE(n_components=2).fit_transform(z.detach().numpy())
    y = data.y.detach().numpy()

    plt.figure(figsize=(8, 8))
    
    # 绘制不同类别的节点
    for i in range(dataset.num_classes):
        # z[y==0, 0] 和 z[y==0, 1] 分别代表第一个类的节点的x轴和y轴的坐标
        plt.scatter(z[y == i, 0], z[y == i, 1], s=20, color=colors[i])
    plt.axis('off')
    plt.show()

完整代码

import matplotlib.pyplot as plt
import torch
from sklearn.manifold import TSNE
from torch_geometric.datasets import Planetoid
from torch_geometric.nn import Node2Vec

# 1.加载Cora数据集
dataset = Planetoid(root='../data/Cora', name='Cora')
data = dataset[0]

# 2.定义模型
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu') # 设备

# deepwalk模型
model = Node2Vec(edge_index=data.edge_index,
                 embedding_dim=128, # 节点维度嵌入长度
                 walk_length=5, # 序列游走长度
                 context_size=4, # 上下文大小
                 walks_per_node=1, # 每个节点游走1个序列
                 p=1,
                 q=1,
                 sparse=True # 权重设置为稀疏矩阵
                ).to(device)

# 迭代器
loader = model.loader(batch_size=128, shuffle=True)
# 优化器
optimizer = torch.optim.SparseAdam(model.parameters(), lr=0.01)

# 3.开始训练
model.train()

for epoch in range(1, 101):
    total_loss = 0 # 每个epoch的总损失
    for pos_rw, neg_rw in loader:
        optimizer.zero_grad()
        loss = model.loss(pos_rw.to(device), neg_rw.to(device)) # 计算损失
        loss.backward()
        optimizer.step()
        total_loss += loss.item()
    
    # 使用逻辑回归任务进行测试生成的embedding效果
    with torch.no_grad():
        model.eval() # 开启测试模式
        z = model() # 获取权重系数，也就是embedding向量表
        
        # z[data.train_mask] 获取训练集节点的embedding向量
        acc = model.test(z[data.train_mask], data.y[data.train_mask],
                         z[data.test_mask], data.y[data.test_mask],
                         max_iter=150) # 内部使用LogisticRegression进行分类测试
    
    # 打印指标
    print(f'Epoch: {epoch:02d}, Loss: {total_loss:.4f}, Acc: {acc:.4f}')

# 可视化节点的embedding
with torch.no_grad():
    # 不同类别节点对应的颜色信息
    colors = [
            '#ffc0cb', '#bada55', '#008080', '#420420', '#7fe5f0', '#065535',
            '#ffd700'
        ]

    model.eval() # 开启测试模式
    # 获取节点的embedding向量，形状为[num_nodes, embedding_dim]
    z = model(torch.arange(data.num_nodes, device=device))
    # 使用TSNE先进行数据降维，形状为[num_nodes, 2]
    z = TSNE(n_components=2).fit_transform(z.detach().numpy())
    y = data.y.detach().numpy()

    plt.figure(figsize=(8, 8))
    
    # 绘制不同类别的节点
    for i in range(dataset.num_classes):
        # z[y==0, 0] 和 z[y==0, 1] 分别代表第一个类的节点的x轴和y轴的坐标
        plt.scatter(z[y == i, 0], z[y == i, 1], s=20, color=colors[i])
    plt.axis('off')
    plt.show()