图机器学习--DeepWalk&Node2Vec
DeepWalk&Node2Vec
- 1.DeepWalk、
-
- 1.1 deepwalk官方:
-
- 1.1.1 提取特征
- 1.1.2 语言模型
- 1.1.3 deepwalk
- 1.1.4 评估
- 1.1.5 展望
- 1.2 讨论
- 1.3 DeepWalk论文精读
-
- 1.3.1 Introduction
- 1.3.2 问题描述
- 1.3.3 学习社会表示
- 1.3.4 算法
- 1.3.5 算法变种
- 1.3.6 实验
- 2 Node2Vec
-
- 2.1 讨论
- 2.2 论文精读
-
- 2.2.1 特征学习框架
- 2.2.2 算法
- 2.2.3 伪代码
- 2.2.4 node embedding 扩展到link embedding
1.DeepWalk、
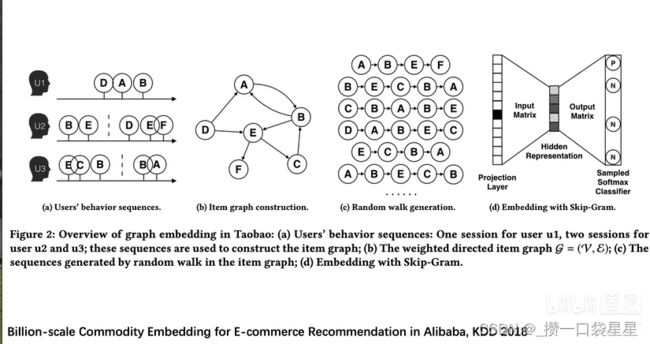
把word2vec应用到图中
一个醉汉在图中随机游走，采样出若干个随机序列。
假设：相邻节点应该具有相似地embedding
解决图嵌入问题，将节点编码为d维向量（无监督学习）
图嵌入中隐式包含了graph中的社群、连接、结构信息，可用于节点分类等下游任务（监督学习）
Skip-gram 和 CBOW 模型是两种常用的word2vec的模型
如果是用一个词语作为输入，来预测它周围的上下文，那这个模型叫做『Skip-gram 模型』
而如果是拿一个词语的上下文作为输入，来预测这个词语本身，则是 『CBOW 模型』
与word2vec类似，用节点1预测周围节点就是Skip-gram 模型
机器语言无法识别语言，需要将句子或者单词编码为向量
下图目标：将词编码为向量，可以反映词与词之间的关系（性别关系、时态关系、国家和首都的关系）
『Skip-gram 模型』：中心词预测周围词
『CBOW 模型』：周围词预测中心词。
为什么要用周围词预测中心词？：因为，word2vec的假设是临近词是相似的，相关联的。因此可以自监督地有效提取词向量。这些词向量可以反映相似性。
以Skip-gram 模型为例：
1.1 deepwalk官方:
1.1.1 提取特征
降维
优点：
- 可扩展，增量学习。在线学习算法，新加入节点后无须重新训练，只须把新的关联数据采样下来增量训练即可
- 套用自然语言模型
- 效果不错，特别是在稀疏标注的图分类任务上
1.1.2 语言模型
词嵌入是热点研究
词频呈现长尾分布或二八分布：少部分词出现的频率很高，大部分词出现的频率很低
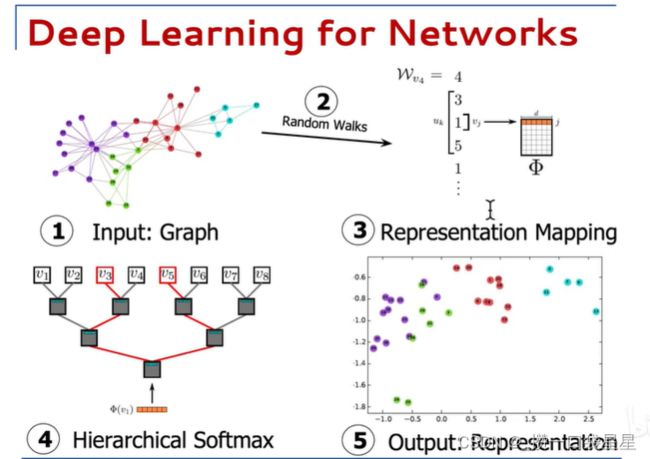
1.1.3 deepwalk
分为五个步骤
- 输入图
- 随机游走采样
- 图嵌入
- softmax（分类较多）
- 得到每个节点的向量表示
随机游走采样
计算条件概率
分层分类，每个节点是一个逻辑回归（工程应用）
参数优化有两次
1.1.4 评估
deepwalk在标注比例非常少的情况下表现非常好
可扩展，并行计算
1.1.5 展望
streaming:不需要知道图的全貌，可扩展
non-random walks:可以不随机，设置一些游走偏好优化随机游走的生成 ；把图当作语言，二者相辅相成
1.2 讨论
初级图机器学习算法
1.3 DeepWalk论文精读
DeepWalk: Online learning of social representation
用于图节点嵌入的在线机器学习算法
将图中节点编码为向量用于统计模型
1.3.1 Introduction
网络和图是比较稀疏的，如14亿人的社交网络，每个人只认识几百人，每个节点的连接是比较稀疏的。这种稀疏性使得一些离散算法（计算最短路径，计算传染病的传染过程等与路径相关的）的表现较好；而统计机器学习模型去进行分类或回归效果交叉，因为统计机器学习模型希望每个特征都有用，不希望很多特征都是0。
deepwalk学习到网络的连接结构信息，包含邻域信息和社群信息，表示为连续稠密低维向量。稠密指的是每一个元素都不为0。（14亿人的社交网络，每个节点的向量不是14亿维，而是十几维或者几十维，且每个元素不为0）
DeepWalk的输入是图，输出是每个节点的embedding。原图中相近的点，嵌入后向量是相似的。
异质图：节点和连接有多种类型
传统机器学习，数据集满足独立同分布（i.i.d.假设）；而图中节点之间有连接，不满足该假设。
Deepwalk是无监督学习，与节点标签无关。
该嵌入方法是通用的，几乎可以和任何统计算法结合。
文章贡献如下：
- 提出DEEPWALK算法，使用深度学习方法分析图，将每个节点编码为一个鲁棒的表示，利用随机游走学习图结构中的规则。
- 将文中方法应用于多标签的分类任务中，在稀疏问题上，有5%-10%的提升，在一些情况下可减少60%的训练数据。
- 文中展示了算法的可扩展性，可利用并行计算，应用于网络规模的图（如YouTube）。并通过较小的修改构建streaming版本（online learning）。
1.3.2 问题描述
设G = (V, E)，其中V是网络的节点，E表示连接关系的邻接矩阵，E ⊆ (V×V)。 给定部分标记的社交网络G[L] = (V, E, X, Y)，X表示特征，Y表示类别。每个节点都有S维特征，y表示标签集。
在传统的机器学习分类设置中，我们的目标是学习一个假设H，它将X的元素映射到标签集Y。在我们的例子中，我们可以利用G的结构中嵌入的节点的关联性的重要信息，来完成突出的表现。
在文献中，这被称为关系分类（或集体分类问题 ）。 传统的关系分类方法将问题作为无向马尔可夫网络中的推理，然后使用迭代近似推理算法（例如迭代分类算法 ，Gibbs 采样 或标签松弛 ）来计算给定网络结构的标签的后验分布。
不把标签和连接特征混合，仅在embedding中编码连接信息。
将节点本身的特征和反映连接信息的embedding用于机器学习分类
1.3.3 学习社会表示
我们希望学习具有以下特征的社会表示：
- 适应性：可适应网络的不断进化，而无需每次都从头训练。
- 社区意识：新表征的相似性应与网络中的相似性保持一致。
- 低维度：低维度的新表征，有更好的泛化性，训练和预测速度更快。防止过拟合
- 连续性：新表征中的特征是连续值，从而实现更强的健壮性。向量的细微差别对最终结果有影响，可以拟合出一个平滑的决策边界
随机游走
均匀随机游走，提取了图的部分信息，管中窥豹
在线增量学习
连接：幂律
选择在线随机游走作为捕获图形结构的基元，我们现在需要一种合适的方法来捕获这些信息。 如果连通图的度分布遵循幂律（如无标度网络），我们观察到顶点出现在随机游走中的频率也将遵循幂律分布。
二八定律、幂律分布、严重分布不均匀，少数中枢节点拥有极多连接
自然语言中的词频遵循类似的分布，并且来自语言建模的技术解释了这种分布行为。 为了强调这种相似性，我们在图 2 中展示了两种不同的幂律分布。第一种来自无标度图上的一系列短随机游走，第二种来自英文维基百科的 100,000 篇文章。
zipf定律：词频与词频排序名次的常数次幂成反比：只有少数的词被经常使用
语言模型
语言建模的目标是估计出现在语料库中的特定单词序列的可能性。
用前i-1个节点embedding预测第i个节点embedding
然而，随着游走长度的增加，计算这个条件概率变得不可行。
解决：用周围上下文预测缺失值（CBOW）或者skip-gram。 其次，上下文由出现在给定单词右侧和左侧的单词组成，无关顺序。 相反，该模型需要最大化任何单词出现在上下文中的概率，而不需要知道它与给定单词的偏移。
优化目标
好处：顺序独立很好地捕捉了随机游走提供的节点临近信息（随机游走生成的节点顺序没有意义）；模型较小，一次输入一个节点预测周围节点
该方法可以将节点编码为低维稠密连续的向量，包含节点的结构、连接和社群特征，虽然不包含类别信息，但可以用于预测类别信息。
1.3.4 算法
该算法由两个主要部分组成；首先是随机游走生成器，第二是更新过程。
伪代码
Algorithm 1 DeepWalk(G, w, d, γ, t)
-----------------------------------
Input: graph G(V, E)
window size w #左右窗口宽度
embedding size d #embedding的维度
walks per vertex γ #每个节点作为起始节点生成随机游走的次数
walk length t #随机游走的最大长度
Output: matrix of vertex representations Φ ∈ R^{|V|×d}
1: Initialization: Sample Φ from U[|V|×d] #随机初始化节点特征向量
2: Build a binary Tree T from V #softmax
3: for i = 0 to γ do #重复以下过程γ次
4: O = Shuffle(V) #随机打乱节点顺序
5: for each vi ∈ O do #遍历graph中的每个点
6: W[v[i]] = RandomWalk(G, v[i], t) #生成一个随机游走序列
7: SkipGram(Φ, W[v[i]], w) #由中心节点embedding预测周围节点，更新embeddng
8: end for
9: end for
SkipGram
Algorithm 2 SkipGram(Φ, W[v[i]], w)
-----------------------------------
1: for each v[j] ∈ W[v[i]] do #遍历当前随机游走序列里的每个节点
2: for each u[k] ∈ W[v[i]][j − w : j + w] do #遍历该节点周围窗口里的每个点
3: J(Φ) = − log Pr(u[k] | Φ(v[j])) #计算损失函数
4: Φ = Φ − α * ∂J / ∂Φ #梯度下降更新embedding矩阵
5: end for
6: end for
分层 Softmax
因为工程需要而进行的优化
当分类数较多时，采用分层softmax，将复杂度n将为logn（以2为底）
如：八分类问题转化为三个二分类逻辑回归问题
窗口宽度为1，节点1预测节点3和节点5，节点1通过查表得到一个d维向量，输入分层softmax,节点3和节点5都是标签，两条路径各自计算损失函数，各自优化更新。
优化
通过随机梯度下降进行优化
两套权重：N个节点的d维embedding和（N-1）个逻辑回归，每个有D个权重
N-1即非叶子节点的个数
随机梯度下降（SGD）用于优化这些参数。使用反向传播算法估计导数。 SGD 的学习率α在训练开始时初始设定为 2.5%，然后随着到目前为止看到的顶点数量而线性减小。
并行
多线程异步并行，加速训练，性能不变
社交网络的随机游走中的顶点的频率分布和语言中的单词都遵循幂律。这尝试产生了不常见顶点的长尾，因此，影响Φ的更新本质上将是稀疏的。这允许我们在多任务情况下使用异步版本的随机梯度下降（ASGD）。
1.3.5 算法变种
- streaming
在未知全图时，直接用采样出的随机游走训练embedding
将学习率α初始化为一个小的常数值。 这需要更长的时间来学习，但在某些应用中可能是值得的。
无需提前构建softmax树，来一个新的，就构建一个新的softmax叶节点 - 非随机游走
设置游走偏好
这种方法可以与streaming变体结合使用，在不需要明确构建整个图的情况下，在不断发展的网络上训练特征。
1.3.6 实验
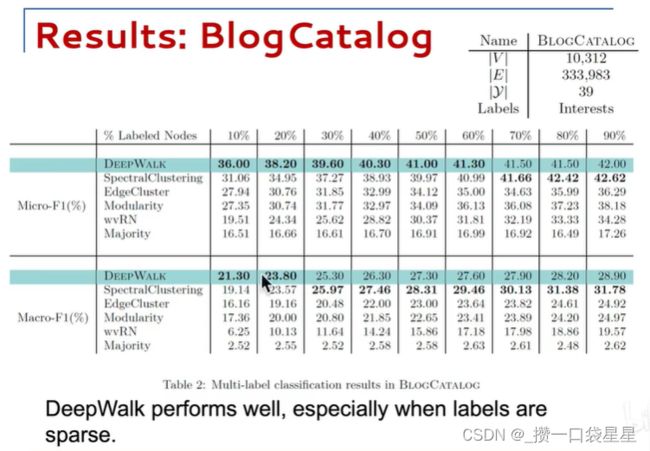
BlogCatalog：由博客作者相互关系构建的网络，标签是作者的主题类别。
FLICKR：图片共享网站用户之间的联系人网络，标签是用户感兴趣的组。
YOUTUBE：视频用户关系网络，标签是喜欢同一视频风格的群体。
macro-f1:将每一类的f1取平均
micro-f1:用总体的TP/FN/FP/TN计算f1
分别使用训练集的10%-90%进行训练，可以看到DEEPWALK优于频聚类以外的其它方法，当标注少时，DEEPWALK比频聚类更有优势，这是文中算法的特点。
实验分别标注了1%-10%的数据，可以看到DEEPWALK优于其它算法，它只需要60%甚至更少的数据，就能达到与其它算法相同的精度。
YOUTUBE网络比其它网络大得多，频聚类和模矩阵无法满足这样的计算量。这种网络也更接近现实世界。使用1%-10%比例标注。
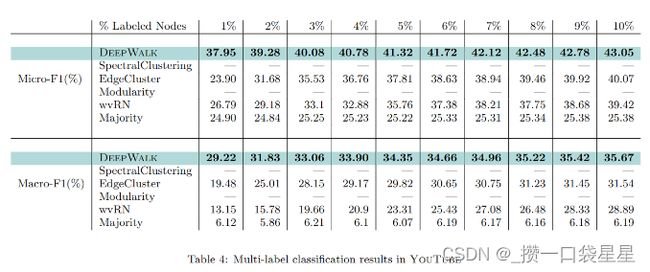
参数对分类任务模型的影响
语言模型是对不可见的隐式graph建模，可见graph的分析方法可以促进非可见graph的研究
2 Node2Vec
对DeepWalk进行改进，有偏随机游走
调节权重指定搜索倾向
若p值较小，更易徘徊，广度，是一个微观视角
若q值较小，更易去远的地方，深度，宏观视角
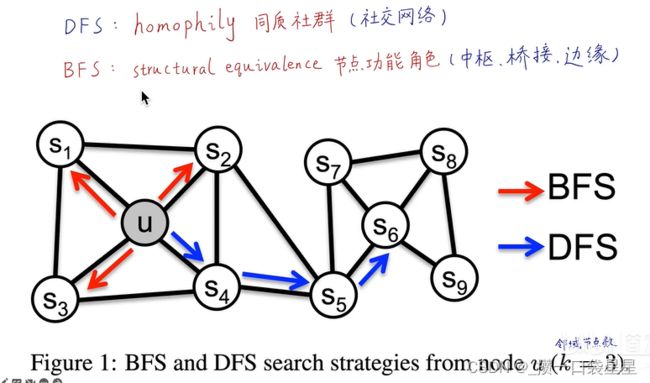
deepwalk属于一阶采样，下一节点位置只取决于当前的节点位置
node2vec属于二阶采样，下一节点位置与当前的节点位置和上一节点位置有关
2.1 讨论
阿里巴巴电商推荐
2.2 论文精读
node2vec: Scalable feature learning for networks
可扩展的图嵌入表示学习算法
node2vec 可以学习根据节点的网络角色或它们所属的社区组织节点的表示。 通过开发一系列有偏随机游走来实现这一点，它可以有效地探索给定节点的不同邻域。
贡献如下：
1.提出了 node2vec，这是一种用于网络中特征学习的高效可扩展算法，可使用 SGD 有效优化新的网络感知、邻域保留目标。
2.算法的灵活性，下游任务表现好，所提取的特征包含了丰富的语义信息
3.从节点嵌入扩展到了连接嵌入，进而可以解决连接预测问题
4.应用于现实网络中进行多标签分类和链路预测
论文数据集：http://snap.stanford.edu/node2vec
无监督特征学习方法通常利用图的各种矩阵表示的光谱特性，特别是拉普拉斯矩阵和邻接矩阵
在线性代数的视角下，这些方法可以被视为降维技术:线性(如PCA)和非线性(如IsoMap)
缺点：
- 矩阵分解开销很大
- 很难应用到大型网络
- 对于不同网络中的优化目标不具有鲁棒性（如同质性和结构等效性）
- 一般会对底层网络结构和预测任务之间的关系进行假设，造成不能在不同的网络上有效地泛化
节点可能的采样策略很多，导致学习到的特征表示不同。
之前的工作的主要缺点：
没有一个明确的良好的采样策略可以适用于所有的网络、预测任务
不能提供从网络中采样节点的灵活性（采样策略不灵活）
引出node2vecv的优点：
通过设计一个不受特定采样策略约束的灵活目标，并提供参数来调整已探索的搜索空间
基于监督学习的图嵌入：用节点标签做图嵌入，使其适应于下游的任务。不科学，只能解决和标签相关的下游任务
2.2.1 特征学习框架
优化目标
两个假设：周围节点互不影响，两个节点之间相互影响的程度一样
2.2.2 算法
随机游走
最简单的有偏随机游走
与纯BFS/DFS方法相比，随机游走的一些好处：就空间和时间要求而言，随机游走在计算上是高效的
2.2.3 伪代码
在任意随机游走中，由于起始节点u的选择，会存在一种隐式偏差。
我们通过学习所有节点的表示，对每个节点模拟r rr个固定长度l ll的随机游走来抵消这种偏差
2.2.4 node embedding 扩展到link embedding
得到节点的嵌入后，通过一步运算得到两节点之间连接的嵌入表示
