线段树SegmentTree
什么是线段树,它能解决什么样的问题?
仰望天空,妳我亦是行人.✨
个人主页——微风撞见云的博客
数据结构与算法专栏的文章图文并茂生动形象简单易学!欢迎大家来踩踩~
希望本文能够给读者带来一定的帮助文章粗浅,敬请批评指正!
文章目录
- 问题引入
- 线段树的概念
- Query
- Update
- 代码实现 —— Build
- 代码实现 —— Update
- 代码实现 —— Query
- 整体代码
- 结语
问题引入
假设我们现在有一个非常大的数组,而对于数组里面的数字我们要反反复复不断地做两个操作:
- 不断地
随机选定一块区间,求出这块区间里面的所有数字的和。我们暂且称之为query。 - 不断地
修改这个数组中的某个元素的值,即array[i] = num 。我们暂且称之为update。
好的,那么现在我们来看看上面的①、②操作时间复杂度分别为多少:
情况一(可以保证update是高效的):
- 对query来说,假如区间范围为L~R ,如果用从左到右依次累加的话,那么query(L,R)的时间复杂度为
O(n); - 而对于update来说,只需要将指定的下标元素修改掉就可以了,所以update(Index,value)的时间复杂度为
O(1);
情况二(可以保证query是高效的):
- 对query来说,我们用一个一维的前缀和pre[]来预处理一下,那么query(L,R)的操作就可以简化为pre[R] - pre[L],时间复杂度为
O(1); - 可是这样的操作之后,对于update来说,我们在修改完指定的下标元素后又需要维护我们的前缀和数组pre[],而维护操作的时间复杂度为O(n),所以update(Index,value)的时间复杂度从O(1)变为 了
O(n);
我们会发现,不论如何改变,query和update都无法同时达到O(1)的时间复杂度,总是在O(1)和O(n)之间反复横跳。那么当我们频繁的调用这两个方法时,算法的总体速度都不会特别快。对于这种在线的区间操作,我们有没有什么更好的办法呢?答案当然是有的,也就是用到了咱们的线段树——SegmentTree,它可以把两者的时间复杂度稍微平均一下,使得总体的时间复杂度降为O(log n),让我们一起来看看,线段树究竟是什么,又该如何实现并使用它吧!
线段树的概念
线段树是一种特殊的二叉树,它是一种数据结构,更是一种工具。它能把在线的区间修改、维护,从O(N)的时间复杂度变成O(log n)。
Query
我们还是用刚才的arr数组作为原数组,下标从0开始,数值分别为0,1,3,5,7,9,11。

我们如何将这个数组变为线段树呢?
首先我们需要知道线段树的结构,它的每一个结点存储的是一段区间值的总和。根节点存放所有元素的和,然后我们把区间劈成两半,(int)(0 +(5 - 0) / 2) = 2,那么左边为[0,2] 右边为 [3,5]。

下面的以此类推,直到范围不再是一个区间,而是具体的数值,那么我们就不再对它进行分解了(也没办法再分了对吧),构造出来线段树就如图所示:

然后我们说它是一棵线段树对吧,那么它就应该具有线段树的特点,每个结点储存的值应该是区间的总和,那么我们将数值给他从叶子结点往上给它填充起来。

那线段树我们就算是构造出来了,但是这么做有什么好处呢?
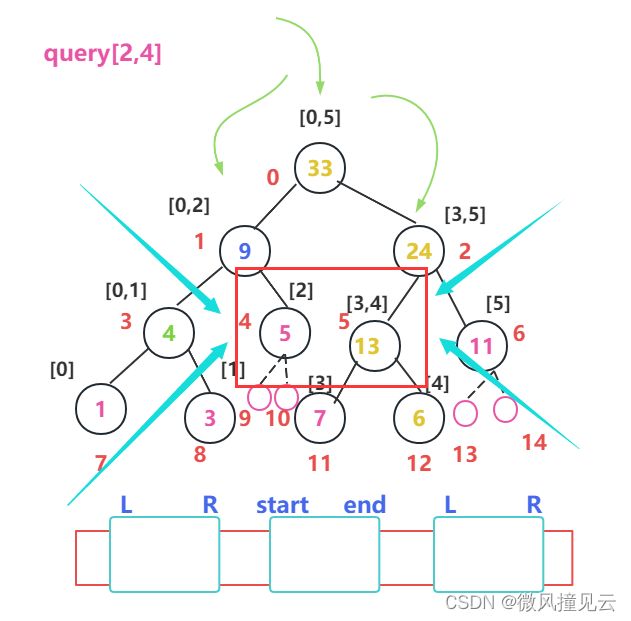
假设我们要计算的是这些数字的和:
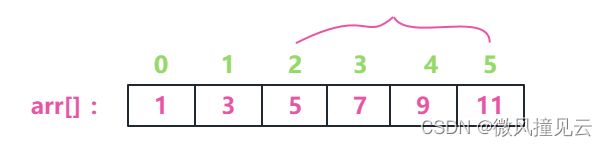
那么我们可以先把[2,5]这个范围转移到线段树里面,从根节点做搜索:

但是我们会发现根节点并不是[2,5],那么我们就可以将[2,5]劈成两半:[2]和[3,5],左边的往左子树找,右边的往右子树找:

我们可以发现[3,5]是可以在右子树上直接找到的,那么我们就不必再继续“砍”它了;而[2]需要寻找两次,然后找到对应的值:

那么最后[2,5]的和就应该是[2] + [3,5] = 5 + 27 = 32,那么时间复杂度也从O(n) 降到了O(log n)。
Update
query是知道了,那么update又该怎么做呢?
假如我们现在想把arr[4] 的值改为6,那么我们只需要顺藤摸瓜,找到叶子结点为4的这个元素,然后顺着父节点一路改回去,直到改掉根节点(感觉特像回溯有没有!好吧,其实就是回溯,嘿嘿O(∩_∩)O ~),由于我们修改的时候,其他路径的结点没有受到任何的影响,所以我们此处update的时间复杂度依旧为O(log n)。(左下角的结点值是1,我给写漏了,在后面的图中补上了)
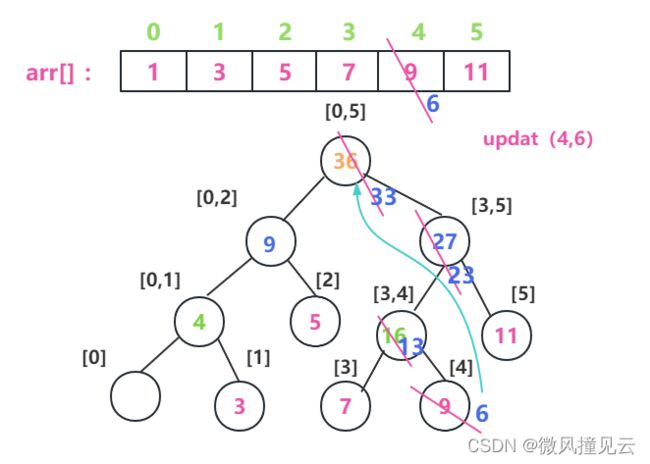
那么下面我们就来想想如何用代码来实现 biuld 以及 query 和 update操作。
代码实现 —— Build
首先我们需要思考应该怎样来保存这棵树?根据观察,我们可以发现,这样的树并非一棵完全二叉树,那么我们能不能够给它插两个枝干让它变为完全二叉树呢?当然可以!

这几个叶子结点也太小了,哈哈哈,大家别介意啊。我们加入了两个叶子结点,保证这个树能够构造为完全二叉树,这样的话,咱们就可以去思考,该如何保存这棵完全二叉树。
经思考,我们可以用数组来保存这棵树的每个结点,根据我们构造的树来填充一下数组tree[],填完tree[]之后,图片如下↓
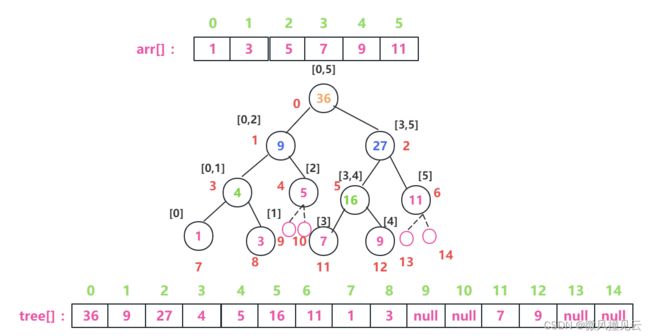
对于一棵完全二叉树而言,我们应该知道几个基本知识点:
- 假设某个结点的下标为
index,那它的左子结点的下标应该为2 * index + 1,右子结点的下标为2 * index + 2,现在我们给这个树的结点加上标记,一共是2的4次方(树的高度)减一个 = 15个结点。
## 为什么可以确定数的结点为15个?树的高度又该如何计算?
> 树的高度其实是根据节点的个数来确定的,比如这道题里面一共有6的结点,我们要对它进行倍增的拆分,
> 由于倍增是根据2的指数次方来倍增的,所以我们同样应该以2分的方式对数组进行拆分,
> 拆分为[0,2]--[3,5] ,然后是[0,1]--[1,2] , [3,4]--[4,5],最后就是把每个分组拆分为单个数字,即为最后一层
> 所以,数的高度理论上应该为1(根节点)+ log以2为底 6的对数(向下取整)+1(单个数字) --> 4;
> 由完全二叉树的性质可知,一个高度为h的完全二叉树,子节点个数为2的h次方-1,即2的4次方-1 --> 15;
> <p>
> 在完全二叉树中:
> 左结点的下标 == 父节点下标 * 2 + 1;
> 右结点的下标 == 父节点下标 * 2 + 2;
我们该如何来构建这颗树呢?为了方便区分,我们对与树有关的变量加个后缀比如left_node,而与原数组有关的变量则不带有该后缀,例如start、end、L、R。
建立树的步骤:
-
开一个有一定容量的数组,容量大小可以自己根据完全二叉树的特点稍作计算得出。
-
编写一个方法:
build_tree(int[] arr, int[] tree, int node, int start, int end) -
参数分别代表
arr: 原数组;tree : 线段树;node : 根节点;start : 根节点的左边界;end : 根节点的右边界 -
思路是这样的:我们
从根节点出发,使用递归函数进行对二叉树的创建。既然是递归,那就应该有递归出口和递归体。 -
递归出口:
当左边界start == 右边界end的时候,说明该叶子结点已经构建好了,此时我们只需要将数组中的值赋给这个叶子结点。 -
递归体:我们
先找出左孩子和右孩子,接着还是对区间进行“劈砍”的操作,以便确定构建左右子树时候的边界。最后记得将回溯一下——将左右孩子的值相加赋值给父节点。
Java代码如下:
/**
* @param arr: 原数组
* @param tree : 线段树
* @param node : 根节点
* @param start : 根节点的左边界
* @param end : 根节点的右边界
*/
static void build_tree(int[] arr, int[] tree, int node, int start, int end) {
if (start == end) {
tree[node] = arr[start];
} else {
int mid = (start + end) / 2;
int left_node = 2 * node + 1;
int right_node = 2 * node + 2;
build_tree(arr, tree, left_node, start, mid);
build_tree(arr, tree, right_node, mid + 1, end);
tree[node] = tree[left_node] + tree[right_node];
}
}
测试:
public static void main(String[] args) {
arr = new int[]{1, 3, 5, 7, 9, 11};
int size = arr.length;
tree = new int[size * 4];
build_tree(arr, tree, 0, 0, size - 1);
//查看构建的树
for (int i = 0; i < 15; i++) {
System.out.printf("tree[%d] = %d\n", i, tree[i]);
}
}
/**测试结果如下:
tree[0] = 36
tree[1] = 9
tree[2] = 27
tree[3] = 4
tree[4] = 5
tree[5] = 16
tree[6] = 11
tree[7] = 1
tree[8] = 3
tree[9] = 0
tree[10] = 0
tree[11] = 7
tree[12] = 9
tree[13] = 0
tree[14] = 0
*/
代码实现 —— Update
- 接下来我们来实现修改操作
update_tree(int[] arr, int[] tree, int node, int start, int end, int idx, int val)
更新的步骤:
-
同样需要
刚才的参数,新的参数idx 也就是目标结点的下标,val 是修改后的值。 -
参数分别代表
arr: 原数组;tree : 线段树;node : 根节点;start : 根节点的左边界;end : 根节点的右边界,idx : 目标结点的下标,val : 修改后的值。 -
同样使用
递归来实现:- 递归出口:
start == end,达到条件后,说明找到idx的结点,修改数组和树里面idx下标元素的值。 - 递归体:
二分的思想,同样先砍一刀,如果当前的idx在左半边,则向左子树递归,右子树同理;同样记得在回溯的时候把左右孩子结点加起来的值赋值给父节点完成更新。
- 递归出口:
-
举个例子:将arr[4]的值改为6,
黄色字体为修改后的值。和下面的测试代码对照之后,可以证明我们的操作是正确的。
/**
* @param arr: 原数组
* @param tree : 线段树
* @param node : 根节点
* @param start : 查找范围的左边界
* @param end : 查找范围的右边界
* @param idx : 目标结点的下标
* @param val : 修改后的值
*/
static void update_tree(int[] arr, int[] tree, int node, int start, int end, int idx, int val) {
if (start == end) {
arr[idx] = val;
tree[node] = val;
} else {
int mid = (start + end) / 2;
int left_node = 2 * node + 1;
int right_node = 2 * node + 2;
if (idx >= start && idx <= mid) {
update_tree(arr, tree, left_node, start, mid, idx, val);
} else {
update_tree(arr, tree, right_node, mid + 1, end, idx, val);
}
tree[node] = tree[left_node] + tree[right_node];
}
}
测试:
public static void main(String[] args) {
arr = new int[]{1, 3, 5, 7, 9, 11};
int size = arr.length;
tree = new int[size * 4];
build_tree(arr, tree, 0, 0, size - 1);
/*//查看构建的树
for (int i = 0; i < 15; i++) {
System.out.printf("tree[%d] = %d\n", i, tree[i]);
}
System.out.println();*/
//将arr[4]的值改为6
update_tree(arr, tree, 0, 0, size - 1, 4, 6);
for (int i = 0; i < 15; i++) {
System.out.printf("tree[%d] = %d\n", i, tree[i]);
}
System.out.println();
}
/**
tree[0] = 33
tree[1] = 9
tree[2] = 24
tree[3] = 4
tree[4] = 5
tree[5] = 13
tree[6] = 11
tree[7] = 1
tree[8] = 3
tree[9] = 0
tree[10] = 0
tree[11] = 7
tree[12] = 6
tree[13] = 0
tree[14] = 0
*/
代码实现 —— Query
接下来我们来实现查询操作query_tree(int[] tree, int node, int start, int end, int L, int R)
-
参数分别代表
arr: 原数组;tree : 线段树;node : 根节点;start : 根节点的左边界;end : 根节点的右边界,L : 查询框定的左边界,R : 查询框定的右边界。 -
查询的步骤同样使用递归来实现:
举个例子:查询[2,5]这个范围所有数的和。
我们从根节点出发,那么[2,5]是在根节点的范围[0,5]之内的,我们还是劈成两半分开找

递归出口:
- 当我们
砍成两半开始递归的时候,我们会发现一种情况,我们左子树结点的范围有可能根本就不在我们要找的范围[L,R]里面,这个时候我们就return掉。那什么情况会不在范围内呢?第一种就如下图所示,R在start的左边,或者L在end右边。
if (R < start || L > end) return 0;
- 另外一种情况就是
在那个区间内,这里请大家思考一个问题,我们是选择和之前一样(start==end结束然后返回结点值)呢?还是说我们的区间在大区间内部就返回结点值?答案显然是后者!为什么呢?因为如果是第一种情况,我们每次都需要直接搜到底再回溯上来,这样很低效,因为线段树的每个结点都记录了对应区间的总和,那么我们直接返回这个区间总和就行,相当于剪枝了。
Java代码如下:
/**
* @param tree : 线段树
* @param node : 根节点
* @param start : 查找范围的左边界
* @param end : 查找范围的右边界
* @param L : 查询框定的左边界
* @param R : 查询框定的右边界
*/
static int query_tree(int[] tree, int node, int start, int end, int L, int R) {
/*System.out.printf("start = %d\n", start);
System.out.printf("end = %d\n", end);
System.out.println();*/
if (R < start || L > end) {
return 0;
} else if (L <= start && end <= R) {
return tree[node];
} else {
int mid = (start + end) / 2;
int left_node = 2 * node + 1;
int right_node = 2 * node + 2;
int sum_left = query_tree(tree, left_node, start, mid, L, R);
int sum_right = query_tree(tree, right_node, mid + 1, end, L, R);
return sum_left + sum_right;
}
}
public static void main(String[] args) {
arr = new int[]{1, 3, 5, 7, 9, 11};
int size = arr.length;
tree = new int[size * 4];
build_tree(arr, tree, 0, 0, size - 1);
/*//查看构建的树
for (int i = 0; i < 15; i++) {
System.out.printf("tree[%d] = %d\n", i, tree[i]);
}
System.out.println();*/
//将arr[4]的值改为6
update_tree(arr, tree, 0, 0, size - 1, 4, 6);
for (int i = 0; i < 15; i++) {
System.out.printf("tree[%d] = %d\n", i, tree[i]);
}
System.out.println();
//计算[2,5]区间类所有数字加起来等于多少
int s = query_tree(tree, 0, 0, size - 1, 2, 4);
System.out.println("s = " + s);
}
/**
s = 18
*/
可以看到,5 + 13 =18,结果正确。
整体代码
/**
* @Auther: LiangXinRui
* @Date: 2023/3/1 17:13
* @Description: 查询指定区间内, 所有数的和(可修改). RMQ by SegmentTree
*/
public class SegmentTree {
static int[] arr;
static int[] tree;
/**
* @param arr: 原数组
* @param tree : 线段树
* @param node : 根节点
* @param start : 根节点的左边界
* @param end : 根节点的右边界
*/
static void build_tree(int[] arr, int[] tree, int node, int start, int end) {
if (start == end) {
tree[node] = arr[start];
} else {
int mid = (start + end) / 2;
int left_node = 2 * node + 1;
int right_node = 2 * node + 2;
build_tree(arr, tree, left_node, start, mid);
build_tree(arr, tree, right_node, mid + 1, end);
tree[node] = tree[left_node] + tree[right_node];
}
}
/**
* @param arr: 原数组
* @param tree : 线段树
* @param node : 根节点
* @param start : 查找范围的左边界
* @param end : 查找范围的右边界
* @param idx : 目标结点的下标
* @param val : 修改后的值
*/
static void update_tree(int[] arr, int[] tree, int node, int start, int end, int idx, int val) {
if (start == end) {
arr[idx] = val;
tree[node] = val;
} else {
int mid = (start + end) / 2;
int left_node = 2 * node + 1;
int right_node = 2 * node + 2;
if (idx >= start && idx <= mid) {
update_tree(arr, tree, left_node, start, mid, idx, val);
} else {
update_tree(arr, tree, right_node, mid + 1, end, idx, val);
}
tree[node] = tree[left_node] + tree[right_node];
}
}
/**
* @param tree : 线段树
* @param node : 根节点
* @param start : 查找范围的左边界
* @param end : 查找范围的右边界
* @param L : 查询框定的左边界
* @param R : 查询框定的右边界
*/
static int query_tree(int[] tree, int node, int start, int end, int L, int R) {
/*System.out.printf("start = %d\n", start);
System.out.printf("end = %d\n", end);
System.out.println();*/
if (R < start || L > end) {
return 0;
} else if (L <= start && end <= R) {
return tree[node];
} else {
int mid = (start + end) / 2;
int left_node = 2 * node + 1;
int right_node = 2 * node + 2;
int sum_left = query_tree(tree, left_node, start, mid, L, R);
int sum_right = query_tree(tree, right_node, mid + 1, end, L, R);
return sum_left + sum_right;
}
}
//Finish:Tree's build、update、query test.
public static void main(String[] args) {
arr = new int[]{1, 3, 5, 7, 9, 11};
int size = arr.length;
tree = new int[size * 4];
build_tree(arr, tree, 0, 0, size - 1);
//查看构建的树
for (int i = 0; i < 15; i++) {
System.out.printf("tree[%d] = %d\n", i, tree[i]);
}
System.out.println();
//将arr[4]的值改为6
update_tree(arr, tree, 0, 0, size - 1, 4, 6);
for (int i = 0; i < 15; i++) {
System.out.printf("tree[%d] = %d\n", i, tree[i]);
}
System.out.println();
//计算[2,5]区间类所有数字加起来等于多少
int s = query_tree(tree, 0, 0, size - 1, 2, 4);
System.out.println("s = " + s);
}
}
到此,线段树的简单应用就结束了,你学会了吗?码字实属不易,如果有帮助就点个赞吧~
完结撒花ヽ(°▽°)ノ
结语
初学一门技术时,总有些许的疑惑,别怕,它们是我们学习路上的点点繁星,帮助我们不断成长。
文章粗浅,希望对大家有帮助!
参考B栈大佬“正月点灯笼”的视频:【数据结构】线段树(Segment Tree)