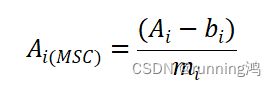高光谱预处理方法之MSC与SNV——matlab实现

     光谱多元散射校正（MSC）的目的：经过散射校正后得到的光谱数据可以有效的消除由于散射水平不同带来的光谱差异，从而增强光谱与数据之间的相关性。

（1）求得所有光谱数据的平均值作为“理想光谱”；

  计算平均光谱：

（2）将每个样品的光谱与平均光谱进行一元线性回归运算，求得各光谱相对于标准光谱的线性平移量(回归常数)和倾斜偏移量(回归系数)，

  一元线性回归：

mi和bi分别表示各样品近红外光谱Ai与平均光谱A进行一元线性回归后得到的相对偏移系数和平移量

（3）在每个样品原始光谱中减去线性平移量同时除以回归系数修正光谱的基线相对倾斜，这样每个光谱的基线平移和偏移都在标准光谱的参考下予以修正，而和样品成分含量所对应的光谱吸收信息在数据处理的全过程中没有任何影响，所以提高了光谱的信噪比。

  多元散射校正：

     缺点：首先要求建立一个待测样品的“理想光谱”，但在实际应用中，“理想光谱”是很难得到的，但通由取所有光谱的平均光谱作为一个理想的标准光谱，用来修正各样品近红外光谱间的相对基线平移和偏移现象，是完全可以的。

 

      与MSC类似，变量标准化(standard normalized variate,SNV)也可以用来校正样品间因散射而引起的光谱误差。但两者的算法有所不同。

    SNV是原光谱减去该光谱的平均值μ后，再除以数据的标准偏差σ（标度化），实质是使原来的光谱数据标准正态化。

=−Z_i=(x_i-μ)/σ

     变量标准化的光谱数据均值为0，标准差为1。由于SNV是对每条光谱单独进行校正，因此一般认为它的校正能力比MSC要稍微强点，尤其是样品组之间差异较大的时候。

 Matlab实现MSC代码：

data = xlsread('C:\Users\HASEE\Desktop\练习数据.xlsx') ;
 Xnir = data(2:end,1:end) ;
[me, ] = mean(Xnir);
[m, n] = size(Xnir);
for i = 1:m    
  p = polyfit(me, Xnir(i,:),1);    
  Xmsc(i,:) = (Xnir(i,:) - p(2) * ones(1, n))./(p(1) * ones(1, n));
end

subplot(2,2,1)
plot(data(1:1,:),Xnir);
title("数据集的原始光谱图")
axis([935.0 1635.0,-inf,inf])
subplot(2,2,2)
plot(data(1:1,:),Xmsc);
title("经过MSC处理后的光谱图")
axis([935.0 1635.0,-inf,inf])

  Matlab实现SNV代码：

data = xlsread('C:\Users\HASEE\Desktop\练习数据.xlsx') ;
 Xnir = data(2:end,1:end) ;
[me, ] = mean(Xnir);
[m, n] = size(Xnir); % Xnir 为输入光谱数据，行为样本，列为波长点
Xm = mean(Xnir, 2);  % 求均值，注意是对行求均值，
dX = Xnir - repmat(Xm, 1, n); 
Xsnv = dX./ repmat(sqrt(sum(dX.^2,2)/n), 1, n) ; 

subplot(2,2,3)
plot(data(1:1,:),Xnir);
title("数据集的原始光谱图")
axis([935.0 1635.0,-inf,inf])
subplot(2,2,4)
plot(data(1:1,:),Xsnv);
title("经过SNV处理后的光谱图")
axis([935.0 1635.0,-inf,inf])

 效果图