leetcode：222. 完全二叉树的节点个数、669. 修剪二叉搜索树、513. 找树左下角的值（JavaScript）

222. 完全二叉树的节点个数

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

示例 1：

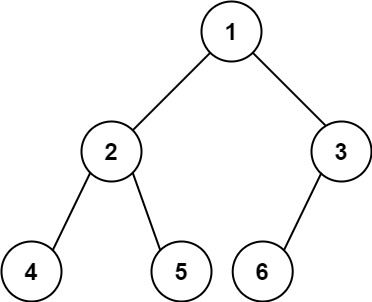
输入：root = [1,2,3,4,5,6]
输出：6

示例 2：

输入：root = []
输出：0

示例 3：

输入：root = [1]
输出：1

提示：

• 树中节点的数目范围是[0, 5 * 104]
• 0 <= Node.val <= 5 * 104
• 题目数据保证输入的树是 完全二叉树

迭代：层序遍历，统计每层节点数量，累加。

var countNodes = function(root) {
    let count = 0;
    if (!root) return 0;
    const que = [root];
    // 遍历每层元素
    while (que.length) {
        let len = que.length;
        // 统计节点个数
        count += len;
        // 记录每层元素的子元素
        while (len) {
            const tem = que.shift();
            tem.left && que.push(tem.left);
            tem.right && que.push(tem.right);
            len--;
        }
    }
    return count;
};

递归

var countNodes = function(root) {
    if (!root) return 0;
    // 统计左子树节点数量
    const leftDeep = countNodes(root.left);
    // 统计右子树节点数量
    const rightDeep = countNodes(root.right);
    // 将深度返回给当前元素的父元素
    return leftDeep + rightDeep + 1;
};

669. 修剪二叉搜索树

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。 可以证明，存在 唯一的答案 。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

示例 1：

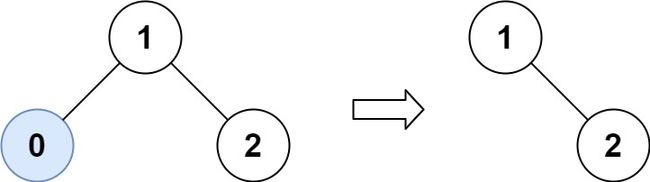
输入：root = [1,0,2], low = 1, high = 2
输出：[1,null,2]

示例 2：

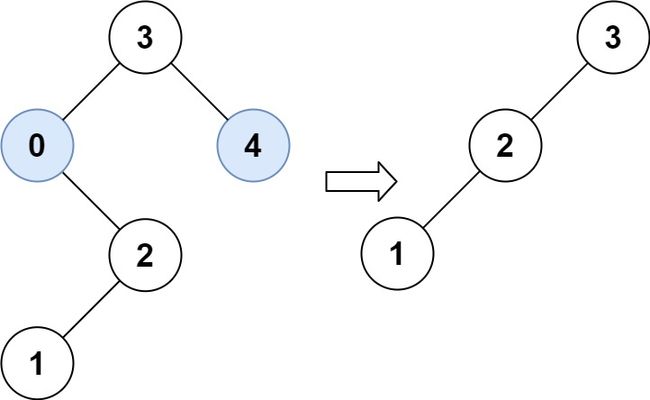
输入：root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出：[3,2,null,1]

提示：

• 树中节点数在范围 [1, 104] 内
• 0 <= Node.val <= 104
• 树中每个节点的值都是 唯一 的
• 题目数据保证输入是一棵有效的二叉搜索树
• 0 <= low <= high <= 104

思路：

本题采用递归前序遍历，在递归遍历的过程中，如果当前节点的值小于最小边界，那么就在当前节点的右子树中寻找第一个满足条件的结点返回（因为右子树的节点值一定大于当前节点的值），如果如果当前节点的值小于最小边界，那么就在当前节点的右子树中寻找第一个满足条件的结点返回。

var trimBST = function(root, low, high) {
    if (!root) return null;
    if (root.val < low) {
        // 递归查找右子树
        return trimBST (root.right, low, high);
    } 
    if (root && root.val > high) {
        // 递归查找左子树
        return trimBST (root.left, low, high);
    }
    // 递归遍历
    root.left = trimBST (root.left, low, high);
    root.right = trimBST (root.right, low, high);
    return root;
};

513. 找树左下角的值

难度中等265收藏分享切换为英文接收动态反馈

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层 最左边 节点的值。

假设二叉树中至少有一个节点。

示例 1:

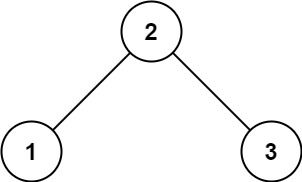
输入: root = [2,1,3]
输出: 1

示例 2:

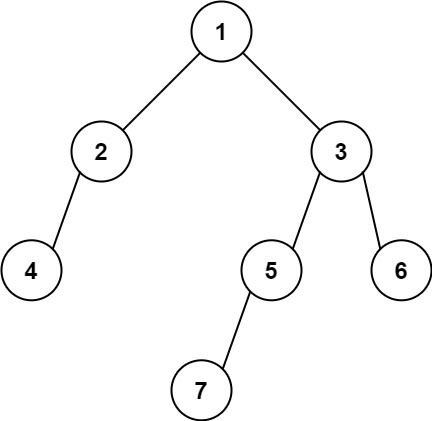
输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7

提示:

• 二叉树的节点个数的范围是 [1,104]
• -231 <= Node.val <= 231 - 1

思路：

这一题就不适合用递归来做，递归一来不好判断是否是深度最大的叶子结点，而来也不好判断是否是最左边的叶子结点。但是用层序遍历很容易判断。

最左边的节点

记录每一层的第一个元素，因为我们层序遍历是从左向右扫描每一层节点，所以每一层第一个元素就是该层最左边的结点。

res = que[0].val;

最底层的结点

因为记录了每一层的最左边节点，所以最后一层的目标节点一定会是循环结束前最后一个记录的值。

var findBottomLeftValue = function(root) {
    if (!root) return root.val;
    let res;
    const que = [root];
    // 遍历每一层
    while (que.length) {
        let len = que.length;
        // 标记每一层的第一个元素
        res = que[0].val;
        while (len--) {
            // 记录每一层元素的孩子结点
            root = que.shift();
            // 若孩子存在就进入队列
            root.left && que.push(root.left);
            root.right && que.push(root.right);
        }
    }
    return res;
};