蓝桥杯刷题007——七段码
七段码
七段码2020年第十一届蓝桥杯省赛，填空题，lanqiao0J题号595
【问题描述】
七段数码管，一共有7个发光二极管，问能表示多少种不同的字符，要求发光的二极管是相连的。
七段数码管，一共有7个管，所以总共有
种情况。
【解题思路】
【手算】
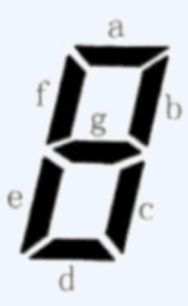
因为图形简单，出现的情况并不多，直接手算也行，约5~10分钟。用字符表示数码管不太方便，改用数字: a ~ g分别用1~7表示。统计亮1,2,3,4,5,6,7个灯分别有多少种情况。
【编码】
这道题需要用到“联通矩阵”+“DFS(深度优先搜索)” 。
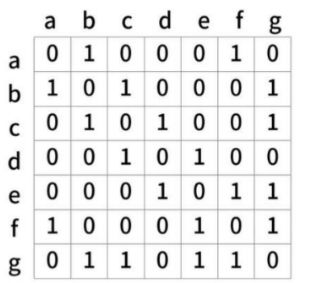
首先介绍一下联通矩阵 ，以上图为例，a只与b，f连通，所以a行的b，f列为1，其余列为0。b与a，c，g连通，所以b行的a，c，g列为1，其余列为0。以此类推，可以得到如下的矩阵。
连通矩阵
然后深度优先搜索 （DFS）大家可以参考一下这篇文章：DFS初入门(深度优先搜索)(Python)
- 七个灯总共有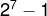种方案。 所以循环127次，对每次循环进行判断即可。
- 第i个方案用choose来选择点亮的灯：将 i 转换成二进制的choose，1代表亮，0代表不亮。
- 因为是灯是连通的所以从任意一点都可以走到其他点 ，所以找该方案第一个亮的灯，让它去做一个深度优先搜索就可以了。
- 深度优先搜索：从第一个亮的灯沿着选择的和可到达的（连通且未到达）点走一圈。
- 对深度优先搜索结果进行判断，排除方案选择了但走一圈却到不了的情况，留下方案选择了且走到了的情况。统计这种情况数得到答案。
【题解】
【手算】
这些组合中的连续亮灯，分7种情况统计:
- 亮一个灯:1、2、3、4、5、6、7，共7种
- 亮两个灯:12、13、24、25、34、36、45、46、57、67，共10种
- 亮三个灯:123、124、125、134、136、234、245、246、257、345、346、367、456、457、467、567，共16种
- 亮四个灯，这时不要直接数四个灯，情况与灭三个灯是等价的，数三个灯比数四个灯简单。注意灭三个灯后其他的四个亮灯是连续的:灭123、124、125、126、127、134、135、136、137、157、167、245、257、267、346、357、367、457、467、567，共20种
- 亮五个灯:数灭两个灯的情况:灭12、灭13、灭14、...等，共19种
- 亮六个灯:数灭一个灯的情况，有7种
- 亮七个灯:有1种。
- 对以上所有情况求和，答案是80。、
【编码】
Edge = [ # 七段码的连通矩阵
[0, 1, 0, 0, 0, 1, 0],
[1, 0, 1, 0, 0, 0, 1],
[0, 1, 0, 1, 0, 0, 1],
[0, 0, 1, 0, 1, 0, 0],
[0, 0, 0, 1, 0, 1, 1],
[1, 0, 0, 0, 1, 0, 1],
[0, 1, 1, 0, 1, 1, 0]]
def dfs(k):
for i in range(7):
if Edge[k][i] and choose[i] and not visited[i]: # 连通+亮+没访问过
visited[i] = 1 # 访问了，标记为已访问
dfs(i) # 在走过的点继续走下一个
ans = 0
for i in range(1, 128): # 2^7-1=127种方案
choose = [0 for _ in range(7)] # 选择那些灯灯亮或者不亮
visited = [0 for _ in range(7)]
# 十进制(第i个方案)--》二进制choose
x = i
j = 0
while x:
if x % 2:
choose[j] = 1
x //= 2
j += 1
k = 0
# 找该方案第一个亮的灯（因为是连通的所以从任意一点都可以走到其他点）
while not choose[k]:
k += 1
visited[k] = 1 # 访问了，标记为已访问
dfs(k)
flag = True
for j in range(7):
if choose[j] and not visited[j]:# 方案选择了，但走一圈却到不了
flag = False # 这个情况不满足
break
if flag: # 方案选择了却走到了
ans += 1
print(ans) # 80