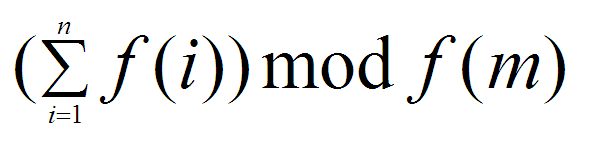蓝桥杯刷题记录--第三周
一.斐波那契
斐波那契数列大家都非常熟悉。它的定义是:
f(x) = 1 .... (x=1,2)
f(x) = f(x-1) + f(x-2) .... (x> 2)
对于给定的整数 n 和 m,我们希望求出:
f(1) + f(2) + ... + f(n) 的值。但这个值可能非常大,所以我们把它对 f(m) 取模。
公式如下
但这个数字依然很大,所以需要再对 p 求模。
思路:使用矩阵快速幂求解
n,m,p=map(eval,input().split())
def mul(a,b):
i=len(a)
global p
j=len(b[0])
ans=[[0 for _ in range(j) ] for __ in range(i)]
for ii in range(i):
for jj in range(j):
for k in range(len(a[0])):
ans[ii][jj]+=(a[ii][k]*b[k][jj])%p
ans[ii][jj]%=p
return ans
def mul1(a,b):
i=len(a)
global p
j=len(b[0])
ans=[[0 for _ in range(j) ] for __ in range(i)]
for ii in range(i):
for jj in range(j):
for k in range(len(a[0])):
ans[ii][jj]+=(a[ii][k]*b[k][jj])
return ans
def quickn(num):
ans=[[1,0],[0,1]]
fib = [[1, 1], [1, 0]]
while num:
if num%2:
ans=mul(ans,fib)
num=num>>1
fib=mul(fib,fib)
return ans
def quickn1(num):
ans=[[1,0],[0,1]]
fib = [[1, 1], [1, 0]]
while num:
if num%2:
ans=mul1(ans,fib)
num=num>>1
fib=mul1(fib,fib)
return ans
if m>n+2:
print(quickn(n+2)[0][1]%p-1)
else:
print(quickn1(n+2)[0][1]%quickn1(m)[0][1]%p-1)#注意取模优化的顺序不可以错误二.波动数列
观察这个数列:
1 3 0 2 -1 1 -2 ...
这个数列中后一项总是比前一项增加2或者减少3。
栋栋对这种数列很好奇,他想知道长度为 n 和为 s 而且后一项总是比前一项增加a或者减少b的整数数列可能有多少种呢?
n,s,a,b=map(eval,input().split())
Mod=100000007
dp=[[0 for _ in range(1001)] for __ in range(1001)]
dp[1][(s%n+n)%n]=1 #第一项防止负数
for i in range(2,n+1):
sum_a=(n+1-i)*a%n
sum_b=(n+1-i)*b%n
for j in range(n):
dp[i][(j-sum_a+n)%n]=(dp[i-1][j]+dp[i][(j-sum_a+n)%n])%Mod
dp[i][(j+sum_b)%n]=(dp[i-1][j]+dp[i][(j+sum_b)%n])%Mod
print(dp[n][0])三.高僧斗法
古时丧葬活动中经常请高僧做法事。仪式结束后,有时会有“高僧斗法”的趣味节目,以舒缓压抑的气氛。
节目大略步骤为:先用粮食(一般是稻米)在地上“画”出若干级台阶(表示N级浮屠)。又有若干小和尚随机地“站”在某个台阶上。最高一级台阶必须站人,其它任意。(如图1所示)
两位参加游戏的法师分别指挥某个小和尚向上走任意多级的台阶,但会被站在高级台阶上的小和尚阻挡,不能越过。两个小和尚也不能站在同一台阶,也不能向低级台阶移动。
两法师轮流发出指令,最后所有小和尚必然会都挤在高段台阶,再也不能向上移动。轮到哪个法师指挥时无法继续移动,则游戏结束,该法师认输。
对于已知的台阶数和小和尚的分布位置,请你计算先发指令的法师该如何决策才能保证胜出
num=list(map(eval,input().split()))
nim=[]
ans=0
def is_win(n):
ans=0
for i in range(0,len(n),2):
ans^=n[i]
return ans
for i in range(1,len(num)):
nim.append(num[i]-num[i-1]-1)
if is_win(nim)==0:
print('-1')
else:
flag=False
for i in range(len(nim)):
for j in range(1,nim[i]+1):
nim[i]-=j
if i!=0:
nim[i-1]+=j
if is_win(nim)==0:
print("{} {}".format(num[i],j+num[i]))
flag=True
break
else:
nim[i]+=j
if i!=0:
nim[i-1]-=j
if flag:
break
四.2N皇后
给定一个n*n的棋盘,棋盘中有一些位置不能放皇后。现在要向棋盘中放入n个黑皇后和n个白皇后,使任意的两个黑皇后都不在同一行、同一列或同一条对角线上,任意的两个白皇后都不在同一行、同一列或同一条对角线上。问总共有多少种放法?n小于等于8。
G=[]
for i in range(n):
G.append(list(map(eval,input().split())))
ans=0
#print(G)
black=[-1 for i in range(n)]
white=[-1 for i in range(n)]
def put_white(num):
global G
global n
global white
global ans
global black
if num==n:
ans+=1
return
for i in range(n):
flag=True
white[num]=i
if black[num]==i:
continue
if G[num][i]==0:
continue
for j in range(num):
if white[j]==i or G[num][i]==0 or num-i==j-white[j] or num+i==j+white[j] :
flag=False
break
if flag:
put_white(num+1)
def put_black(num):
global G
global n
global black
if num==n:
put_white(0)
return
for i in range(n):
flag=True;
black[num]=i
if G[num][i]==0:
continue
for j in range(num):
if black[j]==i or G[num][i]==0 or num-i==j-black[j] or num+i==j+black[j]:
flag=False
break
if flag :
put_black(num+1)
put_black(0)
print(ans)
五.刷格子
X国的一段古城墙的顶端可以看成 2*N个格子组成的矩形(如下图所示),现需要把这些格子刷上保护漆。
你可以从任意一个格子刷起,刷完一格,可以移动到和它相邻的格子(对角相邻也算数),但不能移动到较远的格子(因为油漆未干不能踩!)
比如:a d b c e f 就是合格的刷漆顺序。
c e f d a b 是另一种合适的方案。
当已知 N 时,求总的方案数。当N较大时,结果会迅速增大,请把结果对 1000000007 (十亿零七) 取模。
n=eval(input())
mod=1000000007
ans=0
a=[0 for _ in range(n)]
b=[0 for _ in range(n)]
a[0]=1
b[0]=1
a[1]=6
b[1]=2
for i in range(2,n):
b[i]=2*b[i-1]
a[i]=2*b[i-1]+2*a[i-1]+4*a[i-2]
ans+=a[n-1]*4%mod#四个角
for i in range(1,n-1):
ans+=b[i]*a[n-i-2]*4
ans%=mod
ans+=4*b[n-i-1]*a[i-1]
ans%=mod
print(ans)
六.邮局问题(超时)
C村住着n户村民,由于交通闭塞,C村的村民只能通过信件与外界交流。为了方便村民们发信,C村打算在C村建设k个邮局,这样每户村民可以去离自己家最近的邮局发信。
现在给出了m个备选的邮局,请从中选出k个来,使得村民到自己家最近的邮局的距离和最小。其中两点之间的距离定义为两点之间的直线距离。
import math
def dfs(now,num,sum_dis,min_dist):#
global k,curr_dis,curr_post,flag,dist_m,m,n
if k-num>m-now:
return
if now>m-1 and numk:
return
if num==k:
if curr_dis>sum_dis:
curr_dis=sum_dis
for i in range(k):
ans[i]=curr_post[i]
return
min_dist2=[i for i in min_dist]
dfs(now+1,num,sum_dis,min_dist2)
if flag[now]==1:
return
curr_post[num]=now
temp=False
if num==0:
for i in range(n):
min_dist[i]=dist_m[now][i]
sum_dis+=dist_m[now][i]
temp=True
else:
for i in range(n):
if min_dist[i]>dist_m[now][i]:
sum_dis -= min_dist[i]
sum_dis+=dist_m[now][i]
min_dist[i]=dist_m[now][i]
temp=True
if temp==False:
flag[now]=1
else:
dfs(now+1,num+1,sum_dis,min_dist)
return
n,m,k=map(eval,input().split())
peo=[]
post=[]
for i in range(n):
peo.append(list(map(eval,input().split())))
for i in range(m):
post.append(list(map(eval,input().split())))
dist_m=[[math.sqrt((peo[i][0]-post[j][0])*(peo[i][0]-post[j][0])+(peo[i][1]-post[j][1])*(peo[i][1]-post[j][1])) for i in range(n)] for j in range(m)] #行为邮局 列为居民
ans=[-1 for i in range(k)]
dis_r=[-1 for i in range(n)] #当前已知的到某村庄的距离
curr_dis=float('inf')
curr_post=[-1 for i in range(k)]
flag=[0 for i in range(m)]
dfs(0,0,0,dis_r)
for i in ans:
print(i+1,end=' ') 七.回形取数
回形取数就是沿矩阵的边取数,若当前方向上无数可取或已经取过,则左转90度。一开始位于矩阵左上角,方向向下。
m,n=map(eval,input().split())
G=[]
for _ in range(m):
G.append(list(map(eval,input().split())))
flag=[[0 for _ in range(n)] for __ in range(m)]
def dfs(i,j,mod):#mod 三种模式,0往下,1往右,2往上,3往左
global G,flag,m,n
print(G[i][j],end=' ')
flag[i][j] = 1
if mod==0:
while i+1=0 and flag[i-1][j]==0:
dfs(i-1,j,2)
elif mod==2:
while i-1>=0 and flag[i-1][j]==0:
i-=1
print(G[i][j],end=' ')
flag[i][j] = 1
if j-1>=0 and flag[i][j-1]==0:
dfs(i,j-1,3)
else:
while j-1>=0 and flag[i][j-1]==0:
j-=1
print(G[i][j],end=' ')
flag[i][j] = 1
if i+1 八.矩阵快速幂
给定一个N阶矩阵A,输出A的M次幂(M是非负整数)
例如:
A =
1 2
3 4
A的2次幂
7 10
15 22
n,N=map(eval,input().split())
M=[]
for _ in range(n):
M.append(list(map(eval,input().split())))
ans=[[0 for _ in range(n)] for __ in range(n)]
for i in range(n):
ans[i][i]=1
def mul(a,b):
i=len(a)
j=len(b[0])
ans=[[0 for _ in range(j) ] for __ in range(i)]
for ii in range(i):
for jj in range(j):
for k in range(len(a[0])):
ans[ii][jj]+=(a[ii][k]*b[k][jj])
return ans
while N:
if N%2==1:
ans=mul(ans,M)
N//=2
M=mul(M,M)
for i in range(n):
for j in range(n):
print(ans[i][j],end=' ')
print()
九.最大子序列和
对于一个给定的长度为N的整数序列A,它的“子序列”的定义是:A中非空的一段连续的元素(整数)。你要完成的任务是,在所有可能的子序列中,找到一个子序列,该子序列中所有元素的和是最大的(跟其他所有子序列相比)。程序要求你输出这个最大值。
n=eval(input())
num=list(map(eval,input().split()))
ans=-float('inf')
temp=0
for i in range(len(num)):
temp+=num[i]
if temp>ans:
ans=temp
if temp<0:
temp=0
print(ans)十.最优的代价
回文串,是一种特殊的字符串,它从左往右读和从右往左读是一样的。小龙龙认为回文串才是完美的。现在给你一个串,它不一定是回文的,请你计算最少的交换次数使得该串变成一个完美的回文串。
交换的定义是:交换两个相邻的字符
例如mamad
第一次交换 ad : mamda
第二次交换 md : madma
第三次交换 ma : madam (回文!完美!)
from collections import defaultdict
n=eval(input())
s=input()
num_dic=defaultdict(int)
num=0
list_s=[]
for i in range(n):
list_s.append(s[i])
num_dic[s[i]]+=1
if num_dic[s[i]]%2==1:
num+=1
else:
num-=1
ans=0
if num>1:
print('Impossible')
else:
if num==1 and n%2==0:
print('Impossible')
else:
for i in range((n-1)//2):
if list_s[i]!=list_s[n-i-1]and num_dic[list_s[i]]%2==0:
for j in range(n-i-1,i,-1):
if list_s[j]==list_s[i]:
ans+=(n-i-1)-j
del list_s[j]
list_s.insert(n-i-1,list_s[i])
break
if list_s[i] != list_s[n - i - 1] and num_dic[list_s[i]] % 2 == 1:
for j in range(i, n - i - 1):
if list_s[j] == list_s[n - i - 1]:
ans += abs(j - i)
del list_s[j]
list_s.insert(i, list_s[i])
break
print(ans)
ss=''.join(list_s)
print([ i for i in range(n) if ss[i]!=ss[n-i-1]])
print(ss)
print(num_dic)
十一.3000米排名预测(dfs加剪枝,全排列)
3000米长跑时,围观党们兴高采烈地预测着 最后的排名。因为他们来自不同的班,对所有运动员不一定都了解,于是他们分别对自己了解的一些运动员的实力作出了评估,即对部分运动员做了相对排名的预 测,并且告诉了可怜留守的班长。因为无聊,于是他们就组团去打Dota去了。比赛结束后他们向班长询问最后的排名,但班长不记得了,只记得他们中哪些人的 预测是正确的,哪些人的预测是错误的。他们想知道比赛的排名可能是什么。
from collections import defaultdict
n,m=map(eval,input().split())
pass_by=[]
for _ in range(m):
pass_by.append(list(map(eval,input().split())))
num_dic=defaultdict(int)
t=[i[1:len(i)-1] for i in pass_by if i[len(i)-1]==1]
f=[i[1:len(i)-1] for i in pass_by if i[len(i)-1]==0]
flag_t=[0 for _ in range(len(t))]
ans=[]
def wrong(nums):
global f
for i in f:
ii=0
jj=0
while ii十二.分分钟的碎碎念
以前有个孩子,他分分钟都在碎碎念。不过,他的念头之间是有因果关系的。他会在本子里记录每一个念头,并用箭头画出这个念头的来源于之前的哪一个念头。翻开这个本子,你一定会被互相穿梭的箭头给搅晕,现在他希望你用程序计算出这些念头中最长的一条因果链。
将念头从1到n编号,念头i来源于念头from[i],保证from[i]< i,from[i]=0表示该念头没有来源念头,只是脑袋一抽,灵光一现。
n=eval(input())
nums=[0]
for _ in range(n):
nums.append(eval(input()))
ans=0
def dfs(i,now):
global nums,ans
if i==0:
if now>ans:
ans=now
return
else:
dfs(nums[i],now+1)
for i in range(n-1,0,-1):
dfs(nums[i],1)
print(ans)
十三.带分数(回溯dfs超时,得25分)
100 可以表示为带分数的形式:100 = 3 + 69258 / 714。
还可以表示为:100 = 82 + 3546 / 197。
注意特征:带分数中,数字1~9分别出现且只出现一次(不包含0)。
类似这样的带分数,100 有 11 种表示法。
n = int(input())
count = 0
se = {'1', '2', '3', '4', '5', '6', '7', '8', '9'}
def check(x, no_used):
s = str(x)
cf = set()
for i in range(len(s)):
if s[i] in cf or s[i] not in no_used:
return 0
cf.add(s[i])
return 1
for i in range(1, n):
if not check(i, se):
continue
used = {x for x in str(i)}
no_used1 = se - used
for j in range(1, 10**len(no_used1)):
if not check(j, no_used1):
continue
k = (n - i) * j
if len(str(k)) > (len(no_used1) - len(str(j))): #长度判断 非常重要的一句话!!!! 如果不加的话时间必定超限
break
used = {x for x in str(j)}
no_used2 = no_used1 - used
if check(k, no_used2) and len(no_used2) == len(str(k)):
count += 1
print(count)十四.最大子阵(超时,算法和其他语言的一样,55分)
给定一个n*m的矩阵A,求A中的一个非空子矩阵,使这个子矩阵中的元素和最大。
其中,A的子矩阵指在A中行和列均连续的一块。
n,m=map(eval,input().split())
martix=[]
for _ in range(n):
martix.append(list(map(eval,input().split())))
sum_num=[[ 0 for _ in range(m)] for __ in range(n+1)]
for i in range(1,n+1):
for j in range(m):
sum_num[i][j]=martix[i-1][j]+sum_num[i-1][j]
ans=0
for i in range(1,n+1):
for j in range(i,n+1):
sum_n=0
for k in range(m):
sum_n +=sum_num[j][k]-sum_num[i-1][k]
if sum_n>ans or ans==0:
ans=sum_n
if sum_n<0:
sum_n=0
print(ans)