分段插值方法和code，cubic spline, cubic hermite spline

0. 引入

在 Non-Rigid Dense Correspondence with Applications for Image Enhancement 和 Exposure Stacks of Live Scenes with Hand-Held Cameras中 使用了分段函数拟合的方法: cubic spline 和 cubic hermite spline。
cubic是三次插值函数，每一段都是cubic函数，连接在一起构成spline.

1.Cubic Spline Interpolation

Cubic Spline Interpolation清晰的讲解和python示例

from scipy.interpolate import CubicSpline
import numpy as np
import matplotlib.pyplot as plt

plt.style.use('seaborn-poster')
x = [0, 1, 2]
y = [1, 3, 2]

# use bc_type = 'natural' adds the constraints as we described above
f = CubicSpline(x, y, bc_type='natural')
x_new = np.linspace(0, 2, 100)
y_new = f(x_new)
plt.figure(figsize = (10,8))
plt.plot(x_new, y_new, 'b')
plt.plot(x, y, 'ro')
plt.title('Cubic Spline Interpolation')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

2. 多项式插值

多项式插值，顾名思义，即以一个多项式的形式来刻画经过一系列点的曲线。
比如拉格朗日插值 和牛顿插值，无论是Lagrange插值还是Newton插值，本质都是用一个多项式来进可能精确地描绘过节点的原始函数。但多项式插值的矛盾之处在于，若节点太少，则插值出来的函数与原始函数可能偏离较大，返回的插值结果对于实际的指导用处不大；但若节点太多，则多项式的阶数也会需要相应增加，但太高的阶数容易又会导致绘制出的插值曲线在边缘处不稳定，这便是龙格现象

不同插值方法的比较及Python实现

3. 分段插值

多项式插值容易产生龙格现象，这时候可以使用分段插值。

常见的分段插值主要有分段线性插值，分段三次Hermite插值以及分段三次样条插值。
下面的博客介绍的很清楚：
参考
1.不同插值方法的比较及Python实现
2. Cubic Hermite Spline之二
3. 可以指定函数值和斜率的cubic hermite spline python lib

from chspy import CubicHermiteSpline
from matplotlib.pyplot import subplots

spline = CubicHermiteSpline(n=3)

#            time   state    slope
spline.add((   0 , [1,3,0], [0,1,0] ))
spline.add((   1 , [3,2,0], [0,4,0] ))
spline.add((   4 , [0,1,3], [0,4,0] ))

fig,axes = subplots(figsize=(7,2))
spline.plot(axes)
axes.set_xlabel("time")
axes.set_ylabel("state")
fig.legend(loc="right",labelspacing=1)
fig.subplots_adjust(right=0.7)

得到：

4. Monotone Cubic Interpolation单调的分段插值code

4. scipy.interpolate中的插值方法

4.1 cubic hermite spline插值类

class scipy.interpolate.CubicHermiteSpline
class scipy.interpolate.PchipInterpolator 单调

4.2 cubic spline插值类

class scipy.interpolate.CubicSpline
class scipy.interpolate.Akima1DInterpolator 完全通过给的点

Akima1DInterpolator拟合分段三次多项式，给定向量x和y。生成的曲线通过给定的数据点，看起来平滑自然。
仅用于精确的数据，因为拟合曲线精确地通过给定的点。

'''
cubic hermite :节点处一阶导数相等
cubic :节点处二阶导数相等，因此更加平滑，更加扭曲
Akima1DInterpolator ： cubic 分段插值，但是拟合的曲线会通过给定点
PchipInterpolator :monotonic cubic hermite ,在分段区间内都是单调的。
'''

4.3 示例和代码：

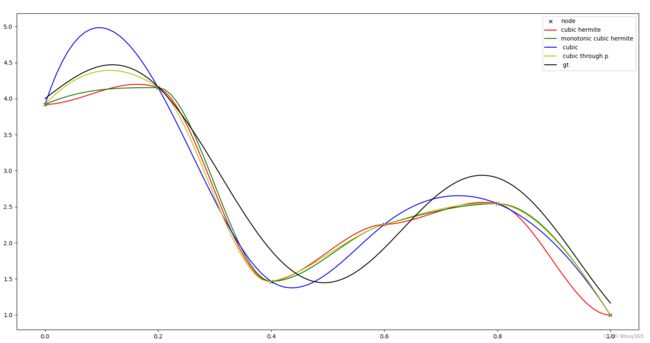
gt是groundtruth 曲线
node是生成的带噪声的点

其他是使用上面4个函数拟合得到曲线。

完整code 如下：

"""
分段函数拟合
"""
import numpy as np
import scipy
from matplotlib import pyplot as plt

def fun(xx, fig=0):
    # xx = np.linspace(0, 1, 100)
    yy1 = np.sin(xx * 10)
    yy2 = (xx - 2) ** 2 * np.sqrt(xx ** 4 + 1)
    yy3 = xx / 10.4 * np.log(20 * xx ** 2 + 1)

    yy = yy1 + yy2 + yy3
    if fig:
        plt.figure()
        plt.plot(xx, yy1, 'r-', xx, yy2, 'g-', xx, yy3, 'b-', xx, yy, 'k-')
        plt.show()
    return yy
if __name__ == "__main__":
    xx = np.linspace(0, 1, 100)
    yy = fun(xx, 1)

    np.random.seed(2)
    xx1 = np.linspace(0, 1, 6)
    yy1 = fun(xx1) + np.random.randn(len(xx1)) * 0.2
    plt.figure()
    plt.plot(xx1, yy1, 'r+', xx, yy, 'k-')
    plt.show()

    dy = np.zeros_like(yy1)
    dy[:-1] = yy1[1:] - yy1[:-1]
    interp_1 = scipy.interpolate.CubicHermiteSpline(xx1, yy1, dy )
    yy_pred_1 = interp_1(xx)

    interp_1 = scipy.interpolate.PchipInterpolator(xx1, yy1)
    yy_pred_2 = interp_1(xx)

    interp_1 = scipy.interpolate.CubicSpline(xx1, yy1)
    yy_pred_3 = interp_1(xx, 0)

    interp_1 = scipy.interpolate.Akima1DInterpolator(xx1, yy1)
    yy_pred_4 = interp_1(xx)

    plt.figure()
    plt.plot(xx1, yy1, 'kx', label='node')
    plt.plot( xx, yy_pred_1, 'r-', label='cubic hermite')
    plt.plot( xx, yy_pred_2, 'g-', label='monotonic cubic hermite')
    plt.plot( xx, yy_pred_3, 'b-', label=' cubic ')
    plt.plot(xx, yy_pred_4, 'y-', label=' cubic through p')
    plt.plot(xx, yy, 'k-', label=' gt')
    plt.legend()
    plt.show()
    '''
    cubic hermite :节点处一阶导数相等
    cubic :节点处二阶导数相等，因此更加平滑，更加扭曲
    Akima1DInterpolator ： cubic 分段插值，但是拟合的曲线会通过给定点
    PchipInterpolator :monotonic cubic hermite ,在分段区间内都是单调的。
    '''