明文加密、消息摘要、数字签名、数字证书
参考文献:What is a Digital Signature?
Bob 拥有两个不一样的密钥
其中一个叫做公钥,另一个叫做私钥
任何需要的人都能获得 Bob 的公钥,但只有 Bob 拥有私钥
密钥用来加密数据,加密的意思是改变数据的存储形式使其不可读,只有拥有正确密钥的人才能把数据变回可读的形式
Bob 的两个密钥都能用来加密数据,其中一个将数据加密后,只能用另一个来解密
用于加密和解密的密钥不同时,称为非对称加密,相同时称为对称加密
只有在非对称加密中,区分私钥和公钥才有意义
因为如果密钥相同,那么就只能要么公开密钥要么不公开,没办法公开一个保密另一个
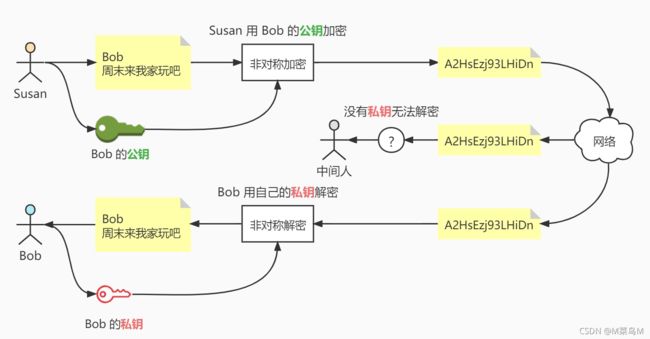
Susan 可以用 Bob 的公钥加密消息,然后发送给 Bob
Bob 用自己的私钥来解密消息
任何没有私钥的人在消息传输途中截获到密文都无法解密数据,因此都无法读懂消息的内容
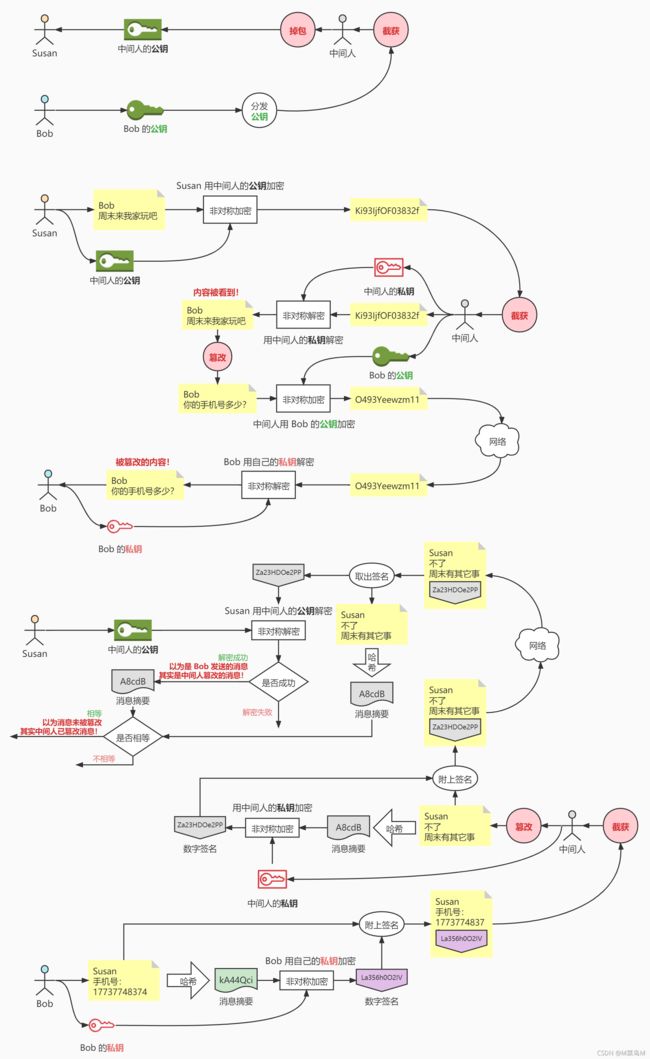
Bob 可以使用私钥和正确的软件在发送的数据中附加数字签名
数字签名是一个附在数据上的 Bob 独有的 “ 印章 ”,难以伪造
另外,数字签名还可以确保任何对数据的修改都能被发现
要给一个文档签名,Bob 的软件首先会通过 “ 哈希 ” 将数据压缩到几行中
这几行被称为消息摘要(没有办法将消息摘要变回原来的数据)
哈希(Hash)一般翻译为散列、杂凑,或音译为哈希
是把任意长度的输入(又叫做预映射 pre-image)通过散列算法变换成固定长度的输出,该输出就是散列值
这种转换是一种压缩映射,也就是,散列值的空间通常远小于输入的空间,不同的输入可能会散列成相同的输出,所以不可能从散列值来确定唯一的输入值
简单的说就是一种将任意长度的消息压缩到某一固定长度的消息摘要的函数
Bob 的软件接着会用 Bob 的私钥对消息摘要进行加密,加密的结果就是数字签名
最后,Bob 的软件会将数字签名附加到文档中
Bob 将签名后的文档发送给 Susan
Susan 的软件接收到消息后,先用 Bob 的公钥对数字签名解码
如果解码成功,说明这是 Bob 签的名,因为只有 Bob 有私钥
Susan 的软件然后对文档进行哈希,得到消息摘要
如果解码得到的消息摘要与哈希文档得到的消息摘要不同,说明文档或摘要被人修改过
如果相同,则说明要么数据未被修改过,要么数据被修改为了与源文档发生哈希冲突的值(可以忽略)
因为存在哈希冲突,不同的原文可能产生相同的哈希值(概率很小)
因此,对消息做哈希的结果和消息附带的消息摘要相同,不能百分百证明消息一定未被修改过
但是这种情况只存在于消息恰好被修改为了与其发生哈希冲突的数据的情况
一是概率非常小,二是这种修改方式本身是固定的修改,难以达到篡改内容误导接收者的目的(如果只是为了妨碍通信,完全可以随意修改)
因此一般来说,当消息与消息摘要相同时,都认为消息没有被篡改过
而且,反过来说,同一个消息,不可能产生不同的哈希值
因此当接收到的原文做哈希后和接收到的消息摘要不一样时,一定说明消息或者摘要被篡改过
小结:
- 明文加密:为了不被中间人窃取内容
- 消息摘要:为了验证消息是否被篡改
- 数字签名:为了验证发送者的身份
其中,明文加密与数字签名都是利用非对称加密来完成的,要达到目的,必须保证两点:
- 私钥没有泄露
- 公钥是真的,即分发公钥时,没有被中间人掉包
关于第一点,每次密钥对都由私钥持有者生成,由私钥持有者自己保证私钥的保密性
关于第二点,私钥持有者如果面对面亲手把生成的公钥交给需要公钥的人
那么获得公钥的人有理由相信这个公钥是真的,可以放心地使用
但问题在于,在如今网络时代的多数场景下,出于效率的原因,是不会面对面分发公钥的,一般都是通过网络进行分发
那么在分发公钥时,公钥就有可能在途中被截获并掉包
此时,需要通过一个证书颁发机构为 Bob 提供公钥的数字证书来证明 Bob 公钥的真实性和有效性
数字证书上有关于 Bob 身份的信息,用于核对 Bob 身份
还有 Bob 公钥的信息,例如过期时间、状态等,用于表示证书上的这个 Bob 的公钥处于什么状态
同时,数字证书上也有用证书颁发机构的私钥加密的数字签名,可用来验证颁发机构的身份和数字证书是否被篡改
任何人需要使用 Bob 的公钥时,都应该向证书颁发机构请求获取 Bob 的数字证书(因为存在过期时间等时间相关的元素,所以应该每次都请求)
然后用证书机构的公钥验证证书颁发机构的身份以及证书是否被篡改(假设证书颁发机构的公钥是通过安全渠道获得的,比如系统预装的)
对证书颁发机构验证成功后,再根据数字证书上的信息检查 Bob 这个公钥的有效性
如果有效则可直接使用数字证书上的这个 Bob 的公钥
现实中,可以对以上过程进行多次嵌套
例如机构 A 为机构 B 的公钥发证书,机构 B 为机构 C 的公钥发证书,机构 C 为 Bob 的公钥发证书
因为中间人需要知道所有的分发验证关系,并把所有的会话正确关联起来才能成功完成掉包、窃取以及篡改
所以嵌套得越多,理论上中间人成功的难度就越高
加上证书是有过期时间的,因此可以通过这种方式大大提高安全性
非对称加密算法的加密解密过程效率不高,当要加密的内容很长时,加密时间也会很长
由于数字签名是对哈希后固定长度的哈希值进行加密,因此非对称加密在数字签名验明身份与防篡改方面没有问题
但是用来给任意长度的明文加密,以防止传输内容被三方获取,并不适合用非对称加密,因为那样加解密时间太长
通常的做法是,用对称加密来对明文进行编码防止内容泄露
而用非对称加密的方式来分发对称加密中用到的密钥(HTTPS)
非对称加密有效的前提是在没有正确密钥时无法解密
而这一点的本质是由大数据因数分解在数学上的困难性决定的
两种情况可能会对此构成威胁:
- 可能已经有人在数学上找到了高效地计算大数据因数分解的方法,只是出于国家利益没有公布出来
- 量子计算在数学层面已经有高效计算大数据因数分解的算法,在物理上也已经制造出了能够计算较小数据因数分解的量子计算机,加之各国在量子信息上的大力投入,可以预见在不久的将来,非对称加密将不再保险
量子保密通信可以解决上述问题,用量子信道分发与原文同样长度的随机密钥
用随机密钥与明文进行按位异或,明文也就变成了完全随机的字节序列,然后就可以在传统信道上传输而不怕被破解了
因为整个过程都是建立在物理原理上的,并不会被人用数学方式破解
目前量子保密通信的信道已经建成并得到了验证,只是目前分发随机密钥的效率还比较低
不过可以用量子保密通信来分发对称加密的密钥,然后用对称加密来加密明文
参考文献:What is a Digital Signature?