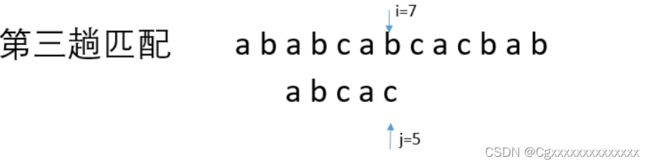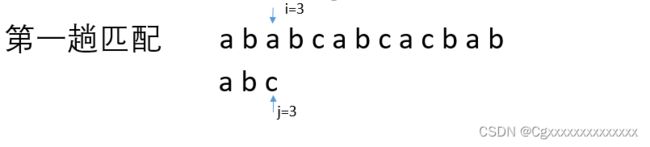KMP算法以及KMP算法的优化

KMP算法是基于串的模式匹配的一种比较时间复杂度较低的一种算法。

那么什么是模式匹配以及KMP算法究竟好在哪里呢？

串的模式匹配：子串的低位操作通常称为串的模式匹配，它求的是子串（模式串）在主串中的位置。

我们这里对串的两种模式匹配进行一下对比

第一种就是简单的模式匹配算法

简单的模式匹配算法是很容易理解也是大部分同学常用的算法，也可以说是暴力匹配算法

我们这里简单描述一下暴力匹配的算法思想

分别用技术指针i和j只是主串S和模式串（子串）T中当前正待比较的字符位置

算法思想为：从主串S的第一个字符起，与模式串T的第一个字符比较，若相等，则继续逐个比较后续字符，否则从主串的下一个字符起重新和模式串的字符比较，以此类推，直至模式串T中的每个字符在主串S中的一个连续字符序列相等，则称匹配成功，返回的函数值为与模式串T中第一个字符相等的字符在主串S中的序号，否则称匹配不成功，返回的函数值为0。

算法实现如下

int Index(String S,String T){
    int i=1,j=1;
    while(i<=S.length && j<=T.length){
        if(S.ch[i]==T.ch[j]){
            ++i;
            ++j;
        }
        else{
            i=i-j+2;
            j=1
        }
    }
    if(j>T.length){
        return i-T.length;
    }else{
        return 0;
    }
}

下图充分展示了模式串T=‘abcac’和主串S匹配的过程

这便是常用的暴力匹配算法，显然我们的主串指针i遇到不符合模式串T的情况时需要回溯这就大大降低了我们的匹配效率

设主串长度为m，模式串长度为n

由此可以的出暴力匹配算法最差的时间复杂度为O（mn）

那么有没有不需要主串i回溯的算法进行匹配呢

这时我们的KMP算法就该登场了

由D.E.Knuth，J.H.Morris和V.R.Pratt提出的算法，因此人们称它为克努特—莫里斯—普拉特操作（简称KMP算法）。KMP算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的

刚刚我们便说了，KMP算法核心思想是利用匹配失败后的信息尽量减少模式串与主串的匹配次数

这时候我想引用刚刚我们暴力匹配上图的第三趟匹配，如图所示

 由图可以知道我们的b和c是不能够匹配成功的那么既然不想让主串的指针i进行回溯

假设i只能往后移动那么此时的模式串abcac应该从哪里匹配呢

显然如果我们的j再回到1利用主串的b和模式串的a进行匹配是不合理的

因为此时的i=7指向的b

但是如果j=1指向模式串的a就忽略了主串中位序为6即i=6的a

而恰好可以看出模式串在主串的位置正是由i=6开始的

如果重新赋值j=1的话那么就不会匹配成功

所以此时的j应该是等于2再对i=7进行匹配

 即i=7与j=2进行匹配

可以的出两个字符是相等的继而进行i++和j++直到j大于了模式串T的长度退出

便是匹配成功

可知KMP算法主串的指针不会回溯

而模式串的指针也是根据一定规则进行回溯的

这样就大大减少了不必要的匹配

那么针对不同的模式串我们以什么依据什么规则进行对j的回溯调整呢

这时候我们要想了解模式串回溯的规则就要引用到一个新的概念

字符串的前缀、后缀和部分匹配值

前缀指除了最后一个字符以外，字符串的所有头部子串

后缀指除了第一个字符以外，字符串的所有尾部子串

部分匹配值则为字符串的前缀和后缀最长相等的前后缀长度

下面我们以模式串‘abcac’在主串中的匹配为例进行说明

如何手动计算部分匹配值

如下图第一趟匹配

当我们匹配到a与c进行比较时

发现a与c并不同所以我们的模式串需要回溯，回溯的位置就要看我们模式串当前指向的位置c前面的部分子串

由此可见c前面的子串为ab并且是匹配的

要求ab的部分匹配值我们需要知道ab的前缀和后缀

根据我们刚才对前缀和后缀的定义

ab的前缀为{a}，后缀为{b}

而部分匹配值为字符串的前缀和后缀最长相等的前后缀长度

而abc的前后缀并没有相等的子串所以匹配长度为0 

在实际KMP算法中，为了使公式简洁，计算简单，如果串的位序是从1开始的，则我们计算的部分匹配值就要整体加1，如果串的位序是从0开始的，则next数组不需要整体加1

为了方便大家理解这里我做整体加1处理

刚刚我们说的ab的部分匹配值为0，我们进行加1处理，那么部分匹配值为1

此时的这个部分匹配值即为我们的j所要回溯到的位置即j=1，指向a的位置继续与主串中的i=3指向的位置进行比较

由此可见我们就省略了暴力匹配中的第二趟的匹配，来到了第三趟的匹配

我们继续来看第三趟的匹配

如图所示

此时我们的b和c又匹配不相符了那么我们的i继续保持不变，只回溯j，那么j应该回溯到哪里呢

就要看当前j指向的c前面的部分子串即‘abca’并且是与主串匹配的

我们继续来利用‘abca’的前缀和后缀来求部分匹配值

abca的前缀分别为：{a}，{ab}，{abc}

abca的后缀分别为：{a}，{ca}，{bca}

最长相等前后缀长度为1

因为我们的位序是从1开始的所以部分匹配值需要加1

所以这里的部分匹配值为2即为我们的j需要指向的位序就是模式串中的b

进而继续完成匹配

我们在这里总结一下关于‘abcac’求部分匹配值的表格用来帮助理解

串	前缀	后缀	最长相等前后缀长度
‘a’	∅	∅	0
‘ab’	a	b	0
‘abc’	a，ab	c，bc	0
‘abca’	a，ab，abc	a，ca，bca	1
‘abcac’	a，ab，abc，abca	c，ac，cac，bcac	0

而我们算出的最长相等前后缀长度以及匹配值如何应用到程序中，就需要我们建立一个数组来存储最长相等前后缀长度或者是匹配值

我们暂且定义为数组next

那么如果按我这种理解，位序从1开始计算那么next[]={0,1,1,2,1}

也许有疑问为什么next[0]=0呢

因为当next[0]=0的时候说明我们的模式串第一个字符就与当前主串中的位置不匹配

用来提醒主串中的指针此时应该往后移动了

这里会在我们下面的程序中进行体现

int KMP(String S,String T,int next[]){
	int i=1,j=1;
	while(i<=S.length&&j<=T.length){
		if(j==0||S.ch[i]==T.ch[j]){
			++i;
			++j;
		}else{
			j=next[j];
		}
		if(j>T.length){
			return i-T.length;
		}else{
			return 0;
		}
	}
}

我们只是手动计算了next数组，其实KMP算法最主要的还是求解next数组，与求解next数组相比，KMP匹配算法相对要简单一些

它与简单的模式匹配很相似，不同之处仅在于当匹配过程失效时，指针i保持不变，指针j退回到next[j]的位置并重新进行比较，当指针j=0时，使指针i和j同时加1，即如果主串的第i个位置与模式串的第一个字符不等，则应从主串的第i+1个位置开始匹配。

这里写一份求解next数组的程序供大家参考，程序还是以模式串abcac为例进行求解next数组

虽然模式串只有5个字符但是还是程序比较绕的，需要多理解几遍。

void get_next(String T,int next[]){
	int i=1,j=0;
	next[1]=0;//直接将next[1]赋0，为了方便理解我们的next[0]不用 
	while(i<=T.length){
		if(j==0||T.ch[i]==T.ch[j]){//注意这里的i和j都是指向的模式串的字符进行对比 
			++i;
			++j;
			next[i]=j;
		}else{
			j=next[j];
		}
	}
}
//可以针对abcac进行推几遍自己得出next数组
//当然这里的next数组是整体进行了加1处理的 
//而我们在上文中的表格手动计算的并没有进行加1处理 

所得到的next数组也为next[]={0,1,1,2,1}

然后根据next数组来进行KMP算法

由此可以看出KMP的时间复杂度为O(m+n)

但是一般情况下普通匹配实际执行时间近似为O(m+n)因此至今仍被采用

KMP算法在主串与子串有很多部分匹配时才显得比普通算法要快的多

其主要优点是主串不回溯。