力扣刷题每日打卡

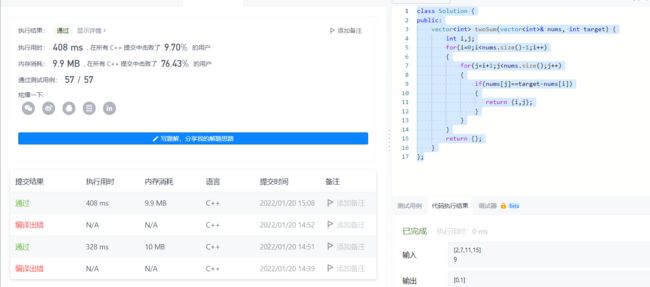
2022-01-20 1. 两数之和

今天刚开始刷力扣，感觉都是怪怪的

class Solution {
public:
    vector twoSum(vector& nums, int target) {
        int i,j;
        for(i=0;i

这里为什么可以直接return{} 呢?

因为是新型的intpair

这个用法我从来没见过,于是上网查找到了一个比较好的答案:

只要构造函数不是explicit的，就可以在newInteger中调用return i而非return Integer(i)这种复杂的表达。

但是假如现在有个新类型IntPair，其构造函数有2个int呢？那么只能乖乖的return IntPair(i, j)来返回了，有了列表初始化后就可以直接return {i, j}了。

至于为什么不弄个像return i, j或者return (i, j)这样的语法？ 因为在C语言存在逗号表达式，也就是说i,j其实是对i和j的逗号表达式，返回的是j。C++兼容了C（至少是旧标准），因此得另辟蹊径简化代码。

使用迭代器find

class Solution {
public:
    vector twoSum(vector& nums, int target) {
        int i,j;
        vector last;
        vector::iterator it;
        for(i=0;i

这里使用find ，find结果仍然是一个迭代器，只不过是指向不同位置了，

it-nums.begin 迭代器相减获得的是两个的相位差，也就是始终it-0 获得it的距离

使用Map优化

unordered_map 能够更方便的进行查找

class Solution {
public:
    vector twoSum(vector& nums, int target) {
        std::unordered_map hash; //定义一个哈希表
        for(int i=0;i::iterator it = hash.find(target-nums[i]);
            if(it!=hash.end()){ //如果找到了
                return {it->second, i}; //返回两个下标
            }
            //没找到，就放入哈希表 key = nums[i],value = i; 方便查找
            hash[nums[i]] = i;
        }
        return {};
    }
};

事实证明，unorderd_map 更适合查询，因为是优化过的红黑树

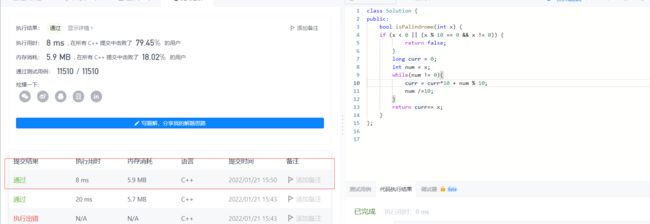
2022-01-21 回文数

class Solution {
public:
    bool isPalindrome(int x) {
        if(x < 0){
            return false;
        }
        long curr = 0;
        int num = x;
        while(num != 0){
            curr = curr*10 + num % 10;
            num /=10;
        }
        return curr== x;
    }
};

比较简单，每次取出个位，然后整一个变量，给他倒置

当然我们可以做优化，也就是说，10的倍数，明显不能够作为回文数，

或者，奇数个数字，中间的一半即可， 并不需要全部都转置

class Solution {
public:
    bool isPalindrome(int x) {
    if (x < 0 || (x % 10 == 0 && x != 0)) {
            return false;
        }
        long curr = 0;
        int num = x;
        while(num != 0){
            curr = curr*10 + num % 10;
            num /=10;
        }
        return curr== x;
    }
};

虽然仅仅优化了一点，但是时间减少了很多

2022 1.22 打RW摆烂

2022-01-23 13. 罗马数字转整数

class Solution {
public:
    int romanToInt(string s) {
        int store;
        int result=0;
        //打表
        unordered_map table = {{"I", 1}, {"IV", 4}, {"V", 5}, {"IX", 9},
         {"X", 10}, {"XL", 40}, {"L", 50}, {"XC", 90}, {"C", 100}, {"CD", 400}, 
         {"D", 500}, {"CM", 900}, {"M", 1000}};
        int size  = int(s.size());
        for(int i=0;i

2022-01-24 最长公共前缀

因为有多个，比较两个是最为方便的，因此，写好一个比较两个的即可

class Solution {
public:
    string compare(const string& str1,const string& str2){
        int ssize = (str1.size() > str2.size()) ? str2.size() : str1.size();
        string ans = "";
        for(int i=0;i& strs) {
     int size = strs.size();
     string vv = strs[0];
     if(size == 0){
         return "";
     }   
     for(int i =1;i

2022-01-25 有效的括号

这个是一个栈的题

class Solution {
public:
    bool isValid(string s) {
        stack sk;
        int n=int(s.size());
        if(n % 2 ==1)   //第一个条件，判断括号数为单数则ruturn false
        {
            return false;
        }
        unordered_map mp = {{'{','}'},{'(',')'},{'[',']'}};//方便查询
        for(char c:s){
            if(c == '(' || c == '[' || c == '{'){
                sk.push(c);
            }
            else{
                if (sk.empty()) return false;
                char top = sk.top();
                sk.pop();
                if(mp[top] == c){
                    continue;
                }else{
                    return false;
                }
            }

        }
        if (sk.empty()){
            return true;
        } else {
            return false;
        }
    }
};

2022-01-27 删除有序数组中的重复项

暴力

也就是把数组扫一遍，

前一个和后一个不同，就放在新的数组中，

双指针优化

class Solution {
public:
    int removeDuplicates(vector& nums) {
        int n =nums.size();
        if(n == 0){
            return 0;
        }
        int fast=1,slow=1;
        while(fast < n){
            if(nums[fast] != nums[fast-1] ){
                nums[slow] = nums[fast];
                ++slow;
            }
            fast++;
        }
        return slow;
    }
};

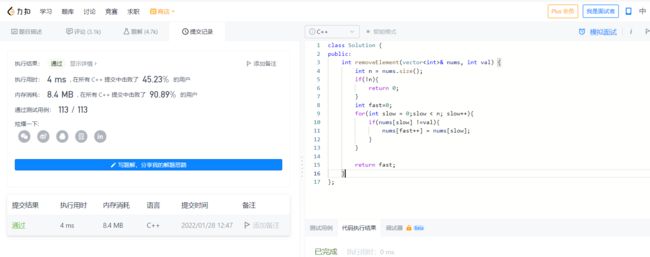
2022-01-28移除元素

和昨天的双指针一样

class Solution {
public:
    int removeElement(vector& nums, int val) {
        int n = nums.size();
        if(!n){
            return 0; 
        }
        int fast=0;
        for(int slow = 0;slow < n; slow++){
            if(nums[slow] !=val){
                nums[fast++] = nums[slow];
            }
        }
        
        return fast;
    }
};

2022-01-29 实现 strStr()

暴力

class Solution {
public:
    int strStr(string haystack, string needle) {
        int hay = haystack.size();
        int nee = needle.size();
        if(nee == 0){
            return 0;
        }
        for(int i = 0;i <= hay-nee ;i++){
            bool flag = true;
            for(int j = 0;j< nee;j++){
                if(haystack[i+j] != needle[j]){
                    flag = false;
                    break;
                }
            }
            if (flag) {
                return i;
            }
        }
        return -1;
    }
};

KMP算法

KMP算法最重要的是next数组

并不好理解，前缀表用来回退数组

前缀表是用来回退的，它记录了模式串与主串(文本串)不匹配的时候，模式串应该从哪里开始重新匹配。

这里理解不了。。。

鸽了

2022-1.39-2022-2.4 摸了

2022-02-05 搜索插入位置

class Solution {
public:
    int searchInsert(vector& nums, int target) {
       for(int i=0;i<=nums.size()-1;i++){
           if(nums[i] >= target){
               return i;
           }
       }
       return nums.size();
    }
};

一个简单的暴力，第一次区间写错了，导致空数组，

二分法

二分法找值，然后再pos位置补值

class Solution {
public:
    int searchInsert(vector& nums, int target) {
	int n = nums.size();
	int left = 0,right = n-1,ans = n;
	while(left<=right){
		int mid = ((right - left) >> 1)+left;
		if(target <=nums[mid]){
			ans = mid;
			right = mid -1;
		}else{
			left = mid+1;
		}
	}
	return ans;
    }
};

2022-02-06最大子数组和

开始想用前缀和来做，但是发现结果不对，没有考虑中间最大的情况，不是前缀和

class Solution {
public:
    static bool comp(int x ,int y)
    {
        return x > y;
    }

    int maxSubArray(vector& nums) {
        vector res;
        int x = 0;
        for(int i=0;i<=nums.size();i++){
            x+=nums[i];
            res.push_back(x);
        }
        sort(res.begin(),res.end(),comp);
        return res.front();
    }
};

转换思路

暴力

class Solution
{
public:
    int maxSubArray(vector &nums)
    {
        //类似寻找最大最小值的题目，初始值一定要定义成理论上的最小最大值
        int max = INT_MIN;
        int numsSize = int(nums.size());
        for (int i = 0; i < numsSize; i++)
        {
            int sum = 0;
            for (int j = i; j < numsSize; j++)
            {
                sum += nums[j];
                if (sum > max)
                {
                    max = sum;
                }
            }
        }

        return max;
    }
};

但是绝对会超时

动态规划

这里动态规划，它首先保证第一个值是初始值，然后，保证之前的每一个都是最大的，加起来就是最大的，否则的话，他就会把之前的数字清掉，然后换成当前的值，（这里是贪心）

动态规划

class Solution {
public:
    int maxSubArray(vector& nums) {
        int pre = 0;
        int ans = nums[0];
        for(int i=0;i

2022-02-07 58. 最后一个单词的长度

我们这里直接进行反向就可以，他要求最后一个字符串长度

class Solution {
public:
    int lengthOfLastWord(string s) {
        int length = s.size()-1;
        while(s[length] == ' '){
            length--;
        }
        int t=0;
        while(length >=0 && s[length] != ' '){
            length--;
            t++;
        }
        return t;
    }
};

这里有一个小tips

单引号是字符，一个字节，双引号是字符串有一个结束符，“b”是两个字节b + \0,而‘b’只有一个字节。

因此这里我们使用单引号

2022-02-08 66. 加一

找个题本质就是直接最后一位+1然后返回没什么操作难度

class Solution {
public:
    vector plusOne(vector& digits) {
        int size = digits.size();
        digits[size-1]+=1;
        return digits;
    }
};

这是一个简略版，只通过了91个样例

也就是说满十需要进1

做了一些补充修改后，发现有奇怪的事情出现了，99 需要100

做到这里我的思路可能就是一个for，暴力，找到大于10的，然后拆开插入

找了一个版本

倒序查看值是否为10，然后进一，变0，这个版本是0ms的

class Solution {
public:
    vector plusOne(vector& d) {
        int i = d.size()-1;
        ++d[i];
        while(d[i]==10){
            d[i]=0;
            if(i-1==-1){
                d.insert(d.begin(),1);
            }else{
                d[i-1]++;
                i--;  
            }
        }
        return d;               
    }
};

2022-02-09 爬楼梯

动态规划，使用滑动窗口思想

class Solution {
public:
    int climbStairs(int n) {
        int p=0,q=0,r=1;
        for(int i=0;i