概率&滤波器&图优化&最小二乘求解
文章目录
-
- SLAM后端优化
- 1 预知识点
-
- 1.1 高斯分布的正则形式(canonical form)及马氏距离:
- 1.2 状态方程的协方差及信息矩阵传递
- 1.3 信息矩阵和Hessian矩阵
- 1.4 协方差矩阵与信息矩阵
- 1.5 Schur补概念
- 1.6 信息矩阵的边缘化
- 1.7 贝叶斯后验滤波器
- 2 概率在线/全局SLAM算法
-
- 2.1 卡尔曼滤波(KF)
- 2.2 扩展卡尔曼滤波器(EKF)
- 2.3 UKF:TODO
- 2.4 Information Filter(IF)
- 2.5 Extended Information Filter (EIF)
- 2.6 粒子滤波器:粒子滤波器是贝叶斯滤波器的实现方式。
- 2.7 图(Graph)优化算法
- 2.8 SEIF算法
- 3 非线性优化
-
- 3.1 梯度矩阵Jacobians矩阵及Hessian矩阵
- 3.2 最速下降法
- 3.3 牛顿法:考虑函数向量的二阶导数
- 3.4 高斯牛顿法(GN)
- 3.5 LM(Levenberg-Marquadt)
- 3.6 信赖域法
- 4 解算工具介绍(ceres/g2o)
-
- 4.1 Ceres
- 4.2 G2o
- 4.3 GTSAM
- 5 参考
SLAM后端优化
前端估计有一定的误差,误差累积,将会造成很大的偏移误差。可以通过机器人传感器得到的环境信息(图像特征点/点云)来优化我们的估计,即机器人走一步,然后估计自己的运动,然后看周围,确定优化自己的位姿估计猜测。通过匹获得当前获得特征点(图像/点云)数据,我们可以得到一个新的位姿估计。有了更精确的估计,从而可以知道更精确的环境特征点分布。后端优化就是通过新的观测或者更充足的数据对前期粗略估计的结果进行优化。

在slam中要求解的变量包含传感器的位姿T及环境信息(地图点云) p p p。SLAM分为两种:在线SLAM及全局SLAM。
在线SLAM多以滤波器算法为主要实现方式。
在线SLAM算法维护变量:定义 k k k时刻优化变量 x k x_k xk:
x k = { T k , p 1 , ⋯ , p m } x_k=\left\{T_k,p_1,\cdots,p_m\right\} xk={Tk,p1,⋯,pm}
或者以李代数来表示相机的运动状态,则k时刻优化变量 x k x_k xk:
x k = { ξ k , p 1 , ⋯ , p m } x_k=\left\{\xi_k,p_1,\cdots,p_m\right\} xk={ξk,p1,⋯,pm}
全局SLAM算法维护所有变量:
x = { ξ 1 : k , p 1 : m } x=\left\{\xi_{1:k},p_{1:m}\right\} x={ξ1:k,p1:m}
1 预知识点
1.1 高斯分布的正则形式(canonical form)及马氏距离:
设多维变量 x ∼ N ( μ , Σ ) {x} \sim \mathcal{N}(\bm \mu,\ \ \Sigma) x∼N(μ, Σ)

其中:红色部分为常数项,可以归入归一化因子 η \eta η中。
![]()
令:
![]()
则可以用正则形式表示高斯分布: x ∼ N − 1 ( ξ , Λ ) {x}\sim\mathcal{N}^{-1}({\bm\xi}, {\Lambda}) x∼N−1(ξ,Λ)
![]()
其负log似然函数 g ( x ) g({x}) g(x)为:

其中 c c c为常数项, Λ \mathrm{\Lambda} Λ为半正定矩阵。
正则分布的负对数函数 g ( x ) g\left(\bm{x}\right) g(x)是关于x的二次型函数,且当 x = μ \bm{x}=\bm{\mu} x=μ时, g ( x ) g\left(\bm{x}\right) g(x)最小。

因此 g ( x ) g\left(\bm{x}\right) g(x)可以看作一种表征 x x x距离其中心值 μ \bm{\mu} μ的距离函数。这种加权二次距离函数叫做马氏距离(Mahalanobis distance)。
1.2 状态方程的协方差及信息矩阵传递
x ∼ N ( μ , Σ ) , y = A x + b x\sim\mathcal{N}\left(\mu,\Sigma\right),\ \ y=Ax+b x∼N(μ,Σ), y=Ax+b
则 y y y的分布的均值和方差满足:
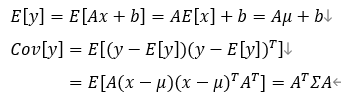
使用估计方程得到的估计变量 x ˉ k {\bar{x}}_k xˉk,优化后的变量为 x ^ k {\hat{x}}_k x^k。
1.3 信息矩阵和Hessian矩阵
Negative log likelihood的二阶导数(也就是其Hessian矩阵),正好是协方差的逆,即信息矩阵。
设多维变量 x ∼ N ( μ , Σ ) \bm{x} \sim \mathcal{N} (\bm{\mu},\ \ \Sigma) x∼N(μ, Σ)

其负log似然函数 g ( x ) g(\bm{x}) g(x)为:
![]()
g ( x ) g(\bm{x}) g(x)的Hessian矩阵为:
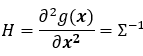
1.4 协方差矩阵与信息矩阵
高斯分布 N ( μ t , Σ t ) \mathcal{N}(\mu_t,\mathrm{\Sigma}_t) N(μt,Σt)可以写成canonical form(正则)形式: N − 1 ( η t , Λ t ) \mathcal{N}^{-1}(\eta_t,\Lambda_t) N−1(ηt,Λt)

令:
![]()
Σ t \mathrm{\Sigma}_t Σt为变量 ξ t \xi_t ξt的协方差矩阵, Λ t \Lambda_t Λt对应为其信息矩阵,值为协方差矩阵 Σ t \mathrm{\Sigma}_t Σt的逆。
协方差矩阵能够很方便的理解变量之间的关系,而信息矩阵能够方便计算概率密度函数。因此关于MLE,MAP构成的最小二乘问题,大部分是使用概率函数(高斯)的负对数函数去除常数项后得到的马氏距离形式,如下所示:
![]()
其中,

使用牛顿法求解迭代公式:
H ∙ δ ξ = − J f T H\ \bullet\ \delta\bm{\xi}=-J_f^T H ∙ δξ=−JfT
其中 H H H为 f ( ξ ) f(\xi) f(ξ)的Hessian矩阵: H = ∂ 2 f ( ξ ) ∂ ξ 2 H=\frac{\partial^2f(\xi)}{{\partial\xi}^2} H=∂ξ2∂2f(ξ), J f 为 f ( ξ ) J_f为f(\xi) Jf为f(ξ)的雅可比矩阵: J f = ∂ f ( ξ ) ∂ ξ J_f=\frac{\partial f(\xi)}{\partial\xi} Jf=∂ξ∂f(ξ)
由1.3信息矩阵和Hessian矩阵内容可知,概率函数的负对数函数的Hessian矩阵对应为高斯状态量正则形式的信息矩阵 Λ \Lambda Λ。
将 r i ( ξ ) \bm{r}_{i}\left(\bm{\xi}\right) ri(ξ)一阶近似展开代入 r i T ( ξ ) Σ i − 1 r i ( ξ ) \bm{r}_{i}^T\left(\bm{\xi}\right){\mathrm{\Sigma}_{i}^{-\mathbf{1}}\bm{r}}_{i}\left(\bm{\xi}\right) riT(ξ)Σi−1ri(ξ)中,求一阶导,得到 J f J_f Jf的近似形式。求二阶导,则可得到 H H H的近似形式:

下降迭代过程变为:

使用联合分布来进一步理解协方差与信息矩阵之间的关系。
1.5 Schur补概念
若 A 非奇异,则有:

令 ∆ A ∆_A ∆A为 A A A的schur补: ∆ A = D − C A − 1 B ∆_A= D-CA^{-1}B ∆A=D−CA−1B

若 D D D非奇异,则: ∆ D = A − B D − 1 C ∆_D=A-BD^{-1}C ∆D=A−BD−1C

1.6 信息矩阵的边缘化
参考论文:《The Humble Gaussian Distribution》。
这篇论文讲述了信息矩阵边缘化的原理。我们在去除一些状态量时,这些状态量往往与其他状态量有联系,通过协方差矩阵,我们直接看出状态量之间的联系,但是信息矩阵却不行,我们在使用马氏距离时都是直接与信息矩阵打交道,而求逆的过程比较复杂,因此需要俩用Schur补计算信息矩阵的逆,得到协方差,利用协方差裁剪状态量。以下通过概率形式,阐述边缘化的意义。更加具体的解释请看上述论文。
对于联合信息分布: p ( a , b ) p(a,b) p(a,b)
设 p ( a , b ) p(a,b) p(a,b)的协方差为:协方差具有对称性:

利用Schur补求得信息矩阵为:
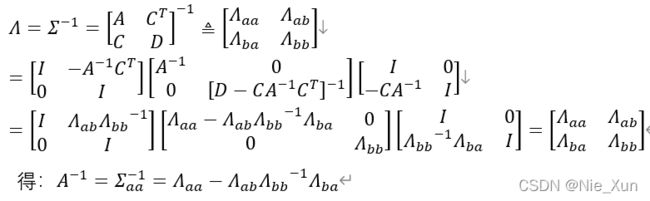
令:
![]()
使用信息矩阵 Λ \mathrm{\Lambda} Λ表示协方差矩阵 Σ \mathrm{\Sigma} Σ:(*3)

联合概率密度函数为:

我们需要从联合分布中去掉与 b b b相关的项,即需要滤除 p ( b ∣ a ) p(b|a) p(b∣a),保留 p ( a ) p(a) p(a)。利用Schur补可以将联合概率分离成 p ( a ) p ( b ∣ a ) p(a)p(b|a) p(a)p(b∣a)的形式。
高斯联合分布普通形式:

高斯联合分布正则形式:

令:

其中 Σ a a − 1 Σ a b = − Λ a b Λ b b − 1 \mathrm{\Sigma}_{aa}^{-1}\mathrm{\Sigma}_{ab}=-\mathrm{\Lambda}_{ab}{\mathrm{\Lambda}_{bb}}^{-1} Σaa−1Σab=−ΛabΛbb−1使用公式**(*3)**可得出。
最终得:
![]()
1.7 贝叶斯后验滤波器
根据贝叶斯条件后验公式:

得到:
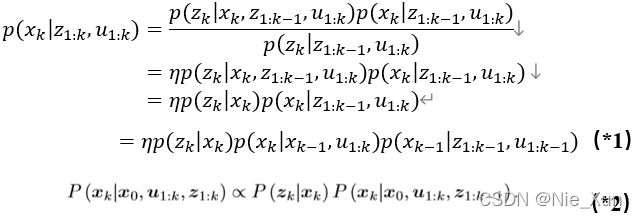
令: p ( x k | z 1 : k , u 1 : k ) ∼ N ( x ^ k , P ^ k ) p\left(x_k\middle| z_{1:k},u_{1:k}\right)\ \sim\ \mathcal{N}({\hat{x}}_k,{\hat{P}}_k) p(xk∣z1:k,u1:k) ∼ N(x^k,P^k),对应 p ( x k − 1 | z 1 : k − 1 , u 1 : k − 1 ) ∼ N ( x ^ k − 1 , P ^ k − 1 ) p\left(x_{k-1}\middle| z_{1:k-1},u_{1:k-1}\right)\ \sim\ \mathcal{N}({\hat{x}}_{k-1},{\hat{P}}_{k-1}) p(xk−1∣z1:k−1,u1:k−1) ∼ N(x^k−1,P^k−1)
其中:
![]()
表示根据t时刻位姿估计得到观测 z k z_k zk的概率。对应观测方程。 z k = C k x k z_k=C_kx_k zk=Ckxk

表示由 k − 1 k-1 k−1时刻位姿估计、给定信号及观测结果得到 x k x_k xk的概率。
![]()
表示由 k − 1 k-1 k−1时刻位姿估计结果得到xk的概率,对应状态传递方程 x k = A k x k − 1 + u k x_k=A_kx_{k-1}+u_k xk=Akxk−1+uk。
![]()
表示由 k − 1 k-1 k−1时刻观测结果及给定信号优化得到 x k − 1 x_{k-1} xk−1的概率, x k − 1 x_{k-1} xk−1与 u k u_k uk无关。
η \eta η为常数:
![]()
贝叶斯概率传递:
EKF及EIF算法皆基于公式 (*1) 作为迭代步骤且假定高斯分布,不同的是EKF使用方差进行状态传递而EIF中使用信息矩阵来进行状态传递且加入了对旧状态的边缘化。
![]()
EKF与EIF均分为两步:1)状态传递 2)状态观测优化

1)时间状态传递: p ( x k ∣ x k − 1 , u 1 : k ) p(x_k|x_{k-1},u_{1:k}) p(xk∣xk−1,u1:k)
在已知上一时刻 k − 1 k-1 k−1状态 x k − 1 x_{k-1} xk−1及当前时刻k的输入量(或者是先验值) u 1 : k u_{1:k} u1:k后,利用状态传递方程 x k = A k x k − 1 + u k x_k=A_kx_{k-1}+u_k xk=Akxk−1+uk推出当前时刻的状态量 x k x_k xk的初始估计,这里设为 x ˉ k {\bar{x}}_k xˉk。
2)状态观测优化
已知当前时刻 k k k状态量的初始估计 x ˉ k {\bar{x}}_k xˉk后,利用当前的观测值对 x ˉ k {\bar{x}}_k xˉk及进行优化,优化后的值记作 x ^ k {\hat{x}}_k x^k。
注意: 在slam问题中,状态量 x k x_k xk包含相机位姿及环境坐标点,但是在时间状态传递时,只有相机的位姿变量会随时间进行传递 ξ k − 1 → ξ k \xi_{k-1}\rightarrow\xi_k ξk−1→ξk,但是环境坐标点 p i p_i pi不随状态方程传递,即 A k A_k Ak中与环境坐标点相关的项为0。
2 概率在线/全局SLAM算法
2.1 卡尔曼滤波(KF)
KF算法思想是:假设位姿估计及观测都是线性的,并且k时刻位姿只与 k − 1 k-1 k−1时刻有关系,且估计噪声假设符合高斯分布,如下:

ω k ∼ N ( 0 , R k ) , v k ∼ N ( 0 , Q k ) \omega_k\sim\mathcal{N}\left(0,R_k\right),\ \ v_k\sim \mathcal{N}\left(0,Q_k\right) ωk∼N(0,Rk), vk∼N(0,Qk)
KF滤波器解算步骤:
1、时间状态传递: p ( x t | z 1 : k − 1 , u 1 : k ) = p ( x k | x k − 1 , u 1 : k ) p ( x k − 1 | z 1 : k − 1 , u 1 : k − 1 ) p\left(x_t\middle|\ z_{1:k-1},u_{1:k}\right)=p\left(x_k\middle|\ x_{k-1},u_{1:k}\right)p\left(x_{k-1}\middle|\ z_{1:k-1},u_{1:k-1}\right) p(xt∣ z1:k−1,u1:k)=p(xk∣ xk−1,u1:k)p(xk−1∣ z1:k−1,u1:k−1)
已知 p ( x k − 1 | z 1 : k − 1 , u 1 : k − 1 ) = N ( x ^ k − 1 , P ^ k − 1 ) p\left(x_{k-1}\middle|\ z_{1:k-1},u_{1:k-1}\right)=\mathcal{N}\left({\hat{x}}_{k-1},{\widehat{\ P}}_{k-1}\right) p(xk−1∣ z1:k−1,u1:k−1)=N(x^k−1, P k−1)
估计通常由前端得到,可以通过图像解析,其他类型轮式里程计或者运动方程得到。其预测估计的状态方程可表示为: P P P表示方差。
![]()
注意:通常预测估计也成为状态时间传递方程,如果变量包含传感器(相机)位置及环境坐标点(即 x k = { ξ k , p 1 , ⋯ , p m } x_k=\left\{\xi_k,p_1,\cdots,p_m\right\} xk={ξk,p1,⋯,pm})在预测估计过程(状态时间传递过程)中,只有相机位置 ξ k \xi_k ξk会随着时间而变化,但环境点不随时间而变化,注意 A k A_k Ak中与环境坐标点相关的部分为0。
根据状态方程可知:

2、状态观测优化: p ( x k | z 1 : k , u 1 : k ) = η p ( z k | x k ) p ( x k | z 1 : k − 1 , u 1 : k ) p\left(x_k\middle| z_{1:k},u_{1:k}\right)=\eta p\left(z_k\middle| x_k\right)p\left(x_k\middle| z_{1:k-1},u_{1:k}\right) p(xk∣z1:k,u1:k)=ηp(zk∣xk)p(xk∣z1:k−1,u1:k)
KF的方法是在原始估计上加上对应权重的观测误差值进行修正,从而得到优化后的参数值,如下:
![]()
关于K的计算则要利用概率模型来计算求解。
由状态传递步骤得到 p ( x t | z 1 : k − 1 , u 1 : k ) = N ( x ˉ k , P ˉ k ) p\left(x_t\middle| z_{1:k-1},u_{1:k}\right)=\ \mathcal{N}\left({\bar{x}}_k,\ {\bar{P}}_k\right) p(xt∣z1:k−1,u1:k)= N(xˉk, Pˉk),且同样定义 p ( x k | z 1 : k , u 1 : k ) = N ( x ^ k , P ^ k ) p\left(x_k\middle| z_{1:k},u_{1:k}\right)=\mathcal{N}\left({\hat{x}}_k,{\widehat{\ P}}_k\right) p(xk∣z1:k,u1:k)=N(x^k, P k)
根据观测方程:
z k = C k x k + v k z_k=C_kx_k+v_k zk=Ckxk+vk
可得: p ( z k | x k ) = N ( C k x k , Q k ) p\left(z_k\middle| x_k\right)=\mathcal{N}\left(C_kx_k,Q_k\right) p(zk∣xk)=N(Ckxk,Qk)
由 p ( x k | z 1 : k , u 1 : k ) = η p ( z k | x k ) p ( x k | z 1 : k − 1 , u 1 : k ) p\left(x_k\middle| z_{1:k},u_{1:k}\right)=\eta p\left(z_k\middle| x_k\right)p\left(x_k\middle| z_{1:k-1},u_{1:k}\right) p(xk∣z1:k,u1:k)=ηp(zk∣xk)p(xk∣z1:k−1,u1:k)整理并取出指数项,常数项直接被忽略,得到:
( x k − x ^ k ) T P ^ k − 1 ( x k − x ^ k ) = ( z k − C k x k ) T Q k − 1 ( z k − C k x k ) + ( x k − x ˉ k ) T P ˉ k − 1 ( x k − x ˉ k ) \left(x_k-{\hat{x}}_k\right)^T{{\widehat{\ P}}_k}^{-1}\left(x_k-{\hat{x}}_k\right)=\left(z_k-C_kx_k\right)^TQ_k^{-1}\left(z_k-C_kx_k\right)+\left(x_k-{\bar{x}}_k\right)^T{{\bar{P}}_k}^{-1}\left(x_k-{\bar{x}}_k\right) (xk−x^k)T P k−1(xk−x^k)=(zk−Ckxk)TQk−1(zk−Ckxk)+(xk−xˉk)TPˉk−1(xk−xˉk)
计算整理得:
P ^ k − 1 = C k T Q k − 1 C k + P ˉ k − 1 {{\widehat{\ P}}_k}^{-1}=C_k^TQ_k^{-1}C_k+{{\bar{P}}_k}^{-1} P k−1=CkTQk−1Ck+Pˉk−1
x ^ k = P ^ k C k T Q k − 1 z k + P ^ k P ˉ k − 1 x ˉ k {\hat{x}}_k={\widehat{\ P}}_kC_k^TQ_k^{-1}z_k+{\widehat{\ P}}_k{{\bar{P}}_k}^{-1}{\bar{x}}_k x^k= P kCkTQk−1zk+ P kPˉk−1xˉk
令:
K = P ^ k C k T Q k − 1 K={\widehat{\ P}}_kC_k^TQ_k^{-1} K= P kCkTQk−1
整理得:
P ^ k = ( I − K C k ) P ˉ k {\widehat{\ P}}_k=\left(I-KC_k\right){\bar{P}}_k P k=(I−KCk)Pˉk
x ^ k = x ˉ k + K ( z k − z k − C k x ˉ k ) {\hat{x}}_k={\bar{x}}_k+K\left(z_k-z_k-C_k{\bar{x}}_k\right) x^k=xˉk+K(zk−zk−Ckxˉk)
整理KF计算流程: ( x ^ k − 1 , P ^ k − 1 , u k , z k ) ({\hat{x}}_{k-1},{\widehat{\ P}}_{k-1},\ u_k,\ z_k) (x^k−1, P k−1, uk, zk)
状态量传递:首先要确立变量的线性状态方程:
![]()
EKF仿真测试:
参考链接:
https://www.cnblogs.com/liuzhenbo/p/12671246.html
https://github.com/liuzhenboo/EKF-2D-SLAM
结果截图:

2.2 扩展卡尔曼滤波器(EKF)
EKF:现实中,运动模型和观测模型通常不是线性的。则权重 K K K得解算变得复杂,因此通过在 k k k时刻,泰勒一阶展开近似,化为时刻线性问题求解。

则预测及优化过程如下表示:
状态传递:
![]()
卡尔曼增益计算:
![]()
状态优化:
![]()
预先估计:由 k − 1 k-1 k−1位姿 ( x k − 1 ) (x_{k-1}) (xk−1)与 k k k刻指令( u k u_k uk)估计k时刻位姿( x k x_k xk)。如下:
![]()
但是,估计存在误差,设误差wk满足高斯分布。
优化估计:获取到 k k k时刻的环境采样信息(图像/点云)后,求出能够产生该采样信息的最大概率的位姿估计,称后验估计,并求出预先估计与后验估计的置信度,分配权重得到优化的位姿估计。
2.3 UKF:TODO
2.4 Information Filter(IF)
IF与KF类似,基于高斯假设,但使用高斯分布的正则形式。IF同KF一样分为状态传递及观测优化两步:时间状态传递与状态观测优化。

1、时间状态传递: p ( x t | z 1 : k − 1 , u 1 : k ) = p ( x k | x k − 1 , u 1 : k ) p ( x k − 1 | z 1 : k − 1 , u 1 : k − 1 ) p\left(x_t\middle| z_{1:k-1},u_{1:k}\right)=p\left(x_k\middle| x_{k-1},u_{1:k}\right)p\left(x_{k-1}\middle| z_{1:k-1},u_{1:k-1}\right) p(xt∣z1:k−1,u1:k)=p(xk∣xk−1,u1:k)p(xk−1∣z1:k−1,u1:k−1)
已知 p ( x k − 1 | z 1 : k − 1 , u 1 : k − 1 ) = N − 1 ( ξ ^ k − 1 , Λ ^ k − 1 ) p\left(x_{k-1}\middle| z_{1:k-1},u_{1:k-1}\right)=\mathcal{N}^{-1}\left({\hat{\bm{\xi}}}_{k-1},{\hat{\mathrm{\Lambda}}}_{k-1}\right) p(xk−1∣z1:k−1,u1:k−1)=N−1(ξ^k−1,Λ^k−1),根据状态传递方程可得k时刻状态初始估计:
![]()
得:
![]()
即:

2、状态观测优化: p ( x k | z 1 : k , t u 1 : k ) = η p ( z k | x k ) p ( x k | z 1 : k − 1 , u 1 : k ) \bm{p}\left(\bm{x}_\bm{k}\middle|\bm{z}_{\mathbf{1}:\bm{k}},\bm t{u}_{\mathbf{1}:\bm{k}}\right)=\bm{\eta p}\left(\bm{z}_\bm{k}\middle|\bm{x}_\bm{k}\right)\bm{p}\left(\bm{x}_\bm{k}\middle|\bm{z}_{\mathbf{1}:\bm{k}-\mathbf{1}},\bm{u}_{\mathbf{1}:\bm{k}}\right) p(xk∣z1:k,tu1:k)=ηp(zk∣xk)p(xk∣z1:k−1,u1:k)
由 p ( x k | z 1 : k , u 1 : k ) = η p ( z k | x k ) p ( x k | z 1 : k − 1 , u 1 : k ) p\left(x_k\middle| z_{1:k},u_{1:k}\right)=\eta p\left(z_k\middle| x_k\right)p\left(x_k\middle| z_{1:k-1},u_{1:k}\right) p(xk∣z1:k,u1:k)=ηp(zk∣xk)p(xk∣z1:k−1,u1:k)整理并取出指数项,常数项直接被忽略,得到:
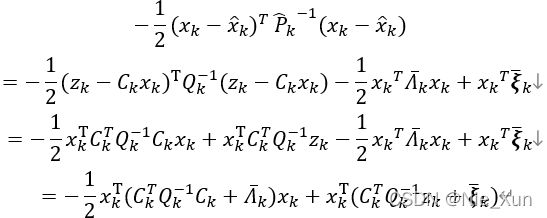
从而可得:
![]()
整理IF的计算流程:( ξ ^ k − 1 , Λ ^ k − 1 , u k , z k {\hat{\bm{\xi}}}_{k-1},{\hat{\mathrm{\Lambda}}}_{k-1},\ u_k,\ z_k ξ^k−1,Λ^k−1, uk, zk)
1、时间状态传递:
![]()
2、观测状态优化:
![]()
2.5 Extended Information Filter (EIF)
过程与EKF类似,同时也使用一阶近似得到状态方程,但是其使用信息矩阵来进行状态传递及更新。同样的如果变量包含传感器(相机)位置及环境坐标点(即 x k = { ξ k , p 1 , ⋯ , p m } x_k=\left\{\xi_k,p_1,\cdots,p_m\right\} xk={ξk,p1,⋯,pm})。在预测估计过程(状态时间传递过程)中,只有相机位置 ξ k \xi_k ξk会随着时间而变化,但环境点不随时间而变化,注意 A k A_k Ak中与环境坐标点相关的部分为0。
定义非线性状态传递方程和观测方程如下:

设:
G k = ∂ g ∂ x k − 1 , H k = ∂ h ∂ x k G_k=\frac{\partial g}{\partial x_{k-1}},H_k=\frac{\partial h}{\partial x_k} Gk=∂xk−1∂g,Hk=∂xk∂h
在计算过程中,由于要计算 g ( u k , x k − 1 ) g(u_k,\ x_{k-1}) g(uk, xk−1)和 z k = h ( x k ) + v k z_k=h(x_k)+v_k zk=h(xk)+vk需要输入状态量 x k − 1 x_{k-1} xk−1,(对应 x ^ k − 1 ) 及 x k ( 对 应 x ˉ k ) {\hat{\bm{x}}}_{k-1})及x_k(对应{\bar{\bm{x}}}_k) x^k−1)及xk(对应xˉk),因此需要计算对应的状态变量值 x ^ k − 1 和 x ˉ k {\hat{\bm{x}}}_{k-1}和{\bar{\bm{x}}}_k x^k−1和xˉk。
EIF本意是利用信息矩阵在计算联合概率分布的优势(其负对数形式可以写成马氏距离的形式),加速求解,但是由于协方差与状态方程的传递方便性 P ˉ k = A k P ^ k − 1 A k T + R k {\bar{P}}_k=A_k{\hat{P}}_{k-1}A_k^T+R_k Pˉk=AkP^k−1AkT+Rk,EKF的实用性更高一些,而EIF使用信息矩阵实现传递,但其间也脱离不了求取协方差,反而多了求逆的过程。另外对于应用到非线性系统,仍需计算 x ^ k − 1 {\hat{\bm{x}}}_{k-1} x^k−1和 x ˉ k {\bar{\bm{x}}}_k xˉk,反而多了计算量。由此有SEIF算法被提出。
EKF求解过程:
1、 时间状态传递:

2、 状态观测优化:
![]()
2.6 粒子滤波器:粒子滤波器是贝叶斯滤波器的实现方式。
建立一群高斯分布的粒子来模拟估计位姿的实际分布。通过观测调整粒子的分布,缩小范围,增大方差。以Rao、ACML等为代表粒子滤波器算法。https://blog.csdn.net/weixin_41469272/article/details/106387716
2.7 图(Graph)优化算法
将状态传递方程及观测方程作为边约束,位姿及环境点(landmark)作为节点构成图模型,如下图所示:

(1) 状态传递构成边约束:

其负对数函数:
![]()
(2) 观测结果构成边约束:

(3) 图优化约束方程
二者负对数函数构成关于各时刻的状态量x_k马氏距离的边约束,构成最小二乘问题:

Tips:
由此可以对比滤波器与图优化的区别:
像EKF,粒子滤波器等优化器是主动式的,在得到新的系统输入或者观测量后,都会对状态进行主动预算和优化。而图优化是建立约束方程,通过求解得到状态估计值。此外,图优化可以用于全局的优化,但是随着时间的推移,状态量(所有帧的位姿及landmark)增多,更新的代价会随着时间推移而增大。而EKF的状态量采用单帧运动及landmark,新的位移产生或者得到新的观测都需要对当前状态量进行更新,即单帧的计算量较大,但随时间的推移增加的计算量相对没有图优化算法明显。图优化模型可用于全局优化,EKF多用于单帧优化。
(4) 图优化求解:
1、使用与IF的解法,使用信息矩阵来求解
先利用所有的输入量 u 1 : t u_{1:t} u1:t得到所有的位姿预估值 ξ 1 : t \xi_{1:t} ξ1:t,利用输入量 u 1 : t u_{1:t} u1:t和观测值组成状态量的信息矩阵,然后利用信息矩阵计算所有状态量 x = { ξ 1 : k , p 1 : m } x=\left\{\xi_{1:k},p_{1:m}\right\} x={ξ1:k,p1:m}。
与IF/KF不同的是,图优化算法,是使用所有状态转移方程和观测方程共同维护一个信息矩阵,并不是每个观测值和每个新的位姿状态都更新。
ξ 1 : k \xi_{1:k} ξ1:k的求解与IF类似。

2、最小二乘问题的优化,多使用下降迭代法:
牛顿法:
H ∙ δ x = − J f T H\ \bullet\ \delta\bm{x}=-J_f^T H ∙ δx=−JfT
高斯牛顿法近似:
∑ i J i T Σ i − 1 J i ∙ δ x = ∑ i J i T Σ i − 1 r i \sum_{i}{J_i^T\mathrm{\Sigma}_\bm{i}^{-\mathbf{1}}J_i}\ \bullet\ \delta\bm{x}=\sum_{i}{J_i^T\mathrm{\Sigma}_\bm{i}^{-\mathbf{1}}\bm{r}_\bm{i}} i∑JiTΣi−1Ji ∙ δx=i∑JiTΣi−1ri
最后得到的Hessian矩阵 H = ∑ i J i T Σ i − 1 J i H=\sum_{i}{J_i^T\mathrm{\Sigma}_\bm{i}^{-\mathbf{1}}J_i} H=∑iJiTΣi−1Ji的形式:

此时,可以利用Schur补来简化求解步骤。
将 H H H矩阵分块:

使用原始迭代 H ∆ x = g ( g = − J T = 2 J r T r ) H∆x=g(g=-J^T=2J_rT_r) H∆x=g(g=−JT=2JrTr)方程变为:

这样需求解 ∆ x ∆x ∆x会产生对H的求逆过程,因此计算过程较为复杂,可以通过Schur补的方式将计算分块,简化运算步骤。此外,可以用Huber过滤外点。
- 利用Schur补,简化求逆过程。
由于H的对称性及Schur补性质,上式可整理成:

从而,可以利用:
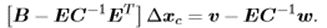
得到 ∆ x c ∆x_c ∆xc,带回方程,从而得到 ∆ x p ∆xp ∆xp,继而得到:

将 H H H求逆,转变为 C C C求逆,减少了很大的计算量。 - 利用鲁函数,减少噪声数据对结果的影响。
如最常用的 Huber 核:

当误差 e e e 大于某个阈值 δ δ δ 后,函数增长由二次形式变成了一次形式,相当 于限制了梯度的最大值。同时,Huber 核函数又是光滑的,可以很方便地求导。如下图所示。

- 边缘化(marginalization)变量
当遇到曾经遇到过的landmark时,可以使用边缘化(marginalization)先去掉信息矩阵中landmark项,在将新的观测结果添加到信息矩阵中。另外对于一些观测比较少的landmark变量及较久远的姿态量都可以通过边缘化来削减信息矩阵的维度。
边缘化的优化步骤:
形如的信息矩阵,如下图所示,去掉 ξ 1 \xi_1 ξ1,将信息矩阵分为四块, β \beta β表示与 ξ 1 \xi_1 ξ1有关的信息量,通过矩阵块之间的运算去掉 ξ 1 \xi_1 ξ1的信息。在去掉 ξ 1 \xi_1 ξ1后,剩余矩阵不再稀疏。详细推导见1…6信息矩阵边缘化

2.8 SEIF算法
SEIF是一种基于EIF改进的算法,可以利用信息矩阵创建便约束来求解状态量。SEIF是一种在线估计算法,其维护的状态变量与EKF相同,只维护当前帧的相机位姿及环境点,如下:
x k = { ξ k , p 1 , ⋯ , p m } x_k=\left\{\xi_k,p_1,\cdots,p_m\right\} xk={ξk,p1,⋯,pm}
SEIF步骤:运动更新、测量更新、稀疏化和状态估计。
- 测量更新:

信息矩阵只建立与当前位姿状态相关的环境点(landmark),这样的点成为(active points) - 运动更新:
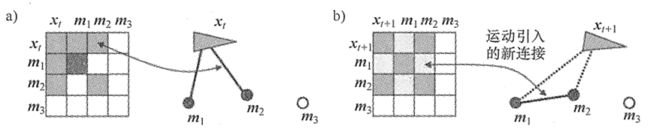
Marg掉上一姿态信息,加入新的运动状态及测量信息,此时由于边缘化掉上一时刻的位姿信息,会在信息矩阵中引入环境点(landmark)之间的联系。 - 稀疏化

直接去掉信息矩阵中与当前位姿无关的环境点(landmark)的相关性,从而维持信息矩阵的稀疏性。 - 状态估计
同样以之前与GraphSLAM的方法类似求解状态量。
此外由于SEIF直接将信息矩阵中非与当前位姿相关的环境路标点的联系去掉,因此带来一些信息的丢失,因此SSEIF等算法被提出。
3 非线性优化
现代算法中很多场景需要计算非线性优化问题,比如图优化算法,以及DL问题,大部分都是使用最小二乘法问题。目前采用逐步迭代法,来一步步优化求解非线性优化的解决方法。目前常用的方法:最速下降法,牛顿法,高斯牛顿法及LM法等。
首先构造最小二乘问题:

通常,如果函数比较简单,我们求导数就可以完成,但是,通常 r ( x ) r\left(x\right) r(x)是多为的,复杂的,而且x是具有区域限制的。因此实际工程中,需要使用迭代法,逐步迭代优化,来步步逼近目标函数最小。如: r ( x ) r\left(x\right) r(x)是多维的,且定义域有限制,这样求解会非常困难。
3.1 梯度矩阵Jacobians矩阵及Hessian矩阵
参考链接:https://blog.csdn.net/tina_ttl/article/details/51202566
梯度(gradient)矩阵, 由一维函数 f ( x ) f\left(x\right) f(x)对自变量各维度的偏导数组成的向量。

梯度向量和Jacobi矩阵的关系:梯度向量用于一维函数,当目标函数为标量函数时,Jacobi矩阵等于梯度向量的转置。
考虑多维函数最小化: m i n f ( x ) , x ∈ R n , f ( x ) ∈ R m min\ f(x),\ \ x\in\mathbb{R}^n,f(x)\in\mathbb{R}^m min f(x), x∈Rn,f(x)∈Rm
将函数 f ( x + ∆ x ) f(x+∆x) f(x+∆x)关于泰勒展开:
f ( x + ∆ x ) = f ( x ) + J T ( x ) ∆ x + 1 2 ∆ x T H ∆ x f(x+∆x)=f(x)+J^T(x)∆x+\frac12∆x^TH∆x f(x+∆x)=f(x)+JT(x)∆x+21∆xTH∆x
其中, J ( x ) J({x}) J(x)成为Jacobians矩阵,如下:

H为hessian矩阵,如下:

迭代法具体步骤:
- 设定 x x x初始值 x 0 x_0 x0;
- 对于第 k k k次迭代,确定迭代下降方向 ∆ x k ∆x_k ∆xk,求解 f ( x k + α k ∆ x k ) f(x_k+α_k∆x_k) f(xk+αk∆xk)得下降步长 α k \alpha_k αk。
- f ( x k + α k ∆ x k ) f(x_k+α_k∆x_k) f(xk+αk∆xk)足够小,停止迭代。 ∣ ∣ f ( x k + α k ∆ x k ) ∣ ∣ 2 2 ||f(x_k+α_k∆x_k)||^2_2 ∣∣f(xk+αk∆xk)∣∣22
- 否则,令 x k + 1 = x k + α k ∆ x k {x_{k+1}=x}_k+\alpha_k∆x_k xk+1=xk+αk∆xk,继续迭代返回2)。
3.2 最速下降法
3.3 牛顿法:考虑函数向量的二阶导数
将函迭代函数二阶泰勒展开:
f ( x + ∆ x ) = f ( x ) + J T ( x ) ∆ x + 1 2 ∆ x T H ∆ x f(x+∆x)=f(x)+J^T(x)∆x+\frac12∆x^TH∆x f(x+∆x)=f(x)+JT(x)∆x+21∆xTH∆x
求等式右侧二阶展开近似展开关于 ∆ x ∆x ∆x的导数=0,求得:迭代方向 ∆ x ∆x ∆x
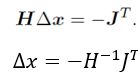
牛顿法相比最速下降法,是考虑了二阶展开式进来,使得函数近似更加接近。


3.4 高斯牛顿法(GN)
由于牛顿法,Hessian阵得逆求解运算量大,或者存在奇异可能。因此高斯牛顿法用来弥补牛顿法得不足。主要用于求最小二乘问题。
我们研究如下形式的非线性最小二乘问题:

牛顿迭代公式:


将 r ( x ) r\left(x\right) r(x)泰勒一阶展开,并其泰勒展开相乘,得到近似的 r 2 ( x ) r^2\left(x\right) r2(x):

高斯牛顿法使用其他矩阵计算代替海森矩阵。

即: J T = 2 J r T r , H ≈ 2 J r T J r J^T=2{J_r}^Tr,H≈2{J_r}^TJ_r JT=2JrTr,H≈2JrTJr
证明就是将 r ( x ) r(x) r(x)方程的1阶泰勒展开带入到 f ( x ) = r 2 ( x ) f(x)=r^2(x) f(x)=r2(x)中,得到的二阶项的乘数就约等于 H H H。这样能够简化 H H H阵的计算,且增加 H H H正定的可能性。
则迭代公式为:

3.5 LM(Levenberg-Marquadt)
L-M法其实是修正牛顿法,因为hessian矩阵可能是非正定的,那么迭代的方向就不是下降方向。除了GN法,另外LM法修正hessian矩阵来保证下降方向:
G = H + μ I G=H+\mu I G=H+μI,从而保证矩阵正定, G G G的特征值: λ i + μ \lambda_i+\mu λi+μ。
迭代公式为:
![]()
当 μ \mu μ很小时,补偿项 μ I \mu I μI作用很小,迭代接近牛顿法。
当 μ \mu μ很大时, H H H的作用比例很小, ( H + μ I ) ∇ f = μ ∗ ∇ f \left(H+\mu I\right)\nabla f=\mu\ast\nabla f (H+μI)∇f=μ∗∇f,相当于迭代接近最速下降法。
3.6 信赖域法
信赖区域方法(Trust Region),信赖域方法的思路有所不同。在信赖域方法的每次迭代中,先确定一个信赖域半径,然后在该半径内计算目标函数的二阶近似的极小值。如果该极小值使得目标函数取得了充分的下降,则进入下一个迭代,并扩大信赖域半径,如果该极小值不能令目标函数取得充分的下降,则说明当前信赖域区域内的二阶近似不够可靠,需要缩小信赖域半径,重新计算极小值。如此迭代下去,直到满足收敛所需的条件。
参考链接https://zhuanlan.zhihu.com/p/99392484
考虑近似程度的描述:

若 ρ \rho ρ太小,则减小近似范围
若 ρ \rho ρ太大,则增加近似范围
4 解算工具介绍(ceres/g2o)
Ceres 相对g2o的配置要简单一些,ceres需将残差约束添加到定义的问题中,然后配置求解器,就可以求解问题;g2o是基于图优化思路,需要添加点和边的约束,然后配置求解器,求解问题。
4.1 Ceres
Ceres solver 是谷歌开发的一款用于非线性优化的库,在谷歌的开源激光雷达slam项目cartographer中被大量使用。Ceres官网上的文档非常详细地介绍了其具体使用方法,相比于另外一个在slam中被广泛使用的图优化库G2O,ceres的文档可谓相当丰富详细。
官网地址:http://www.ceres-solver.org/
参考链接:https://www.jianshu.com/p/e5b03cf22c80
使用Ceres求解非线性优化问题,一共分为三个部分:
1、第一部分:构建cost fuction结构体,即代价函数结构体。使用仿函数(functor),做法是定义一个cost function的结构体,在结构体内重载()运算符,这样可以使该结构体cost fuction的一个实例具有函数的性质。重载()运算符时,定义代价函数,即使cost fuction(value)类似函数一样实现代价的计算。
2、第二部分:通过代价函数构建待求解的优化问题ceres::Problem。将所有约束(CostFunction)添加到(AddResidualBlock)到problem中。
3、第三部分:配置求解器参数并求解问题,这个步骤就是设置方程怎么求解、求解过程是否输出等,然后调用一下Solve方法。
#include4.2 G2o
G2o(General Graphic Optimization,G2O)是主要在 SLAM 领域广为使用的优化库。它是一个基于图优化的库。图优化是一种将非线性优化与图论结合起来的理论。将点(Vertex)约束和边(Edge)约束添加到求解器求解问题。在slam中点约束(Vertex)是相机在各时刻的位置及环境点的位置,而边约束(Edge)则是环境点在对应时刻被相机观测到的结果。
G2o图优化步骤:
1、定义顶点和边的类型;
1)顶点类:Vertex
继承:g2o::BaseVertex
模板参数:优化变量维度和数据类型。
class pointVertex: public g2o::BaseVertex<3, Eigen::Vector3d>
主要关注实现函数:
virtual void setToOriginImpl():重置初始评估值。
virtual void oplusImpl( const double* update ) // 更新评估值
15 // 曲线模型的顶点,模板参数:优化变量维度和数据类型
16 class CurveFittingVertex: public g2o::BaseVertex<3, Eigen::Vector3d>
17 {
18 public:
19 EIGEN_MAKE_ALIGNED_OPERATOR_NEW
20 virtual void setToOriginImpl() // 重置
21 {
22 _estimate << 0,0,0;
23 }
24
25 virtual void oplusImpl( const double* update ) // 更新
26 {
27 _estimate += Eigen::Vector3d(update);
28 }
29 // 存盘和读盘:留空
30 virtual bool read( istream& in ) {}
31 virtual bool write( ostream& out ) const {}
32 };
2)约束边类:Edge
继承:g2o::BaseUnaryEdge
模板参数:观测值维度,类型,连接顶点类型
class CurveFittingEdge: public g2o::BaseUnaryEdge<1,double,CurveFittingVertex>
主要关注实现函数:
CurveFittingEdge( double x ): BaseUnaryEdge(), _x(x) {}:构造函数
void computeError():计算曲线模型误差
34 // 误差模型 模板参数:观测值维度,类型,连接顶点类型
35 class CurveFittingEdge: public g2o::BaseUnaryEdge<1,double,CurveFittingVertex>
36 {
37 public:
38 EIGEN_MAKE_ALIGNED_OPERATOR_NEW
39 CurveFittingEdge( double x ): BaseUnaryEdge(), _x(x) {}
40 // 计算曲线模型误差
41 void computeError()
42 {
43 const CurveFittingVertex* v = static_cast<const CurveFittingVertex*> (_vertices[0]);
44 const Eigen::Vector3d abc = v->estimate();
45 _error(0,0) = _measurement - std::exp( abc(0,0)*_x*_x + abc(1,0)*_x + abc(2,0) ) ;
46 }
47 virtual bool read( istream& in ) {}
48 virtual bool write( ostream& out ) const {}
49 public:
50 double _x; // x 值, y 值为 _measurement
51 };
2、构建图
1)创建solver,并设置solver参数(求解器及优化方法等):
2)创建optimizer。
74 // 构建图优化,先设定g2o
75 typedef g2o::BlockSolver< g2o::BlockSolverTraits<3,1> > Block; // 每个误差项优化变量维度为3,误差值维度为1
76 Block::LinearSolverType* linearSolver = new g2o::LinearSolverDense<Block::PoseMatrixType>(); // 线性方程求解器
77 Block* solver_ptr = new Block( unique_ptr<Block::LinearSolverType>(linearSolver) ); // 矩阵块求解器
78 // 梯度下降方法,从GN, LM, DogLeg 中选
79 g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg( unique_ptr<Block>(solver_ptr) );
80 // g2o::OptimizationAlgorithmGaussNewton* solver = new g2o::OptimizationAlgorithmGaussNewton( solver_ptr );
81 // g2o::OptimizationAlgorithmDogleg* solver = new g2o::OptimizationAlgorithmDogleg( solver_ptr );
82 g2o::SparseOptimizer optimizer; // 图模型
83 optimizer.setAlgorithm( solver ); // 设置求解器
84 optimizer.setVerbose( true ); // 打开调试输出
3)添加节点到图
86 // 往图中增加顶点
87 CurveFittingVertex* v = new CurveFittingVertex();
88 v->setEstimate( Eigen::Vector3d(0,0,0) );
89 v->setId(0);
90 optimizer.addVertex( v );
91
4)添加约束边到图
95 CurveFittingEdge* edge = new CurveFittingEdge( x_data[i] );
96 edge->setId(i);
97 edge->setVertex( 0, v ); // 设置连接的顶点
98 edge->setMeasurement( y_data[i] ); // 观测数值
99 edge->setInformation( Eigen::Matrix<double,1,1>::Identity()*1/(w_sigma*w_sigma) ); // 信息矩阵:协方差矩阵之逆
100 optimizer.addEdge( edge );
3、Optimizer初始化及优化步设置
106 optimizer.initializeOptimization();
107 optimizer.optimize(100);
参考链接:https://blog.csdn.net/wphkadn/article/details/90317006?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task
4.3 GTSAM
参考链接:
https://gtsam.org/tutorials/intro.html#listing_OdometryOptimize
https://blog.csdn.net/weixin_41394379/article/details/87967446
https://github.com/borglab/gtsam.git
Gtsam能够完成增量式优化,gtsam的使用与g2o的构建思路类似,都是创建graph添加需要计算优化的节点(Nodes),以及已知的观测约束(Factor),然后使用calculateEstimate()进行优化计算。大致步骤如下:
1)首先要选择测量变量的约束类型(Factor),并添加对应头文件,
声明Graph类型,isam2,nodes等
xxxFactorGraph graph;
std::unique_ptr<ISAM2> isam;
Values newNodes; 用于存放需要计算的变量
//Values optimizedNodes;用于存放优化后的变量值
//设置isam参数:
ISAM2Params parameters;
parameters.optimizationParams = ISAM2DoglegParams();
parameters.factorization = ISAM2Params::QR;
//parameters.relinearizeThreshold = 0.01;
//parameters.relinearizeSkip = 5;
isam.reset(new ISAM2(parameters));
Gtsam提供了很多factor:
Slam中常用的有:
双目匹配约束:GenericStereoFactor
图像3D-2D投影约束:GenericProjectionFactor
3D-3D点云约束:ExpressionFactor
等。。。
2)定义变量初始值以及观测的概率模型
noiseModel::Diagonal::shared_ptr xxxNoise = noiseModel::Diagonal::Sigmas((Vector(3)<<0.0,0.0,0.0).finished());
…
3)添加初始化节点
graph.addPrior(xxx);
4)添加待计算的节点变量,每个节点对应各自单独的Symbol。
Nodes.insert(Symbol('x', pose_id), curCamPose);
Nodes.insert<Point3>(Symbol('l', landmark_id), worldPoint);
5)添加观测Factor约束:
两种添加方式:
1、graph.addxxxFactor();
2、graph.emplace_shared<xxxFactor>();
6)计算变量
isam->update(gtSAMgraph, newNodes);
optimizedNodes = isam->calculateEstimate();
//根据节点symble提取变量值
curCamPose = optimizedNodes.at<Pose3>(Symbol('x', pose_id));
5 参考
[1] 《高翔十四讲》
[2] 《Probabilistic Robotics》
[3] 《最优化理论及算法_陈宝林》
[4] Walter M R , Eustice R M , Leonard J J . Exactly Sparse Extended Information Filters for Feature-based SLAM[J]. The International Journal of Robotics Research, 2007, 26(4):335-359.
[5] Mackay D J C . The Humble Gaussian Distribution. 2006.


