DLT-06-多元分类

本文是**深度学习入门（deep learning tutorial, DLT）**系列的第五篇文章，主要介绍一下多元分类。想要学习深度学习或者想要了解机器学习的同学可以关注公众号GeodataAnalysis，我会逐步更新这一系列的文章。

1 多元分类模型表示

多元分类也被叫做“一对多”或“一对余”分类，其本质是依然是二元分类。只不过是多个类中的一个类标记为正向类（$y=1$），然后将其他所有类都标记为负向类，这个模型记作$h_{\theta }^{\left(1\right)}\left(x\right)$。接着，类似地第我们选择另一个类标记为正向类（$y=2$），再将其它类都标记为负向类，将这个模型记作 $h_{\theta }^{\left(2\right)}\left(x\right)$,依此类推。

最后我们得到一系列的模型简记为： $h_{\theta }^{\left(i\right)}\left(x\right)=p\left(y=i|x;\theta \right)$其中：$i=\left(1,2,\mathrm{3....}k\right)$

在我们需要做预测时，我们将所有的分类机都运行一遍，然后对每一个输入变量，都选择最高可能性的输出变量。

总之，如果你已经学会了二元分类，那么我们已经把要做的做完了，现在要做的就是训练这个逻辑回归分类器：$h_{\theta }^{\left(i\right)}\left(x\right)$， 其中 $i$ 对应每一个可能的 $y=i$，最后，为了做出预测，我们给出输入一个新的 $x$ 值，用这个做预测。我们要做的就是在我们三个分类器里面输入 $x$，然后我们选择一个让 $h_{\theta }^{\left(i\right)}\left(x\right)$ 最大的$i$，即$\underset{i}{\max }{h}_{\theta }^{\left(i\right)}\left(x\right)$。

2 对二元分类模型进行封装

通过前面的解释我们已经知道，多元分类模型本质上相当远多个二元分类模型的集合。因此，我们这里先对上一章的二元分类模型进行封装，以便后续的使用。封装方法类似于第三章多元线性回归的模型封装，区别仅在于初始化实例时增加一个参数，可以对数据做一些变换，代码如下：

class LogicRe():

	def __init__(self, x, y, times=1):
		self.y = y
		self.x = x
		self.times = times
		for i in range(2, times+1):
		    self.x = np.vstack((self.x, x**i))
		self.input_shape = self.x.shape
		self.parameters = np.random.rand(self.input_shape[0]+1)

	# 省略其他函数，可参考第三章多元线性回归的代码

    def predict(self, input_x):
        x = input_x.copy()
        for i in range(2, self.times+1):
            x = np.vstack((x, input_x**i))
        x = self._normalization(x, self.normalization)
        x = np.vstack((np.ones(self.input_shape[1]), x))
        p = self.hypothesis_fun(x, self.parameters)
        return p

3 鸾尾花数据集

from sklearn import datasets

iris = datasets.load_iris()

x = iris.data.T
y = iris.target
x.shape, y.shape, np.unique(y)

((4, 150), (150,), array([0, 1, 2]))

4 模型训练及预测

models = []
for i in np.unique(y):
	x2, y2 = x.copy(), y.copy()
	y2[y==i] = 1
	y2[y!=i] = 0
	model = LogicRe(x2, y2, times=3)
	model.fit(epoch_size=1000, batch_size=100, 
			train_step=100, learning_rate=0.1, 
			normalization='feature')
	models.append(model)

predict_ys = []
for model in models:
    predict_y = model.predict(x)
    predict_ys.append(predict_y)
predict_y = np.array(predict_ys)
predict_y = np.argmax(predict_y, axis=0)

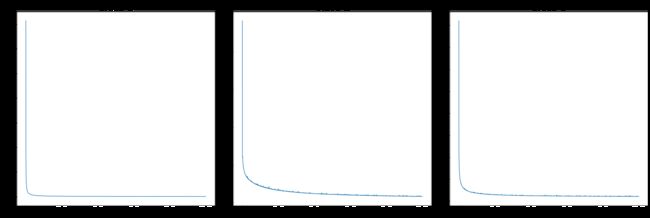
fig, axs = plt.subplots(1, 3, figsize=(27, 9), constrained_layout=True)

for i, (model, ax) in enumerate(zip(models, axs)):
	ax.plot(model.loss[:])
	ax.set_xlabel('Iteration number')
	ax.set_ylabel('Loss')
	ax.set_title('Class {}'.format(i+1), fontdict={'size': 30})
plt.show()

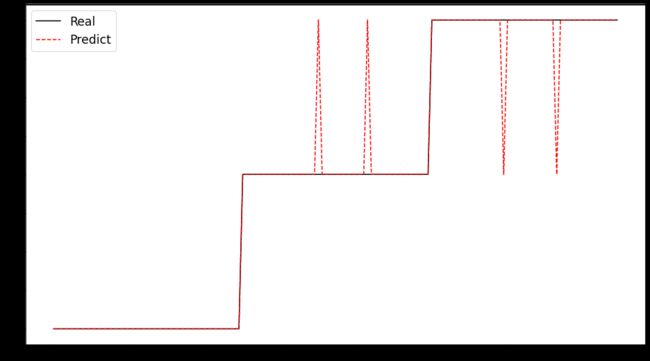
预测结果可视化

fig, ax = plt.subplots(1, 1, figsize=(16, 9))

ax.plot(y, 'k-', label='Real')
ax.plot(predict_y, 'r--', label='Predict')
plt.legend(fontsize='xx-large')
plt.show();