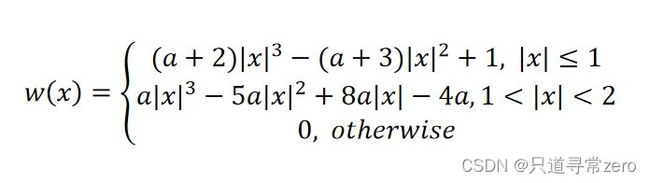数字图像处理学习之路（三）：你还不会图像的放大缩小吗？使用最近邻插值、双线性插值以及双三次插值方式实现图像放缩

简介

数字图像是由一个个像素点组成的，要实现图像的放大缩小就是将图像的像素值映射到一块新的区域，从而实现图像的放缩。比如一块3x3的区域放大到5x5，使用最近邻插值如下图所示：

（注：这里的颜色和像素值无关，只是为了更好的反映图像间像素值的映射关系。）

一、最近邻插值

最近邻插值顾名思义就是选择邻近的像素点的值来作为新的位置的像素值，通过四舍五入即可实现。

最近邻插值的步骤如下：

1.计算放缩后的图像当前点(i,j)在原图像中对应的位置(srcX,srcY): (src表示输入图像，dst表示输出图像)。
$$srcX=i\ast （srcImage.rows/dstImage.rows）$$

$$srcY=j\ast (srcImage.cols/dstImage.cols)$$

2.由第一步计算出来的位置是浮点数，通过四舍五入得到整数位置。

3.在原图像中找到(srcX,srcY)点的像素值并赋值给当前图像。
$$dstImage(i,j)=srcImage(srcX,srcY)$$
完整实现代码如下：

	for (int i = 0; i < dstImage.rows; i++) {
		for (int j = 0; j < dstImage.cols; j++)
		{
            //这里加上0.5是为了实现四舍五入
			srcX = i * (srcImage.rows * 1.0 / dstImage.rows) + 0.5;
			srcY = j * (srcImage.cols * 1.0 / dstImage.cols) + 0.5;
            //防溢出
			if (srcX >= srcImage.rows)
				srcX = srcImage.rows - 1;
			if (srcY >= srcImage.cols)
				srcY = srcImage.cols - 1;
			dstImage.at<uchar>(i, j) = srcImage.at<uchar>(srcX, srcY);
		}
	}

二、双线性插值

本文在开头已经说明图像的放缩主要是靠原图像的像素值通过某种映射关系填充到新的图像中，双线性插值就是通过计算像素点(srcX,srcY)周围4个点的双线性插值得到周围像素的加权平均值，然后将其填充到当前位置(i,j)。

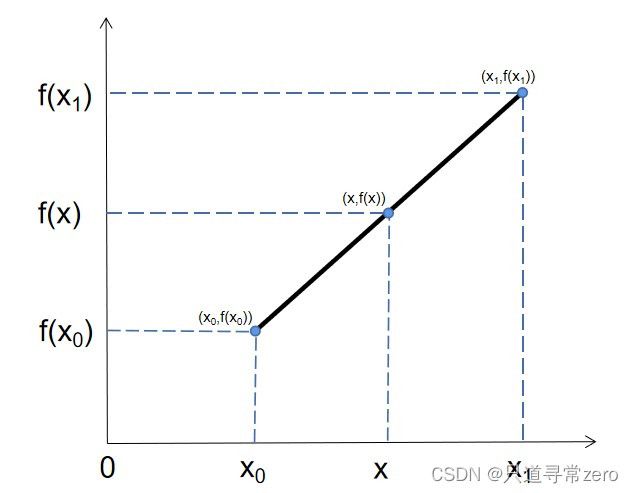
双线性插值：先在X方向进行两次单线性插值，然后再对Y方向做一次单线性插值。

单线性插值方法介绍：

由公式
$$\frac{f(x)-f(x_0)}{x-x_0}=\frac{f(x_1)-f(x_0)}{x_1-x_0}$$
可得
$$f(x)=\frac{x-x_0}{x_1-x_0}f(x_1)+\frac{x_1-x}{x_1-x_0}f(x_0)$$
由此可见，x处的函数值可由线上的两点加权计算得到。

双线性插值方法介绍：

先在X方向进行两次线性插值得到R1,R2的值
$$R1=\frac{x_2-srcX}{x_2-x_1}{Q}_{11}+\frac{srcX-x_1}{x_2-x_1}{Q}_{21},R2=\frac{x_2-srcX}{x_2-x_1}{Q}_{12}+\frac{srcX-x_1}{x_2-x_1}{Q}_{22}$$
再对计算得到的R1，R2在Y方向上进行线性插值得到最终的P值
$$P=\frac{y_2-srcY}{y_2-y_1}{R}_1+\frac{srcY-y_1}{y_2-y_1}{R}_2,$$
完整实现代码如下：

	for (int i = 0; i < dstImage.rows; i++) {
		for (int j = 0; j < dstImage.cols; j++)
		{
			//找到原始点的位置 ，选取最近的四个点的像素值进行加权计算然后赋值
			srcX = i * (srcImage.rows * 1.0 / dstImage.rows);
			srcY = j * (srcImage.cols * 1.0 / dstImage.cols);
			x1 = srcX;
			x2 = srcX + 1 > srcImage.rows - 1 ? srcX - 1 : srcX + 1;//防溢出处理
			y1 = srcY;
			y2 = srcY + 1 > srcImage.cols - 1 ? srcY - 1 : srcY + 1;
			Q11 = srcImage.at<uchar>(x1, y1);
			Q12 = srcImage.at<uchar>(x1, y2);
			Q21 = srcImage.at<uchar>(x2, y1);
			Q22 = srcImage.at<uchar>(x2, y2);
			R1 = (x2 - srcX) / (x2 - x1) * Q11 + (srcX - x1) / (x2 - x1) * Q21;
			R2 = (x2 - srcX) / (x2 - x1) * Q12 + (srcX - x1) / (x2 - x1) * Q22;
			P = (y2 - srcY) / (y2 - y1) * R1 + (srcY - y1) / (y2 - y1) * R2;
            //saturate_cast(P) OpenCV中的函数可以防溢出
			dstImage.at<uchar>(i, j) = saturate_cast<uchar>(P);
		}
	}

三、双三次插值

双线性插值计算像素点(srcX,srcY)周围4个点的像素值的加权平均值，而双三次插值计算的是周围16个点的像素值的加权平均值。

如图所示，(ai,bi)代表的是周围16个点的坐标位置，Qi表示该点的像素值，w1[i]计算的是X方向上的权重，w2[i]计算的是Y方向上的权重，最终每个点的权重都由w1与w2中的值相乘得到。通常使用BiCubic公式来进行权重的计算（BiCubic插值 ）。

a的值通常取-0.5，这里的|x|表示的是距离，比如计算(a1,b1)点对应的权重，X方向上用|a1-srcX|带入公式计算，Y方向上用|b1-srcY|带入公式计算。

综上，最终的像素值P的计算公式如下：
$$P=\left[\begin{array}{cccc}w1[0]& w1[1]& w1[2]& w1[3]\end{array}\right]\left[\begin{array}{cccc}Q1& Q2& Q3& Q4\\ Q5& Q6& Q7& Q8\\ Q9& Q10& Q11& Q12\\ Q13& Q14& Q15& Q16\end{array}\right]{\left[\begin{array}{cccc}w2[0]& w2[1]& w2[2]& w2[3]\end{array}\right]}^T$$
完整实现代码如下：

void ReSize(Mat srcImage)
{
    Mat dstImage = Mat((srcImage.size()) * 4, srcImage.type());
    double srcX = 0;
	double srcY = 0;
	int a1=0, a2=0, a3=0, a4=0;
	int b1=0, b2=0, b3=0, b4=0;
	double w1[4],w2[4];//对应x,y的权重
	int P=0;
	double sum = 0;
	for (int i = 0; i < dstImage.rows; i++) {
		for (int j = 0; j < dstImage.cols; j++)
		{
			//找到原始点的位置 ，选取最近的16个点的像素值进行加权计算然后赋值
			srcX = i * (srcImage.rows * 1.0 / dstImage.rows);
			srcY = j * (srcImage.cols * 1.0 / dstImage.cols);
			a1 = (srcX - 1) < 0 ? (srcX + 1) : (srcX - 1); //用三元表达式实现边界处理，镜像像素值
			a2 = srcX < 0 ? 0 : srcX;
			a3 = (srcX + 1) > srcImage.rows - 1 ? (srcX - 1) : (srcX + 1);
			a4 = (srcX + 2) > srcImage.rows - 1 ? (srcX - 2) : (srcX + 2);
			b1 = (srcY - 1) < 0 ? (srcY + 1) : (srcY - 1);
			b2 = srcY;
			b3 = (srcY + 1) > srcImage.cols - 1 ? (srcY - 1) : (srcY + 1);
			b4 = (srcY + 2) > srcImage.cols - 1 ? (srcY - 2) : (srcY + 2);
			w1[0] = countW(-0.5, srcX - a1);
			w1[1] = countW(-0.5, srcX - a2);
			w1[2] = countW(-0.5, srcX - a3);
			w1[3] = countW(-0.5, srcX - a4);
			w2[0] = countW(-0.5, srcY - b1);
			w2[1] = countW(-0.5, srcY - b2);
			w2[2] = countW(-0.5, srcY - b3);
			w2[3] = countW(-0.5, srcY - b4);
            //注意要将权重归一化
			sum = w1[0] * w2[0] + w1[0] * w2[1] + w1[0] * w2[2] + w1[0] * w2[3]
				+ w1[1] * w2[0] + w1[1] * w2[1] + w1[1] * w2[2] + w1[1] * w2[3]
				+ w1[2] * w2[0] + w1[2] * w2[1] + w1[2] * w2[2] + w1[2] * w2[3]
				+ w1[3] * w2[0] + w1[3] * w2[1] + w1[3] * w2[2] + w1[3] * w2[3];
			P = srcImage.at<uchar>(a1, b1) * w1[0] * w2[0] / sum + srcImage.at<uchar>(a1, b2) * w1[0] * w2[1] / sum +
				srcImage.at<uchar>(a1, b3) * w1[0] * w2[2] / sum + srcImage.at<uchar>(a1, b4) * w1[0] * w2[3] / sum +
				srcImage.at<uchar>(a2, b1) * w1[1] * w2[0] / sum + srcImage.at<uchar>(a2, b2) * w1[1] * w2[1] / sum +
				srcImage.at<uchar>(a2, b3) * w1[1] * w2[2] / sum + srcImage.at<uchar>(a2, b4) * w1[1] * w2[3] / sum +
				srcImage.at<uchar>(a3, b1) * w1[2] * w2[0] / sum + srcImage.at<uchar>(a3, b2) * w1[2] * w2[1] / sum +
				srcImage.at<uchar>(a3, b3) * w1[2] * w2[2] / sum + srcImage.at<uchar>(a2, b4) * w1[2] * w2[3] / sum +
				srcImage.at<uchar>(a4, b1) * w1[3] * w2[0] / sum + srcImage.at<uchar>(a4, b2) * w1[3] * w2[1] / sum +
				srcImage.at<uchar>(a4, b3) * w1[3] * w2[2] / sum + srcImage.at<uchar>(a4, b4) * w1[3] * w2[3] / sum;
			dstImage.at<uchar>(i, j) = saturate_cast<uchar>(P);
		}
	}
}
double countW(double a ,double x) {
	x = abs(x);//取绝对值
	if (x <= 1)
		return (a + 2) * pow(x,3)- ( a + 3 ) * pow(x,2) + 1;
	else if (x > 1 && x < 2)
		return a * pow(x,3) - 5 * a * pow(x,2) + 8 * a * x - 4 * a;
	else
		return 0;
}

四、关于边界像素点的特殊处理

如果计算出来的(srcX,srcY)是位于边界上的点，那么周围就会出现空值，对应的位置选择对称点的像素值来填充，如图所示，相应的位置已填充上对应的像素值。

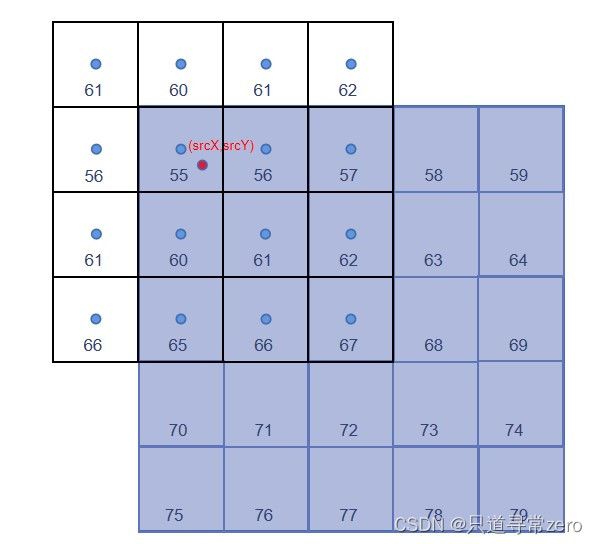
			 //用三元表达式实现边界处理 若(srcX - 1)<0则取它关于当前点的对称位置(srcX + 1)，否则则取(srcX - 1)
			a1 = (srcX - 1) < 0 ? (srcX + 1) : (srcX - 1);

五、三种插值方式的效果对比

使用最近邻插值放大图片

使用双线性插值放大图片

使用双三次插值放大图片

可以看到使用最近邻插值放大的图片出现了马赛克，后两种插值的放大效果明显要更好。这是因为后两种插值方式对周围的像素值进行了加权平均，使得总体图像更平滑，双三次插值还考虑到了不同距离对于像素的影响权重不同，因此双三次插值的放大效果是最好的，同时计算量也是最大的。

参考博客：
​ 双线性插值：https://blog.csdn.net/eurus_/article/details/102755898
​ 双三次插值：https://blog.csdn.net/kill2013110/article/details/108125738

创作不易，使用图片请标注来源，感谢！