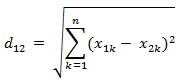浅谈向量检索

浅谈向量检索

背景

索引一直被认为是检索引擎最重要的组成部分，之所以数据库能够快速的查询出来结果。系统设计中很多常见的多种数据结构都是为了快速命中索引设计的， 比如 红黑树、跳跃表、倒排索引、B/B+数， 他们往往都是通过一个关键数据找到整体是否命中。

本文包含多个向量检索的覆盖的知识面，涉及内容比较多，文章比较长

什么是向量

计算机只认识数字，它只能通过数字来量化这个世界，用一组数字来表示一个事物，这样的一组数字就是一个向量（Vector）。如果一个向量由n个数字组成，它就是一个n维向量。拿目前广泛使用的人脸识别技术来说，计算机从照片或视频中提取出人脸的图像，然后将人脸图像转换为128维或者更高维度的向量。

什么是向量检索

首先我们了解下什么是向量，所谓向量就是由n个数字（二值向量由n个比特组成）组成的数组，我们称之为n维向量。而向量检索就是在一个给定向量数据集中，按照某种度量方式，检索出与查询向量相近的K个向量（K-Nearest Neighbor，KNN），但由于KNN计算量过大，我们通常只关注近似近邻（Approximate Nearest Neighbor，ANN）问题。

距离度量

常见的向量度量有四种：欧式距离、余弦、内积、海明距离

• 欧氏距离： 两点之间的线段长度。
  

• 余弦距离：也称为余弦相似度，是用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小的度量，相似度越大越接近于1 [-π/2, π/2]

• 汉明距离：一般作用于二值化向量，二值化的意思是向量的每一列只有 0 或者 1 两种取值。汉明距离的值就两个向量每列数值的异或和，值越小说明越相似，一般用于图片识别，举例：。

  • 1011101与1001001之间的汉明距离是2。
  • 2143896与2233796之间的汉明距离是3。
  • "toned"与"roses"之间的汉明距离是3。

• 曼哈顿距离：计程车几何(Taxicab geometry)或曼哈顿距离(Manhattan distance or Manhattan length)或方格线距离是由十九世纪的赫尔曼·闵可夫斯基所创辞汇，为欧几里得几何度量空间的几何学之用语，用以标明两个点上在标准坐标系上的绝对轴距之总和。

  • 公式：
    

  • 示例：
    

检索方法

向量检索有两类方法 ：存在最近邻检索（Nearest Neighbor Search，NN）和近似最近邻检索（Approximate Nearest Neighbor Search， ANN）

• NN 主要是说对结果进行穷举 ，计算结果也是最为精确。当然也有相关优化例如KD-Tree 但是对于超大量计算还是有些力不从心
• ANN 主要是对结果的一个近似值估计，ANN则是在可接受的精度条件下通过把向量分簇建立索引，大幅提高搜索效率，这也大规模向量检索场景下所使用的主要方法。

ANN的基本思路

ANN检索中典型的做法，分成两步：

• 通过某种聚类算法把大批向量分成很多簇，分簇后的特点如下：

  • 每个簇含有成百上千条向量
  • 每个簇都有一个中心向量
  • 当用户输入目标向量搜索时，系统先把目标向量和每个簇的中心向量做距离计算，挑选出距离比较近的几个簇。

• 把目标向量（Target Vector）和这几个簇里的每一条向量做距离运算，最后得出距离最近的k条结果向量。

举个容易理解栗子

现在我们根据人的年龄、性别、职业、收入、爱好、生活作息、职业等一系列因素。

现在我们通过人物的职业做做一个分类：例如下图中分成了 工程师、律师、医生几个分类

极大的可以减少集合中样本的个数，从而减少计算量。

举个正常的例子

• 假设二维平面中有一堆点，聚类算法把它们分成若干个簇，如图这里分成4簇，黑圈的表示簇的中心向量
• 有一个目标向量，通过计算发现距离黄色部分的中心节点距离最近，则把他归类与黄色部分
• 在黄色部分所有节点都跟这个节点进行距离比较，寻找出距离最近的TopN个节点
  

具体算法

• brute-force搜索的方式是在全空间进行搜索，为了加快查找的速度，几乎所有的ANN方法都是通过对全空间分割，将其分割成很多小的子空间，在搜索的时候，通过某种方式，快速锁定在某一（几）子空间，然后在该（几个）子空间里做遍历。
• ANN的方法分为三大类：基于树的方法、哈希方法、矢量量化方法。

树方法

如 KD-tree，Ball-tree，Annoy

KD-Tree

基于树的经典实现为kd-tree，通过将空间按维度进行划分，缩小检索范围来加速的方法。适用于空间维度较小的情况。Kd-tree 的方法是：找出数据集中方差最高的维度，利用这个维度的数值将数据划分为两个部分，对每个子集重复相同的过程。
简单来讲，就是把数据按照平面分割，并构造二叉树代表这种分割，在检索的时候，可以通过剪枝减少搜索次数。顾名思义，就是暴力比对每一条向量的距离

Annoy

Annoy是一个以树为数据结构的近似最近邻搜索库，并用在Spotify的推荐系统中。Annoy的核心是不断用选取的两个质心的法平面对空间进行分割，最终将每一个区分的子空间里面的样本数据限制在K以内。对于待插入的样本x_i，从根节点依次使用法向量跟x_i做内积运算，从而判断使用法平面的哪一边（左子树or右子树）。对于查询向量q_i，采用同样的方式（在树结构上体现为从根节点向叶子节点递归遍历），即可定位到跟q_i在同一个子空间或者邻近的子空间的样本，这些样本即为q_i近邻。为了提高查询的召回，Annoy采用建立多棵树的方式。

Hash方法

LSH 算法

局部敏感哈希(Local Sensitive Hashing)本质上是一种无监督哈希方法.哈希函数族具备:距离较近的样本点比距离较远的样本点更容易发生碰撞的特点时，就可以被称为局部敏感。
LSH的工作原理：

• 从LSH函数族中随机选择哈希函数，将每个数据点哈希到哈希表中
• 在查询样本的最近邻时，将其做相同的变换，查询样本的最近邻很大概率会在查询样本落入相同的桶中，只需要在桶中进行搜索即可，不用在所有数据集中遍历，进而加速了查找。

关于LSH开源工具库，有很多，这里推荐两个LSH开源工具包：LSHash和FALCONN, 这里就不再赘述，感兴趣的同学可以自行查看。

矢量量化方法

矢量量化方法，即vector quantization，其具体定义为：将一个向量空间中的点用其中的一个有限子集来进行编码的过程。
在矢量量化编码中，关键是码本的建立和码字搜索算法。比如常见的聚类算法，就是一种矢量量化方法。而在ANN近似最近邻搜索中，向量量化方法又以乘积量化(PQ, Product Quantization)最为典型。

乘积量化

乘积量化（Product Quantization，PQ）是一种非常经典实用的矢量量化索引方法，在工业界向量索引中已得到广泛的应用，并作为主要的向量索引方法，在 Faiss 中有非常高效的实现。乘积量化的核心思想是分段（划分子空间）和聚类，或者说具体应用到 ANN 近似最近邻搜索上，KMeans 是 PQ 乘积量化子空间数目为 1 的特例。
矢量量化方法，即 Vector Quantization，其具体定义为：将一个向量空间中的点用其中一个有限子集来进行编码的过程。

码本的建立

• 在训练阶段，针对 N 个训练样本，假设样本维度为 128 维
• 我们将其切分为 4 个子空间，则每一个子空间的维度为 32 维
• 然后我们在每一个子空间中，对子向量采用 KMeans 对其进行聚类（图中示意每个子空间聚成 256类)，这样每一个子空间都能得到一个码本
• 这样训练样本的每个子段，都可以用子空间的聚类中心来近似，对应的编码即为类中心的 ID。

如图所示，通过这样一种编码方式，训练样本仅使用很短的一个编码得以表示， 每个32维的向量最终可以用一个8 bit 的一个聚类中心ID 进行表示，从而达到量化的目的

正如前面所说的，在矢量量化编码中，关键是码本的建立和码字的搜索算法，在上面，我们得到了建立的码本以及量化编码的方式。剩下的重点就是查询样本与 dataset 中的样本距离如何计算的问题了

码字搜索算法

在查询阶段，PQ 同样在计算查询样本与 dataset 中各个样本的距离，只不过这种距离的计算转化为间接近似的方法而获得。PQ 乘积量化方法在计算距离的时候，有两种距离计算方式，一种是对称距离，另外一种是非对称距离。非对称距离的损失小（也就是更接近真实距离），实际中也经常采用这种距离计算方式。下面过程示意的是查询样本来到时，以非对称距离的方式（红框标识出来的部分）计算到 dataset 样本间的计算示意

• 具体地，查询向量来到时，按训练样本生成码本的过程，将其同样分成相同的子段
• 然后在每个子空间中，计算子段到该子空间中所有聚类中心的距离，如图中所示，可以得到 4*256 个距离，这里为便于后面的理解说明，可以把这些算好的距离称作距离表。
• 在计算库中某个样本到查询向量的距离时，比如编码为 (124,56,132,222) 这个样本到查询向量的距离时，我们分别到距离表中取各个子段对应的距离即可，比如编码为 124 这个子段，在第 1 个算出的 256 个距离里面把编号为 124 的那个距离取出来就可，所有子段对应的距离取出来后，将这些子段的距离求和相加，即得到该样本到查询样本间的非对称距离。
• 所有距离算好后，排序后即得到我们最终想要的结果。

简化的核心思路：

• 将原本与N个点的距离运算简化为针对于常数个点的运算的重复运算, 导致对于大量计算来说单个向量的时间复杂度计算从原来的跟向量计算复杂度相关变成一个与向量无关的一次数据查询。
• 如下可以两次计算的差别, 虽然整体时间复杂度没有降低，但是由于距离运算时间在过去时间的大头，导致这样优化的时间是是数量级上的优化：
  • 过去总运算时间 (T_{单次运算时间} + T_遍历时间)* N
  • 现在总运算时间 T_{单次运算时间} * 256 * 4 + T_遍历时间* N

倒排乘积量化

倒排乘积量化(IVFPQ)是 PQ 乘积量化的更进一步加速版。

其加速的本质逃不开在最前面强调的加速原理：brute-force 搜索的方式是在全空间进行搜索，为了加快查找的速度，几乎所有的 ANN 方法都是通过对全空间分割，将其分割成很多小的子空间，在搜索的时候，通过某种方式，快速锁定在某一（几）个子空间，然后在该（几个）子空间里做遍历。
PQ 乘积量化计算距离的时候，距离虽然已经预先算好了，但是对于每个样本到查询样本的距离，还是得老老实实挨个去求和相加计算距离。
但是，实际上我们感兴趣的是那些跟查询样本相近的样本（姑且称这样的区域为感兴趣区域），也就是说老老实实挨个相加其实做了很多的无用功，如果能够通过某种手段快速将全局遍历锁定为感兴趣区域，则可以舍去不必要的全局计算以及排序。

倒排 PQ 乘积量化的”倒排“，正是这样一种思想的体现，在具体实施手段上，采用的是通过聚类的方式实现感兴趣区域的快速定位，在倒排 PQ 乘积量化中，聚类可以说应用得淋漓尽致。

• 在 PQ 乘积量化之前，增加了一个粗量化过程。

  • 具体地，先对 N 个训练样本采用 KMeans 进行聚类，这里聚类的数目一般设置得不应过大，一般设置 1024 差不多，这种可以以比较快的速度完成聚类过程。
  • 得到聚类中心后，针对每一个样本 x_i，找到其距离最近的类中心 c_i 后，两者相减得到样本 x_i 的残差向量(x_i - c_i)，后面剩下的过程，就是针对(x_i - c_i)的 PQ 乘积量化过程，此过程不再赘述。

• 在查询的时候，通过相同的粗量化，可以快速定位到查询向量属于哪个 c_i（即在哪一个感兴趣区域），然后在该感兴趣区域按上面所述的 PQ 乘积量化距离计算方式计算距离。

这里有个小问题，为什么使用残差向量的量化过程， 使用原始向量的量化过程可以不？

整体流程图如下：

量化过程中的思考：

• 向量量化是一种有损压缩。

• 乘积量化中子空间不一定越多越好，要平衡计算复杂度和量化精度，论文推荐选2.

• 类心越多，量化失真(distortion)越小，计算成本也会相应增强。类心数目(centroid)是实际中常调整的超参。

• 乘积量化有个前提假设，两个子空间(subspace)独立。但实际上大多数不是这样，这里引出了OPQ的优化。

  • OPQ(Ge T, He K, Ke Q, et al. Optimized Product Quantization[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2013, 36(4):744-755.)，是针对PQ中子空间存在相关性的优化。主要内容是添加旋转矩阵作用于字典(codebook)，并依次迭代R和聚类，使得最终的量化损失最小。

  • LOPQ(Kalantidis Y , Avrithis Y . Locally Optimized Product Quantization for Approximate Nearest Neighbor Search[C]// 2014 IEEE Conference on Computer Vision and Pattern Recognition. IEEE, 2014.)在OPQ的基础上，加入了每个子空间的各自旋转矩阵。下图展示了不同量化方法下的类心分布。

当然针对于量化方法其实有一个
1.Hervé Jégou, Douze M , Schmid C . Product Quantization for Nearest Neighbor Search[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010.
2.Babenko A, Lempitsky V. The inverted multi-index[C]// Computer Vision & Pattern Recognition. 2012.

临近图方法

HNSW 算法

HNSW 即Hierarchical Navigable Small World, HNSW， 直译过来就分层的可导航小世界。
特点如下：

• 一种基于图的数据结构。
• 使用贪婪搜索算法的变体进行ANN搜索，每次选择最接近查询的未访问的相邻元素时，它都会从元素到另一个元素地遍历整个图，直到达到停止条件。

朴素想法

假设我们现在有13个2维数据向量，我们把这些向量放在了一个平面直角坐标系内，隐去坐标系刻度，它们的位置关系如上图所示。

• 不少人脑子里都冒出过这样的朴素想法，把某些点和点之间连上线，构成一个查找图，存下来备用；
• 当我想查找与粉色点最近的一点时，我从任意一个黑色点出发，计算它和粉色点的距离，与这个任意黑色点有连接关系的点我们称之为“友点”（直译）
• 然后我要计算这个黑色点的所有“友点”与粉色点的距离，从所有“友点”中选出与粉色点最近的一个点，把这个点作为下一个进入点
• 继续按照上面的步骤查找下去。如果当前黑色点对粉色点的距离比所有“友点”都近，终止查找，这个黑色点就是我们要找的离粉色点最近的点。

朴素想法之所以叫朴素想法就是因为它的缺点非常多：

• 首先，我们发现图中的K点是无法被查询到的，因为K点没有友点，怎么办？。
• 其次，如果我们要查找距离粉色点最近的两个点，而这两个近点之间如果没有连线，那么将大大影响效率（比如L和E点，如果L和E有连线，那么我们可以轻易用上述方法查出距离粉色点最近的两个点），怎么办？。
• 最后，D点真的需要这么多“友点”吗？谁是谁的友点应该怎么确定呢？

带着这三个问题，我们进入下一部分：

Delaunay算法

在图论中有一个很好的剖分法则专门解决上一节中提到的朴素想法的缺陷问题------德劳内（Delaunay）三角剖分算法，这个算法可以达成如下要求：

1. 图中每个点都有“友点”。
2. 相近的点都互为“友点”。
3. 图中所有连接（线段）的数量最少。
   

NSW 主要思想

要理解 Hierarchical NSW，要先理解 NSW，即没有分层的可导航小世界的结构。
NSW没有采用德劳内三角剖分法来构成德劳内三角网图，原因之一是德劳内三角剖分构图算法时间复杂度太高，换句话说，构图太耗时。原因之二是德劳内三角形的查找效率并不一定最高，如果初始点和查找点距离很远的话我们需要进行多次跳转才能查到其临近点，需要“高速公路”机制（Expressway mechanism, 这里指部分远点之间拥有线段连接，以便于快速查找）。在理想状态下，我们的算法不仅要满足上面三条需求，还要算法复杂度低，同时配有高速公路机制的构图法。

NSW构图

对于每个新的传入元素，我们从结构中找到其最近邻居的集合（近似的 Delaunay 图）。该集合连接到元素。随着越来越多的元素被插入到结构中，以前用作短距离边现在变成长距离边，形成可导航的小世界。

m=3（每个点在插入时找3个紧邻友点）。

• 第1次构造：图为空，随机插入A，初始点为A。图中只有A，故无法挑选友节点。插入B，B点只有A点可选，所以连接BA。

• 第2次构造：插入F，F只有A和B可以选，所以连接FA，FB。

• 第3次构造：插入C，C点只有A，B，F可选，连接CA，CB，CF。

• 第4次构造：插入E，从A，B，C，F任意一点出发，计算出发点与E的距离和出发点的所有“友节点”和E的距离，选出最近的一点作为新的出发点，如果选出的点就是出发点本身，那么看我们的m等于几，如果不够数，就继续找第二近的点或者第三近的点，本着不找重复点的原则，直到找到3个近点为止。找到了E的三个近点，连接EA，EC，EF。

• 第5次构造：插入D，与E点的插入一模一样，都是在“现成”的图中查找到3个最近的节点作为“友节点”，并做连接。

• 第6次构造：插入G，与E点的插入一模一样，都是在“现成”的图中查找到3个最近的节点作为“友节点”，并做连接。

• 在图构建的早期，很有可能构建出“高速公路”。

• 第n次构造：在这个图的基础上再插入6个点，这6个点有3个和E很近，有3个和A很近，那么距离E最近的3个点中没有A，距离A最近的3个点中也没有E，但因为A和E是构图早期添加的点，A和E有了连线，我们管这种连线叫“高速公路”，在查找时可以提高查找效率（当进入点为E，待查找距离A很近时，我们可以通过AE连线从E直接到达A，而不是一小步一小步分多次跳转到A）。

结论：一个点，越早插入就越容易形成与之相关的“高速公路”连接，越晚插入就越难形成与之相关的“高速公路”连接。

这个算法设计的妙处就在于扔掉德劳内三角构图法，改用“无脑添加”（NSW朴素插入算法），降低了构图算法时间复杂度的同时还带来了数量有限的“高速公路”，加速了查找。

NSW查找

图中的边有两个不同的目的：

• Short-range edges，用作贪婪搜索算法所需的近似 Delaunay 图。
• Long-range edges，用于贪婪搜索的对数缩放。负责构造图形的可导航小世界（NSW）属性。

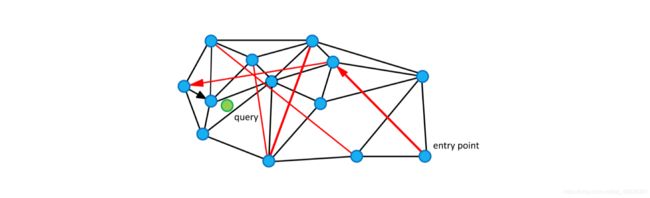
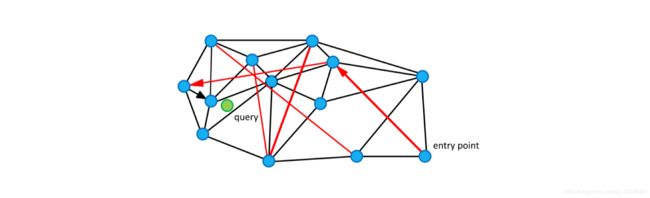
NSW 中的贪婪搜索过程：

• 算法计算从查询 q 到当前顶点的朋友列表的每个顶点的距离，然后选择具有最小距离的顶点。

• 如果查询与所选顶点之间的距离小于查询与当前元素之间的距离，则算法移动到所选顶点，并且它变为新的当前顶点。

• 算法在达到局部最小值时停止：一个顶点，其朋友列表不包含比顶点本身更接近查询的顶点
  ####HNSW
  HNSW 的核心分层结构类似于Redis SortedList底层实现的跳表结构， 不了解的可以自行度娘

  第0层中，是数据集中的所有点，你需要设置一个常数ml，通过公式floor(-ln(uniform(0,1)) x ml)来计算这个点可以深入到第几层。公式中x是乘号，floor() 的含义是向下取整，uniform（0,1）的含义是在均匀分布中随机取出一个值，ln() 表示取对数。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ZMXa48Ww-1629203257851)(http://bos.bj.bce-internal.sdns.baidu.com/agroup-bos-bj/bj-5e86d394161e39f7481483c4e7b51a2f06d2b875)]

• 该算法贪婪地遍历来自上层的元素，直到达到局部最小值。
• 之后，搜索切换到较低层（具有较短 link），从元素重新开始，该元素是前一层中的局部最小值，并且该过程重复。
• 通过采用层状结构，将边按特征半径进行分层，从而将 NSW 的计算复杂度由多重对数（Polylogarithmic）复杂度降到了 对数（logarithmic）复杂度。

参考

文章题目	链接
向量检索	https://bbs.huaweicloud.com/blogs/197840
大规模向量检索	https://zhuanlan.zhihu.com/p/90677337
蚂蚁金服 ZSearch 在向量检索上的探索	https://tech.antfin.com/community/articles/695
大规模特征向量检索算法总结 (LSH PQ HNSW)	https://www.6aiq.com/article/1587522027341
维基百科-汉明距离	https://zh.wikipedia.org/wiki/%E6%B1%89%E6%98%8E%E8%B7%9D%E7%A6%BB
维基百科-曼哈顿距离	https://zh.wikipedia.org/wiki/%E6%9B%BC%E5%93%88%E9%A0%93%E8%B7%9D%E9%9B%A2
一文读懂 ANN	https://flashgene.com/archives/92711.html
ANN搜索算法	https://www.cnblogs.com/ljygoodgoodstudydaydayup/p/10519253.html
向量检索:LSH简介	https://zhuanlan.zhihu.com/p/365658132
Locality Sensitive Hashing(局部敏感哈希)之cross-polytope LSH	https://www.cnblogs.com/gczr/p/12249439.html
matlab sift乘积量化,ANN中乘积量化与多维倒排小结	https://blog.csdn.net/weixin_42306054/article/details/116127725
HNSW	https://www.cnblogs.com/dangui/p/14675121.html
近似最近邻算法 HNSW 学习笔记	https://www.ryanligod.com/2018/11/27/2018-11-27%20HNSW%20%E4%BB%8B%E7%BB%8D/
一文看懂HNSW算法理论的来龙去脉	https://blog.csdn.net/u011233351/article/details/85116719