【图神经网络】10分钟掌握图神经网络及其经典模型

图(Graph)是一种数据结构，能够很自然地建模现实场景中一组实体之间的复杂关系。在真实世界中，很多数据往往以图的形式出现, 例如社交网络、电商购物、蛋白质相互作用关系等。因此，近些年来使用智能化方式来建模分析图结构的研究越来越受到关注, 其中基于深度学习的图建模方法的图神经网络(Graph Neural Network, GNN), 因其出色的性能已广泛应用于社会科学、自然科学等多个领域。

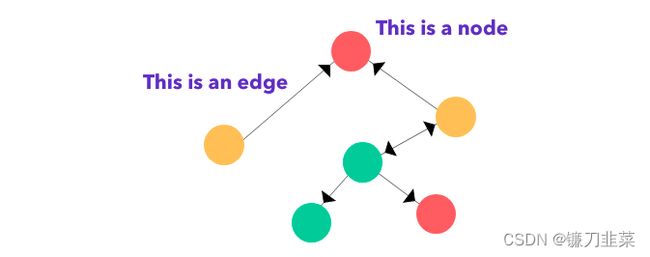
边上面的黑色尖头表示节点之间的关系类型，其可表明一个关系是双向的还是单向的。图有两种主要类型：有向图和无向图。在有向图中，节点之间的连接存在方向；而无向图的连接顺序并不重要。有向图既可以是单向的，也可以是双向的。

图可以表示很多事物——社交网络、分子等等。节点可以表示用户/产品/原子，而边表示它们之间的连接，比如关注/通常与相连接的产品同时购买/键。社交网络图可能看起来像是这样，其中节点是用户，边则是连接：

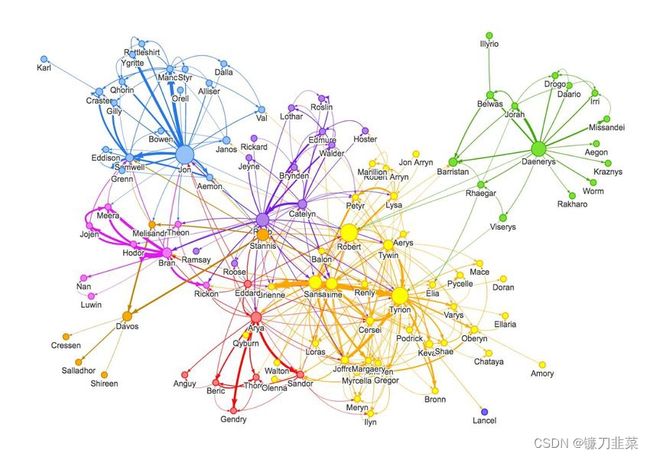
节点表示用户，边则表示两个实体之间的连接/关系。真实的社交网络图往往更加庞大和复杂！

1. 图的基本概念

通常使用$G=(V,E)$来表示图，其中$V$表示节点的集合、$E$表示边的集合。对于两个相邻节点$u,v$, 使用$e=(u,v)$表示这两个节点之间的边。两个节点之间边既可能是有向，也可能无向。若有向，则称之有向图(Directed Graph), 反之，称之为无向图(Undirected Graph)。

1.1 图的表示

在图神经网络中，常见的表示方法有邻接矩阵、度矩阵、拉普拉斯矩阵等。

1. 邻接矩阵(Adjacency Matrix)
   用于表示图中节点之间的关系，对于n个节点的简单图，有邻接矩阵$A\in R^{n\times n}$:$$A_{ij}=\{\begin{array}{ll}1& \text{ if }(v_i,v_j)\in E\text{and}i\ne j\\ 0& \text{ else }\end{array}$$

2. 度矩阵(Degree Matrix)
   节点的度(Degree)表示与该节点相连的边的个数，记作d(v)。对于n个节点的简单图G=(V, E)，其度矩阵D为$D_{ii}=d(v)$，也是一个对角矩阵。

3. 拉普拉斯矩阵 (Laplacian Matrix)
   对于n个节点的简单图$G=(V,E)$，其拉普拉斯矩阵定义为$L=D-A$，其中$D$、$A$为上面提到过的度矩阵和邻接矩阵. 将其归一化后有$L^{sym}=D^{-1/2}L{D}^{-1/2}$。

2. 图神经网络的基本概念

2.1 了解图神经网络

每个节点都有一组定义它的特征。在社交网络图的案例中，这些特征可以是年龄、性别、居住国家、政治倾向等。每条边连接的节点都可能具有相似的特征。这体现了这些节点之间的某种相关性或关系。

假设我们有一个图 G，其具有以下顶点和边：

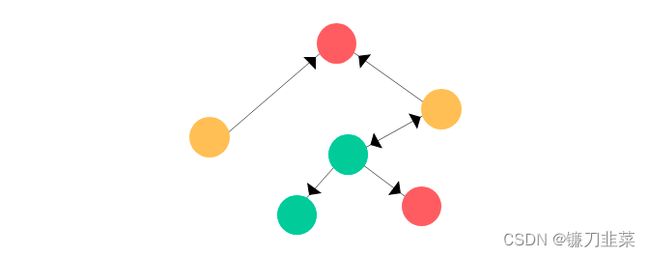
为了简单起见，假设图节点的特征向量是当前节点的索引的one-hot编码。类似地，其标签（或类别）可设为节点的颜色（绿、红、黄）。那么这个图看起来会是这样：

节点的顺序其实并不重要。

注意：在实际运用中，尽量不要使用 one-hot 编码，因为节点的顺序可能会非常混乱。相反，应该使用可明显区分节点的特征，比如对社交网络而言，可选择年龄、性别、政治倾向等特征；对分子研究而言可选择可量化的化学性质。

现在，我们有节点的 one-hot 编码（或嵌入）了，接下来我们将神经网络引入这一混合信息中来实现对图的修改。所有的节点都可转化为循环单元（或其它任何神经网络架构，只是我这里使用的是循环单元）；所有的边都包含简单的前馈神经网络。那么看起来会是这样：

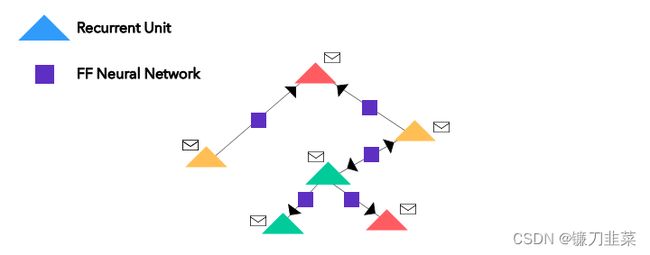
其中的信封符号只是每个节点的 one-hot 编码的向量（嵌入）。

2.2 消息传递

一旦节点和边的转化完成，图就可在节点之间执行消息传递。这个过程也被称为「近邻聚合（Neighbourhood Aggregation）」，因为其涉及到围绕给定节点，通过有向边从周围节点推送消息（即嵌入）。

注意：有时候可为不同类型的边使用不同的神经网络，比如为单向边使用一种神经网络，为双向边使用另一种神经网络。这样仍然可以获取节点之间的空间关系。

就 GNN 而言，对于单个参考节点，近邻节点会通过边神经网络向参考节点上的循环单元传递它们的消息（嵌入）。参考循环单位的新嵌入更新，基于在循环嵌入和近邻节点嵌入的边神经网络输出的和上使用循环函数。我们把上面的红色节点放大看看，并对这一过程进行可视化：

紫色方块是一个应用于来自近邻节点的嵌入（白色信封）上的简单前馈神经网络；红色三角形是应用于当前嵌入（白色信封）和边神经网络输出（黑色信封）之和上的循环函数，以得到新的嵌入（最上面的白色信封）。

这个过程是在网络中的所有节点上并行执行的，因为 L+1 层的嵌入取决于 L 层的嵌入。因此，在实践中，我们并不需要从一个节点「移动」到另一节点就能执行消息传递。

注意：边神经网络输出（黑色信封）之和与输出的顺序无关。

正式地，图神经网络(GNN)最早由Marco Gori、Franco Scarselli等人提出，他们将神经网络方法拓展到了图数据计算领域。在Scarselli论文中典型的图如图1所示：

图1 典型的图神经网络

为了根据输入节点邻居信息更新节点状态，将局部转移函数$f$定义为循环递归函数的形式, 每个节点以周围邻居节点和相连的边作为来源信息来更新自身的表达$h$。为了得到节点的输出$o$, 引入局部输出函数$g$。因此，有以下定义：
$$h_n=f(x_n,x_{co[n]},x_{ne[n]},h_{ne[n]})(1)$$
$$o_n=g(h_n,x_n)(2)$$
其中$x$表示当前节点, $h$表示节点隐状态，$ne[n]$表示表示节点n的邻居节点集合，$co[n]$表示节点n的邻接边的集合。以图1的L1节点为例，$X1$是其输入特征, $ne[l_1]$包含节点$l_2,l_3,l_4,l_6$, $co[l_1]$包含边$l_{(3,1)},l_{(1,4)},l_{(6,1)},l_{(1,2)}$。

将所有局部转移函数$f$堆叠起来, 有：$$H=F(H,X)(3)$$$$O=G(H,X_n)(4)$$其中F是全局转移函数(Global Transition Function), G是全局输出函数(Global Output Function)。
根据巴拿赫不动点定理，假设公式(3)的F是压缩映射，那么不动点H的值就可以唯一确定，根据以下方式迭代求解:
$$H^{t+1}=F(H^t,X)(5)$$基于不动点定理，对于任意初始值，GNN会按照公式(5)收敛到公式(3)描述的解。

2.3 最后的向量表征有什么用？

执行了几次近邻聚合/消息传递流程之后，每个节点的循环单元都会获得一组全新的嵌入。此外，经过多个时间步骤/多轮消息传递之后，节点对自己和近邻节点的信息（特征）也会有更好的了解。这会为整个图创建出更加准确的表征。

要进一步在该流程的更高层面上进行处理或者只是简单地表征该图，你可以将所有嵌入加到一起得到向量 H 来表示整个图。使用 H 比使用邻接矩阵更好，因为不管怎样对图进行扭转变形，这些矩阵都并不表征图的特征或独特性质——只是节点之间的边连接（这在某些情形下并不是很重要）。

总结一下，将所有节点循环单元的最终向量表征加到一起（当然，与顺序无关），然后使用所得到的向量作为其它工作过程的输入或简单地将其用于表征该图。这个步骤看起来如下图所示：

这是经过 n 次重复消息传递之后带有已完全更新的嵌入向量的最终图。可以将所有节点的表征加到一起得到 H。

3. 经典的图神经网络模型

3.1 GCN： Graph Convolution Networks

GCN可谓是图神经网络的“开山之作”，它首次将图像处理中的卷积操作简单的用到图结构数据处理中来，并且给出了具体的推导，这里面涉及到复杂的谱图理论。2017年，Thomas N. Kipf等人提出GCN模型. 其结构如图2所示：

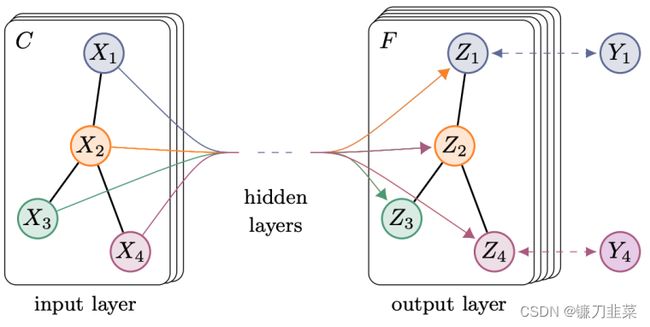
图2 Thomas N. Kipf等人提出GCN

假设需要构造一个两层的GCN，激活函数分别采用ReLU和Softmax，则整体的正向传播的公式如下所示：
$$Z=f(X,A)=softmax(\hat{A}\text{ReLU}(\hat{A}X{W}^{(0)})W^{(1)})(6)$$
$$\hat{A}={\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}(7)$$

其中$W^{(0)}$表示第一层的权重矩阵，$W^{(1)}$表示第二层的权重矩阵，X为节点特征，$\tilde{A}$等于邻接矩阵A和单位矩阵相加，\tilde{D}为$A$的度矩阵。

从上面的正向传播公式和示意图来看，GCN好像跟基础GNN没什么区别。接下里给出GCN的传递公式(8)：
$$H^{(l+1)}=\sigma ({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}{H}^{(l)}{W}^{(l)})(8)$$
观察一下归一化的矩阵与特征向量矩阵的乘积：

这种聚合方式实际上就是在对邻接求和取平均。而${\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}$这种归一化方式，将不再单单地对领域节特征点取平均，它不仅考虑了节点$i$的度，也考虑了邻接节点$j$的度，当邻居节点 $j$ 度数较大时，它在聚合时贡献地会更少。这也比较好理解，存在B->A<-C<-[D,E,F] 这么一个图，当使用这种归一化矩阵，在对A这个节点的特征进行更新时，B占的权重会更大，C占的权重会更小。因为B对A产生影响，与A对B产生对影响是一样的（无向图），由于B只有A这个邻居，所以A对B影响很大；同样地，C对A产生影响，与A对C产生对影响是一样的，因为C有很多节点，所以A对C节点对影响没那么大，即C对A节点对影响没那么大。

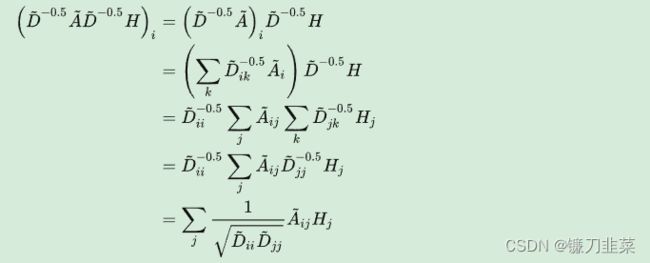
通过实验证明GCN性能出色，GCN即使不训练，提取出来的特征已经非常优秀,作者做了一个实验，使用俱乐部关系网络数据，如图3所示：

图3 GCN在空间上自动聚类从上图可以发现，使用随机初始化的GCN进行特征提取，经过GCN的提取出的embedding，已经在空间上自动聚类了。

GCN的缺点：第一，GCN需要将整个图放到内存和显存，这将非常耗内存和显存，处理不了大图；第二，GCN在训练时需要知道整个图的结构信息(包括待预测的节点), 这在现实某些任务中也不能实现(比如用今天训练的图模型预测明天的数据，那么明天的节点是拿不到的)。

3.2 GraphSAGE：归纳式学习框架

为了解决GCN的两个缺点问题，GraphSAGE被提了出来。在介绍GraphSAGE之前，先介绍一下Inductive learning和Transductive learning。注意到图数据和其他类型数据的不同，图数据中的每一个节点可以通过边的关系利用其他节点的信息。这就导致一个问题，GCN输入了整个图，训练节点收集邻居节点信息的时候，用到了测试和验证集的样本，我们把这个称为Transductive learning。

然而，我们所处理的大多数的机器学习问题都是Inductive learning，因为我们刻意的将样本集分为训练/验证/测试，并且训练的时候只用训练样本。这样对图来说有个好处，可以处理图中新来的节点，可以利用已知节点的信息为未知节点生成embedding，GraphSAGE就是这么干的。

提到GraphSAGE模型, 不得不又提到GCN，回顾上面的GCN的迭代公式：

图中红框位置所做的操作可以简单理解为对邻接矩阵A的归一化变换，去掉该部分会发现剩下的结构等同于深度神经网络，加上红色部分后，通过矩阵乘法实际上所做的就是将节点与节点相邻节点特征信息进行相加。

GraphSAGE在特征聚合方式上与GCN简单相加不同，GraphSAGE支持max-pooling、LSTM、mean等聚合方式。另外，GraphSAGE与GCN的最大不同点在于，GCN是直推式方法，即所有节点都在图中，对于新出现的节点无法处理。GraphSAGE是归纳式，对于没见过的节点也能生成embedding。

GraphSAGE的传播方法如图6所示：

可以看到对于图G中的某个节点v，需要聚合k层信息，那么先有个对层数遍历的for循环，第二层循环便是遍历节点v的邻居节点，然后通过聚合函数AGGEGATE(可以是mean、max、LSTM或者其他)来聚合k-1层的邻居节点信息，得到聚合后的k层邻居节点信息，然后将聚合后的k层邻居节点信息与k-1层节点v的信息进行拼接，然后通过权重参数W进行计算得到K层关于节点v的信息。

GraphSAGE是一个Inductive Learning框架，具体实现中，训练时它仅仅保留训练样本到训练样本的边，然后包含Sample和Aggregate两大步骤，Sample是指如何对邻居的个数进行采样，Aggregate是指拿到邻居节点的embedding之后如何汇聚这些embedding以更新自己的embedding信息。下图展示了GraphSAGE学习的一个过程：

以为红色节点为目标节点，在一次步骤中，对红色节点的一阶邻居和二阶段邻居做随机采样。然后通过聚合策略，把节点的特征信息从二阶邻居聚合到目标节点上，然后用更新后的目标节点的表征可以应用到不同需求的任务上。

为了看的更清晰，我们将更新某个节点的过程展开来看，如下图分别为更新节点A和更新节点B的过程，可以看到更新不同的节点过程每一层网络中聚合器和权重矩阵都是共享的。

那么GraphSAGE Sample是怎么做的呢？GraphSAGE是采用定长抽样的方法，具体来说，定义需要的邻居个数S ，然后采用有放回的重采样/负采样方法达到 S。保证每个节点（采样后的）邻居个数一致，这样是为了把多个节点以及它们的邻居拼接成Tensor送到GPU中进行批训练。

那么GraphSAGE 有哪些聚合器呢？主要有三个：

这里说明的一点是Mean Aggregator和GCN的做法基本是一致的（GCN实际上是求和）。

到此为止，整个模型的架构就讲完了，那么GraphSAGE是如何学习聚合器的参数以及权重矩阵W呢？

• 如果是有监督的情况下，可以使用每个节点的预测lable和真实lable的交叉熵作为损失函数。
• 如果是在无监督的情况下，可以假设相邻的节点的embedding表示尽可能相近，因此可以设计出如下的损失函数：
  
  GraphSAGE相对于GCN可以避免需要一次性加载整张网络、能够灵活设计聚合方式、具备Transductive性质。可以适配测试集的节点变化，不需要像GCN一样会因为节点变化造成拉普拉斯矩阵变化导致需要重新训练模型。

总结一下，GraphSAGE的一些优点：
（1）利用采样机制，很好的解决了GCN必须要知道全部图的信息问题，克服了GCN训练时内存和显存的限制，即使对于未知的新节点，也能得到其表示；
（2）聚合器和权重矩阵的参数对于所有的节点是共享的；
（3）模型的参数的数量与图的节点个数无关，这使得GraphSAGE能够处理更大的图；
（4）既能处理有监督任务也能处理无监督任务。

GraphSAGE也有一些缺点，每个节点那么多邻居，GraphSAGE的采样没有考虑到不同邻居节点的重要性不同，而且聚合计算的时候邻居节点的重要性和当前节点也是不同的。

3.3 GAT：Attention机制

为了解决GNN聚合邻居节点的时候没有考虑到不同的邻居节点重要性不同的问题，GAT借鉴了Transformer的idea，引入masked self-attention机制，在计算图中的每个节点的表示的时候，会根据邻居节点特征的不同来为其分配不同的权值。

具体地，首先来介绍单个的graph attentional layer。单个的 graph attentional layer 的输入是一个节点特征向量集：$h=\{h_1,h_2,...,h_N\},h_i\in {\mathbb{R}}^F$其中，N表示节点集中节点的个数，F表示相应的特征向量维度。每一层的输出是一个新的节点特征向量集：$h^{\prime }=\{{h^{\prime }}_1,{h^{\prime }}_2,...,{h^{\prime }}_N\},{h^{\prime }}_i\in {\mathbb{R}}^{F^{\prime }}$,其中，$F^{\prime }$表示新的节点特征向量维度（可以不等于$F$）。

一个graph attention layer的结构如图4所示,节点$i，j$的特征作为输出，计算两节点之间的注意力权重。

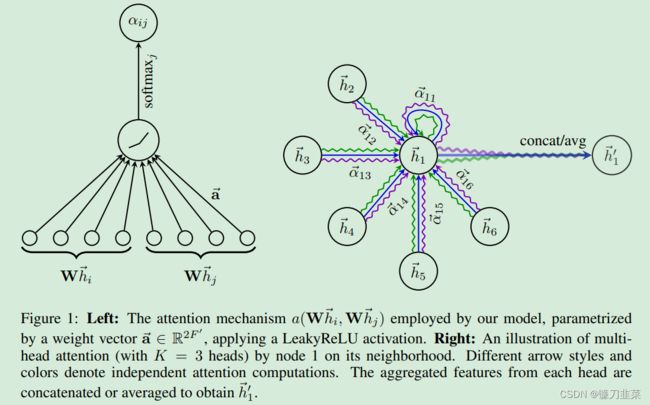
为了将输入特征转换为高维特征（增维）以获得足够的表达能力，每个节点将经过一个共享的线性变换，该模块的参数用权重矩阵$W\in {\mathbb{R}}^{F^{\prime }\times F}$来表示，对某个节点做线性变换可表示为 $W{h}_i\in {\mathbb{R}}^{F^{\prime }}$。这是一种常见的特征增强（feature augment）方法。

同样是在每个节点间共享self-attention机制：$a:{\mathbb{R}}^{F^{\prime }}\times {\mathbb{R}}^{F^{\prime }}\to \mathbb{R}$，可计算节点$i$和$j$之间的attention 系数如下：$$e_{ij}=a(W{h}_i,W{h}_j)$$该系数表示了节点$i$的特征对节点$j$的重要性。注意机制$a(\cdot )$是一个单层前馈神经网络，用一个权重向量来表示：$a\in {\mathbb{R}}^{2F^{\prime }}$，它把拼接后的长度为$2F$的高维特征映射到一个实数上，作为注意力系数。

attention 机制分为以下两种：

1. Global graph attention：允许每个节点参与其他任意节点的注意力机制，它忽略了所有的图结构信息。
2. Masked graph attention：只允许邻接节点参与当前节点的注意力机制中，进而引入了图的结构信息。

论文种采用Masked graph attention，并且邻接节点是一阶邻接节点（包括节点本身）。

为了使不同节点间的注意力系数易于比较，使用softmax函数对所有对于节点$i$的注意力系数进行归一化。上述注意力机制，采用共享权重线性变换、Masked self attention 和 LeakyReLU非线性（negative input slope α = 0.2）归一化后的计算公式如下，其中 T表示转置，||表示拼接：

在得到归一化的注意力系数之后，可以通过对邻接节点特征的线性组合经过一个非线性激活函数来更新节点自身的特征作为输出：$${h^{\prime }}_i=\sigma (\sum _{j\in {\mathcal{N}}_i}{\alpha }_{ij}W{h}_j)$$

为了稳定self-attention的学习过程，GAT原文使用多头注意力机制（Multi-head attention）。具体地，使$K$个独立注意力机制根据上式进行变换，得到更新的节点输出特征，然后将$K$个特征拼接（concat），得到如下输出特征：

如果我们在最后一层（预测层）使用Multi-head attention mechanism，需要把输出进行平均化，再使用非线性函数（softmax或logistic sigmoid），公式如下：

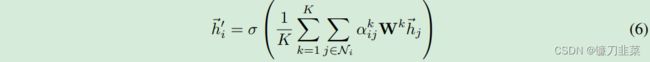
多头注意力本质是引入并行的几个独立的注意力机制，可以提取信息中的多重含义，防止过拟合。

总结一下，GAT的一些优点：
（1）训练GCN无需了解整个图结构，只需知道每个节点的邻居节点即可；
（2）计算速度快，可以在不同的节点上进行并行计算；
（3）既可以用于Transductive Learning，又可以用于Inductive Learning，可以对未见过的图结构进行处理。

4. 流行的图神经网络模型

4.1 无监督的节点表示学习（Unsupervised Node Representation）

由于标注数据的成本非常高，如果能够利用无监督的方法很好的学习到节点的表示，将会有巨大的价值和意义，例如找到相同兴趣的社区、发现大规模的图中有趣的结构等等。

这其中比较经典的模型有GraphSAGE、Graph Auto-Encoder（GAE）等，GraphSAGE就是一种很好的无监督表示学习的方法，前面已经介绍了，这里就不赘述。

4.1.1 GAE: Graph Auto-Encoder

在介绍Graph Auto-Encoder之前，需要先了解自编码器(Auto-Encoder)、变分自编码器(Variational Auto-Encoder)，这里就不赘述。理解了自编码器之后，再来理解变分图的自编码器就容易多了。如下图所示，输入图的邻接矩阵A 和节点的特征矩阵X，通过编码器（图卷积网络）学习节点低维向量表示的均值$\mu$和方差$\sigma$，然后用解码器（链路预测）生成图。

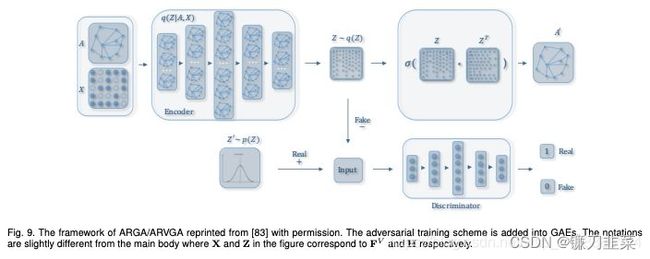
编码器（Encoder）采用简单的三层GCN网络，解码器（Encoder）计算两点之间存在边的概率来重构图，损失函数包括生成图和原始图之间的距离度量，以及节点表示向量分布和正态分布的KL-散度两部分。具体公式如图12所示：

另外为了做比较，论文作者还提出了图自编码器(Graph Auto-Encoder)，相比于变分图的自编码器，图自编码器就简单多了，Encoder是两层GCN，Loss只包含Reconstruction Loss。

4.2 Graph Pooling

Graph pooling是GNN中很流行的一种操作，目的是为了获取一整个图的表示，主要用于处理图级别的分类任务，例如在有监督的图分类、文档分类等等。

Graph pooling的方法有很多，如简单的max pooling和mean pooling，然而这两种pooling不高效而且忽视了节点的顺序信息；这里介绍一种方法：Differentiable Pooling (DiffPool)。

4.2.1 DiffPool

在图级别的任务当中，当前的很多方法是将所有的节点嵌入进行全局池化，忽略了图中可能存在的任何层级结构，这对于图的分类任务来说尤其成问题，因为其目标是预测整个图的标签。针对这个问题，斯坦福大学团队提出了一个用于图分类的可微池化操作模块——DiffPool，可以生成图的层级表示，并且可以以端到端的方式被各种图神经网络整合。

DiffPool的核心思想是通过一个可微池化操作模块去分层地聚合图节点，具体的，这个可微池化操作模块基于GNN上一层生成的节点嵌入X以及分配矩阵S ，以端到端的方式分配给下一层的簇，然后将这些簇输入到GNN下一层，进而实现用分层的方式堆叠多个GNN层的想法。

具体地，给定一个GNN模块的输出$Z=\text{GNN}(A，X)$和一个图的邻接矩阵$A\in {\mathbb{R}}^{n\times n}$，目标是寻找一种方式可以得到一个新的包含$m<n$个节点的粗化图（coarsened graph），其中这个新图的邻接矩阵为$A^{\prime }\in {\mathbb{R}}^{m\times m}$, 节点embedding矩阵为$Z^{\prime }\in {\mathbb{R}}^{m\times d}$。

这个新的粗化图（coarsened graph）作为下一层GNN的输入，重复L次就可到了一些列的coarser。因此，目标就是需要学习一种pooling策略，这种策略可以泛化到具有不同节点、边的图中，并且能够在推理过程中能适应不同的图结构。

那么这个节点嵌入和分配矩阵是怎么算的？计算完之后又是怎么分配给下一层的？这里就涉及到两部分内容，一个是分配矩阵的学习，一个是池化分配矩阵。
（1）池化分配矩阵(Pooling with an assignment matrix)
定义第$l$层学到的cluster assignment matrix为$S^{(l)}\in {\mathbb{R}}^{n_l\times n_{l+1}}$，$n_l$表示在第$l$层的节点数，$n_{l+1}$表示在第$l+1$层的节点数，$n_l>n_{l+1}$，即行数等于第$l$层的节点数（cluster数），列数代表第$l+1$层的节点数（cluster数）。assignment matrix表示第$l$层的每一个节点到第$l+1$层的每一个节点（或cluster）的概率。

假设$S^{(l)}$是预先计算好的。DIFFPOOL层$\left(A^{(l+1)},X^{(l+1)}\right)=\mathrm{DIFFPOOL}\left(A^{(l)},Z^{(l)}\right)$表示粗化输入图，然后生成一个新的邻接矩阵$A^{(l+1)}$和新的embeddings矩阵$X^{(l+1)}$:
$$X^{(l+1)}=S^{(l{)}^T}{Z}^{(l)}\in {\mathbb{R}}^{n_{l+1}\times d}$$
$X_i^{(l+1)}$表示第$l+1$层cluster $i$的embedding
$$A^{(l+1)}=S^{(l{)}^T}{A}^{(l)}{S}^{(l)}\in {\mathbb{R}}^{n_{l+1}\times n_{l+1}}$$
$A_{ij}^{(l+1)}$表示第$l+1$层cluster i和cluster j之间的连接强度

（2）分配矩阵的学习（Learning the assignment matrix）
下面介绍DIFFPOOL如何用公式上述两个公式生成assignment矩阵$S^{(l)}$和embedding矩阵$Z^{(l)}$：
$$Z^{(l)}={\mathrm{GNN}}_{l,\text{ embed }}\left(A^{(l)},X^{(l)}\right)\text{\hspace{1em}(5)}$$
$$S^{(l)}=\mathrm{softmax}\left({\mathrm{GNN}}_{l,\mathrm{pool}}\left(A^{(l)},X^{(l)}\right)\right)\text{\hspace{1em}(6)}$$
其中：

• ${\mathrm{GNN}}_{l,\mathrm{pool}}$表示第$l$层的pooling GNN
• ${\mathrm{GNN}}_{l,\mathrm{pool}}$的输出维数对应于第 l 层预定义的最大cluster数，是模型的超参数使用cluster的邻接矩阵$A^{(l)}$和特征矩阵$X^{(l)}$生成一个assignment矩阵

这两个GNN使用相同的输入数据，但具有不同的参数，并扮演不同的角色：embedding GNN为这一层的输入节点生成新的embedding，而pooling GNN生成从输入节点到$n_{l+1}$个cluster的概率。

在倒数第二层，即L-1层时令assignment矩阵是一个全为1的向量，也就是说所有在最后的L层的节点都会被分到一个cluster，生成对应于整图的一个embedding向量。这个embedding向量可以作为可微分类器（如softmax层）的特征输入，整个系统可以使用随机梯度下降进行端到端的训练。

总结一下DiffPool的优点：
（1）可以学习层次化的pooling策略；
（2）可以学习到图的层次化表示；
（3）可以以端到端的方式被各种图神经网络整合。

DiffPool也有其局限性，分配矩阵需要很大的空间去存储，空间复杂度为$O(k{V}^2)$， $k$为池化层的层数，所以无法处理很大的图。

5. 实现图神经网络的步骤

GNN 用起来相当简单。事实上，实现它们涉及到以下四个步骤：

1. 给定一个图，首先将节点转换为循环单元，将边转换为前馈神经网络；
2. 接着为所有节点执行 n 次近邻聚合（也就是消息传递）；
3. 然后再在所有节点的嵌入向量上求和以得到图表征 H；
4. 最后可以完全跳过 H 直接向更高层级进发或者也可使用 H 来表征该图的独有性质。

6. 推荐书籍

《Graphs, Networks and Algorithms》 第四版：在过去的几十年里，组合优化和图论——作为组合学的整个领域——经历了特别快速的发展。这一事实有多种原因；一个是，例如，应用组合论证已经变得越来越普遍。然而，数学之外的两个发展可能更为重要：首先，组合优化的许多问题直接产生于工程和管理的日常实践；确定交通或通信网络中最短或最可靠的路径，最大或相容的流量，或最短的线路；规划交通网络的连接；协调项目；解决供需问题。第二，随着越来越高效的计算机系统的发展，那些属于运筹学的任务的实际实例已经可以得到。此外，组合优化问题对复杂性理论也很重要，复杂性理论是数学和理论计算机科学的交叉领域，涉及算法分析。组合优化是数学中令人着迷的一部分，它的魅力——至少对我来说——很大程度上来自于它的跨学科性和实用性。本书主要介绍了可以用图论方法表述和处理的组合优化部分；既不考虑线性规划理论，也不考虑多面体组合理论。
https://www.springer.com/gp/book/9783642322778

参考资料

1. 《图深度学习》 马耀 汤继良 著
2. 《深入浅出图神经网络：GNN原理解析》 刘忠雨 李彦霖 周洋 著
3. Stanford CS224W Tutorials
4. 一文读懂图神经网络
5. 人工智能中图神经网络GNN是什么？
6. 图神经网络从入门到入门
7. 巴拿赫不动点定理
8. https://zhuanlan.zhihu.com/p/112277874
9. Kipf T N , Welling M . Semi-Supervised Classification with Graph Convolutional Networks[J]. 2016.
10. Velikovi P , Cucurull G , Casanova A , et al. Graph Attention Networks[J]. 2017.
11. W. Hamilton, Z. Ying and J. Leskovec, “Inductive representation learning on large graphs” in Advances in Neural Information Processing Systems, pp. 1025-1035, 2017.
12. VGAE（Variational graph auto-encoders）论文详解
13. Hierarchical Graph Representation Learning with Differentiable Pooling 图分类 NeurIPS 2018