蓝桥杯倒计时 | 倒计时17天

作者️‍♂️：让机器理解语言か

专栏：蓝桥杯倒计时冲刺

描述：蓝桥杯冲刺阶段，一定要沉住气，一步一个脚印，胜利就在前方！

寄语：没有白走的路，每一步都算数！

 题目一：22年省赛A题——小兰做实验 (难度：★★)

小蓝做实验 - 蓝桥云课 (lanqiao.cn)

问题描述

小蓝很喜欢科研, 他最近做了一个实验得到了一批实验数据, 一共是两百 万个正整数。

如果按照预期, 所有的实验数据 x 都应该满足 。但是做实验都会有一些误差, 会导致出现一些预期外的数据, 这种误差数据 y 的 范围是 1 。由于小蓝做实验很可靠, 所以他所有的实验数据中 99.99% 以上都是符合预期的。小蓝的所有实验数据都在 primes.txt 中, 现 在他想统计这两百万个正整

数中有多少个是质数, 你能告诉他吗?

答案提交

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一 个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。

【思路】 

三个考点:

1. 读文件。文件有200万个整数，只能读文件，不能复制到代码中。
2. 素数判断。判断x是否为素数，可以把它除以[2, sqrt(x)]内的素数，如果能整除，就不是素数。
3. 素数筛，预处理出素数。文件里99.99%的整数都< 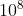，所以只要得到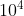内的素数即可。约1300个素数。其他0.01%的大于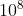的数，数量很少，可以单独判断。

 计算量:1300×200万。
Python代码实际运行时间:约1分钟。

【代码】

注意：在IDLE运行时，代码和文件必须在同一个文件夹内。

from math import *

def E_sieve(n):     # 得到10^4以内的素数
  for i in range (2,int (sqrt (n)+1)):
    if not vis[i]:
      for j in range(i*i, n+1,i):
        vis[j] =1
  k = 0 
  for i in range(2,n+1):#存素数
    if not vis[i]:
      prime[k] = i
      k += 1
    return k

def is_prime(x):  # 判断素数：若n是素数，返回true
  if x == 1: return False #1不是素数
  for i in range(k):
    if x % prime[i] == 0: return False #不是素数
  return True     #是素数

cnt = 0
N = int(1e4)
prime =[0]*N
vis =[0]*N
n = int(1e4)
k = E_sieve(n-1)
print(k)    #质数个数
with open ('primes.txt','r') as f:    # 读取文件
  for a in f:
    b=int(a.rstrip())                 #去掉末尾的\n，转为整数
    if b<=int(1e8):
      if is_prime(b)==True:cnt +=1
      #else:#单独判断大于1e8的数字
print(cnt)

题目二：22年省赛B题——火柴棒数字 (难度：★★★) 

火柴棒数字 - 蓝桥云课 (lanqiao.cn)

问题描述

小蓝最近迷上了用火柴棒拼数字字符, 方法如下图所示:

他只能拼 0 至 9 这十种数字字符, 其中每个数字字符需要的火柴棒的数目 依次是: 6,2,5,5,4,5,6,3,7,6 。他不喜欢重复拼同一个数字字符, 所以对于每个 数字字符他最多拼十个。小蓝会把拼出来的数字字符组合在一起形成一个整数, 例如对于整数 345 , 需要的火柴棒的数目为 5+4+5=14 根。小蓝有 300 根 火柴棒, 他想知道自己能拼出的最大整数是多少? 可以不使用完这 300 根火柴 棒, 可以有多余的火柴棒剩下。

答案提交

这是一道结果填空的题, 你只需要算出结果后提交即可。本题的结果为一 个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。

【思路】 

将数字看成价值为1且各有10个的物品，需要的火柴棒看成重量，这是多重背包问题。因为是填空题，没有用滚动数组优化和二进制优化。

• 为什么每个数字价值都为1？

答：因为位数越大，这个整数就越大，最大的整数肯定是位数最多的。（例如：9999＜10000），每个数字都相当于给你增加了一位数， 所以每个数字价值都为1。

•  位数相同（价值相同）时，怎么选择？

数字是从小到大装进dp[ ][ ]，为了拼出最大的整数，所以输出最大整数时应该按数字i从大到小考虑。当位数相同的时候就选择装了更多数字i的dp，因为装了更多数字i的dp肯定比装了较少的数字i的dp，最后拼出的整数更大。

• 定义状态dpli][j]：表示把前i个数字装进容量j的背包，能装进背包的最大价值。

【代码】 

N = 300                           # 背包容量
W =[0,6,2,5,5,4,5,6,3,7,6]        # 每种火柴的重量
dp = [[0]*301 for i in range(11)]
for i in range(1,11):             # 遍历所有数字：数字0为1，数字1为2，以此类推。
  for k in range(0,11):           # 每个数字最多有10个，每个价值为1
    for j in range(k * W[i],301): # 枚举背包容量
      dp[i][j] = max(dp[i-1][j], dp[i - 1][j - k * W[i]] + k) # 不装或装第i个数的两种情况取最大值
j=300
for i in range(10,0,-1):    # 遍历所有数字，数字9为10，数字8为9，以此类推
  k= 0 
  # 在最大价值下（dp[i][j]）最多能装k个数字i
  for g in range(0,11):     # 遍历每种数字的数量
    if j-g*W[i]>=0:         # 背包放得下
      if (dp[i][j] == dp[i - 1][j - g * W[i]] + g): # 位数（最大价值）相同时，能否装下g个数字i
        k = g         # 记录最多能装k个
  j = j - k * W[i]    # 背包剩余容量
  while k > 0:        # 装了这个数字k个，就输出k个这个数字
    k -= 1
    print(i - 1, end='') 
# 答案：9999999999777777777755555555554444444444333333333322222222221111

题目三：22年省赛C题——近似GCD (难度：★★★)

问题描述

小蓝有一个长度为 n 的数组 A=(a1​,a2​,⋯,an​), 数组的子数组被定义为从原数组中选出连续的一个或多个元素组成的数组。数组的最大公约数指的是数组中所有元素的最大公约数。如果最多更改数组中的一个元素之后, 数组的最大公约数为 g, 那么称 g 为这个数组的近似 GCD。一个数组的近似 GCD 可能 有多种取值。

具体的, 判断 g 是否为一个子数组的近似 GCD 如下:

1. 如果这个子数组的最大公约数就是 g, 那么说明 g 是其近似 GCD。

2. 在修改这个子数组中的一个元素之后 (可以改成想要的任何值), 子数组的最大公约数为 g, 那么说明 g 是这个子数组的近似 GCD。

小蓝想知道, 数组 A 有多少个长度大于等于 2 的子数组满足近似 GCD 的 值为 g 。

输入格式

输入的第一行包含两个整数 n,g, 用一个空格分隔, 分别表示数组 A 的长 度和 g 的值。

第二行包含 n 个整数 a1​,a2​,⋯,an​, 相邻两个整数之间用一个空格分隔。

输出格式

输出一行包含一个整数表示数组 A 有多少个长度大于等于 2 的子数组的近 似 GCD 的值为 g 。

样例输入

5 3
1 3 6 4 10

样例输出

5

样例说明

满足条件的子数组有 5 个:

[1,3]: 将 1 修改为 3 后, 这个子数组的最大公约数为 3 , 满足条件。

[1,3,6]: 将 1 修改为 3 后, 这个子数组的最大公约数为 3 , 满足条件。

[3,6]：这个子数组的最大公约数就是 3 , 满足条件。

[3,6,4] : 将 4 修改为 3 后, 这个子数组的最大公约数为 3 , 满足条件。

[6,4] : 将 4 修改为 3 后, 这个子数组的最大公约数为 3 , 满足条件。

评测用例规模与约定

对于 20% 的评测用例, 2≤n≤10^2 ；

对于 40% 的评测用例, 2≤n≤10^3;

对于所有评测用例, 2≤n≤1≤g,ai​≤10^9 。

n最大是 ，所以最多只能用O(nlogn)的算法。

【思路】 

题解
一个子数组a:

• 若a中每一项都是g的倍数，只需要将a中某个元素改为g，满足要求。
• 若a中存在一个不是g的倍数，把它改为g，满足要求。
• 若a中存在至少2个不是g的倍数，无法满足要求。

问题变成：求原数组有多少个子数组满足这个数组里最多只有一个元素不是g的倍数编码

用双指针遍历原数组：双指针复杂度：O(n)

【代码】 

        技巧1：用last标记当前的不满足g的倍数的点，下次a[i]再次不满足g的倍数时，j直接跳到last往后一点（即last+1），确保只有一个不是g的倍数

        技巧2： 每次i移动一步就记录一下双指针的距离（即满足要求的子数组个数），然后将它们累加起来，就是所有满足要求的子数组个数

n,g=map(int,input().split())
a=[0]+list(map(int,input().split()))
ans=0
last=0
j=1
for i in range(1, n+1):    # 前指针往前走
  if a[i]%g != 0:          # 不满足g的倍数
    j = last+1             # 后指针往前走
    last = i               # last标记不满足点，下次a[i]再次不满足g的倍数，j直接跳到last往后一点
  if i-j+1 >= 2:ans += i-j    # 长度大于2就开始累加
print(ans)