tensorflow学习笔记一

1、tensorflow中的数据类型

import tensorflow as tf
import numpy as np

# 张量可以是数字、列表、ndarray

# 使用列表创建张量
print(tf.constant([2,3]))
print(tf.constant([[2,3],[1,4]]))

# tensorflow2 默认使用Eager动态图机制
print(type(tf.constant([[2,3],[1,4]])))

# 使用numpy数组创建张量时，如果不指定数据类型会使用numpy中元素的数据类型
print(tf.constant(np.array([1,2])))
# float64
print(tf.constant(np.array([1.0,2.0])))
# tensorflow中float32运算的速度远远高于float64，一般float32的精度足够使用，
# 所以使用numpy创建张量时，建议指定类型为tf.float32
print(tf.constant(np.array([1.0,2.0]), dtype=tf.float32))

# cast转换tensor的数据类型
a = tf.constant(np.array([1,2]))
b = tf.cast(a, dtype=tf.float32)
print(b)

# 进行数据类型转换时，一般是低精度数据类型向高精度数据类型转换，否则会发生数据溢出，得出错误结果
a = tf.constant(123456789, dtype=tf.int32)
b = tf.cast(a, dtype=tf.int16)
print(b)

# 可以指定通过cpu或gpu创建tensor
with tf.device("cpu"):
    a = tf.constant(1)
with tf.device("gpu"):
    b = tf.constant([2,3])
print(a.device)
print(b.device)

# 将tensor在cpu和gpu之间转移，一个tensor在cpu上，一个tensor在gpu上，这两个tensor是不能直接运算的，必须都在cpu或都在gpu才能运算
aa = a.gpu()
bb = b.cpu()
print(aa.device)
print(bb.device)

# tensor通过ndim获取维度，tf.rank同样可以获取tensor的维度，但是返回结果也是一个tensor
print(b.ndim)
print(tf.rank(b))

c = np.array([33,44])
print(c)

# 使用tf.is_tensor或isinstance方法判断数据是不是一个tensor，isinstance不推荐使用
print(isinstance(c, tf.Tensor))
print(tf.is_tensor(c))

print('=========================')
a = np.arange(5)
print(tf.convert_to_tensor(a))

# tf.Variable创建一个可优化的变量，求导的时候会对这个变量求偏导
b = tf.Variable(a)
print(b)
print(b.trainable)

# tensor通过numpy()方法取出tensor中的数据，int，float同理
b = tf.constant(4)
print(b.numpy())
print(int(b))
print(float(b))

2、创建tensor

import tensorflow as tf
import numpy as np

# 创建2行1列全为1的张量
print(tf.ones(shape=(2, 1)))
# 创建6行2列全为1的张量
print(tf.ones([6, 2]))
print(tf.ones([8], dtype=tf.int64))
print(tf.zeros(shape=(2, 3)))
# tf.zeros使用方法与tf.ones完全相同

# tf.fill创建元素值都相同的张量，可以替代tf.zeros与tf.ones，tf.fill没有dtype，根据传入数据自动判断元素类型
print(tf.fill(dims=(3, 3), value=9))

# tf.constant也可以创建元素值都相同的张量
print(tf.constant(value=9, shape=(4, 4)))

# 创建3*3*3的张量，服从正态分布，均值为1，标准差为2
print(tf.random.normal(shape=(3, 3, 3), mean=1, stddev=2))

# truncated_normal创建一个截断的正态分布，截断标准为2倍的标准差，
# 也就是说不会创建偏离均值超过2倍标准差的值，从而防止个别元素与其他元素差异过大，
# 例如当均值为2，标准差为3，不会出现[-4,8]之外的值
print(tf.random.truncated_normal(shape=(4, 4), mean=2, stddev=3))

# tf.random.set_seed设置随机种子
tf.random.set_seed(8)
print(tf.random.normal(shape=(3,3)))
tf.random.set_seed(8)
print(tf.random.normal(shape=(3,3)))

# tf.random.uniform创建均匀分布张量
print(tf.random.uniform(shape=(3,3),minval=100, maxval=110))

# tf.random.shuffle将张量沿着第一维打乱
x = tf.constant([[1,2],[3,4],[5,6]])
print(tf.random.shuffle(x))
# 对于更高维度的张量，shuffle也只沿着第一维打乱

# 创建序列，delta步长
print(tf.range(2,10, delta=1))

# zeros_like等同于tf.zeros(x.shape)
print(tf.zeros_like(x))
print(tf.ones_like(x))

当张量在cpu上运行时，张量和NumPy其实是共享同一段内存，只是读出和理解它的方式不同，因此这种情况下使用张量的numpy方法，可以非常快的得到结果

当张量在gpu上运行时，就把内存中的numpy的内容拷贝一份到gpu的显存中，在gpu中做高速运算，这时如果用numpy方法读取它的值，就需要再从gpu的显存中拷贝到内存中，然后再以numpy数组的形式输出，因此速度会比较慢。

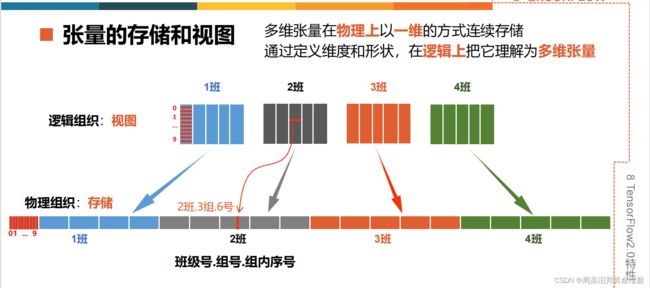
3、维度变换

当对多维张量进行维度变换时，只是改变了逻辑上索引的方式，没有改变内存中的存储方式

import numpy as np
import tensorflow as tf

# tf.reshape改变张量的维度
a = tf.range(24)
print(tf.reshape(tensor=a, shape=(2, 3, 4)))

print('=======================')
# 也可以先创建一个n维数组然后用tf.constant转换成张量
b = np.arange(24).reshape(2, 3, 4)
print(tf.constant(b))

# shape参数=-1：自动推导出长度
print(tf.reshape(b, shape=[4, -1]))
print(tf.reshape(b, shape=-1))
# 这些形状变换都只是改变了索引，张量在内存中的内容始终没有改变
# 张量中的轴的概念和用法，和NumPy数组是完全一样的，轴也可以是负数，表示从后向前索引

print('=================================================')
t = tf.range(24)
t = tf.reshape(t, shape=(2, 3, 4))
print(t.shape)

# tf.expand_dims增加一个维度，增加的维度长度为1，axis参数表示在序号为几的轴上增加维度
t1 = tf.expand_dims(t, 0)
t2 = tf.expand_dims(t, 1)
t3 = tf.expand_dims(t, axis=2)
t4 = tf.expand_dims(t, -1)
print(t1.shape, t2.shape, t3.shape, t4.shape)

print('-----------------------------------------------')
# tf.squeeze删除维度，只能删除长度为 1 的维度，省略时删除所有长度为1的维度
print(tf.squeeze(t1, 0))
print(tf.squeeze(t2))
# 增加维度和删除维度，只是改变了张量的视图，不会改变张量的存储

# tf.transpose交换维度，对二维张量交换维度，就是矩阵的转置
x = tf.constant([[1, 2, 3], [4, 5, 6]])
print(tf.transpose(x))
print('==================================================')
# 按照perm参数指定进行维度转换，转换前(2, 3, 4)，转换后(4, 2, 3)
print(t.shape, tf.transpose(t, perm=(2, 0, 1)).shape)

# tf.concat(tensors, axis)拼接张量：将多个张量在某个维度上合并，拼接并不会产生新的维度
# tensors：所有需要拼接的张量列表
# axis：指定在哪个轴上进行拼接
t1 = tf.reshape(tf.range(6), shape=(2, 3))
t2 = tf.reshape(tf.range(6), shape=(2, 3))
print(t1.shape, t2.shape)
# 在axis=0的轴上拼接，2+2=4
print(tf.concat((t1, t2), axis=0).shape)
# 在axis=1的轴上拼接，3+3=6
print(tf.concat((t1, t2), axis=1).shape)

# tf.split(value, num_or_size_splits, axis=0)分割张量：将一个张量拆分成多个张量，分割后维度不变
# value待分割张量，num_or_size_splits分割方案，axis指明分割的轴
# 分割方案：是一个数值时，表示等长分割，数值是切割的份数；是一个列表时，表示不等长切割，列表中是切割后每份的长度
# 例如2：分割成2个张量  [1:2:1]：就表示分割成3个张量，长度分别是1,2,1
t = tf.reshape(tf.range(24), shape=(4, 6))
# 在axis=0轴上等长分割成两份
print(tf.split(value=t, num_or_size_splits=2, axis=0))
# 在axis=1轴上按照1,3,2的长度分割
print(tf.split(value=t, num_or_size_splits=[1, 3, 2], axis=1))
# 图像的分割与拼接，改变了张量的视图，张量的存储顺序并没有改变。

print('=====================================================')
# tf.stack(values, axis)堆叠张量，在合并张量时，创建一个新的维度，和NumPy中堆叠函数的功能完全一样
a = tf.constant([1, 2, 3])
b = tf.constant([4, 5, 6])
print(a.shape)
print(tf.stack([a, b], axis=0))
print(tf.stack([a, b], axis=1))

print('=========================================================')
# tf.unstack(values, axis)是张量堆叠的逆运算，张量分解为多个张量，分解后得到的每个张量，和原来的张量相比，维数都少了一维
c = tf.constant([[1, 2, 3], [4, 5, 6]])
# 按照轴axis=0分解，原axis=0维度会消失，分解成两个shape=(3,)的张量
print(tf.unstack(c, axis=0))
# 分解成三个shape=(2,)的张量
print(tf.unstack(c, axis=1))

4、部分采样

import numpy as np
import tensorflow as tf
import pandas as pd

# 切片(起始位置:结束位置: 步长)
# 起始位置：结束位置，是前闭后开的，切片中不包含结束位置
# 起始位置、结束位置、步长都可以省略
# 步长可以是负数，这时起始位置的索引号，应该大于结束位置

a = tf.range(10)
# 当3个参数全部省略时，表示读取所有数据，步长为1
print(a[::])
# 从第一个元素开始，隔行采样，直到最后一个元素为止
print(a[::2])
# 读出所有的奇数
print(a[1::2])
# 从最后一个元素开始，逆序取出所有元素，步长是负数，起始位置的索引号，应该大于结束位置
print(a[::-1])
# 从最后一个元素开始，逆序取出间隔的元素
print(a[6:1:-2])

# 二维张量切片：维度之间用逗号隔开
TRAIN_URL = "http://download.tensorflow.org/data/iris_training.csv"
train_path = tf.keras.utils.get_file(TRAIN_URL.split("/")[-1], TRAIN_URL)
df_iris = pd.read_csv(train_path)
np_iris = np.array(df_iris)
iris = tf.convert_to_tensor(np_iris)
print(iris.shape)

# 读取第一个样本的所有列（包括属性和标记，前四列是属性，第五列是分类结果）
print(iris[0, :])
# 读取前5个样本的所有属性
print(iris[0:5, 0:4])
# 读取所有样本的第1个属性
print(iris[:, 0])
# 读取前10个样本的所有属性
print(iris[0:10, 0:4])

print('====================================================================')
data_url = "https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz"
download_path = tf.keras.utils.get_file("mnist.npz", data_url)
npz_data = np.load(download_path)
# 通过遍历查看mnist.npz中有哪些数据
for key in npz_data:
    print(key)
print(npz_data['x_train'].shape)  # (60000, 28, 28)
print(npz_data['y_train'].shape)  # (60000,)
# 牟琦老师课程中提到的mnist数据集指的是npz_data['x_train']这部分数据
data = npz_data['x_train']
# 第1张图片
print(data[0, ::, ::])
print(data[0, :, :])
# 为了更加简洁，两个冒号可以简写为一个冒号

# 前10张图片
print(data[0:10, :, :].shape)
# 前20张图片的所有的行，隔行采样
print(data[0:20, 0:28:2, ::].shape)
# 对所有的图片，隔行采样，并且隔列采样
print(data[:, 0:28:2, 0:28:2].shape)

# 数据提取：根据索引，抽取出没有规律的、特定的数据

# gather()函数：用一个索引列表，将给定张量中对应索引值的元素提取出来
# gather(params, indices)：params输入张量，indices索引值列表
a = tf.range(5)
# 从张量a中提取索引值分别为 0,2,3 的元素
print(tf.gather(a, indices=[0, 2, 3]))

# 对多维张量采样——gather()、gather_nd()函数
# gather(params, axis, indices)：axis说明在哪个轴上采样
# gather()函数一次对一个维度进行索引
a = tf.range(20)
b = tf.reshape(a, shape=[4, 5])
print(b)
# 对axis=0的轴采样（对行采样）
print(tf.gather(params=b, axis=0, indices=[0, 2, 3]))
# 对axis=1的轴采样（对列采样）
print(tf.gather(params=b, axis=1, indices=[0, 2, 3]))

# 同时采样多个点——gather_nd()函数
# 通过指定坐标，同时采样多个点，可以同时对多个维度进行索引
print(tf.gather_nd(b, [[0,0],[0,3],[2,1]]))
# 和使用3次索引的结果是一样的

# 选择采样维度
# 对前两维采样，表示去第i张图片的第n行
print(tf.gather_nd(data, [[0,5],[1,7],[4,1]]))
print('===============================================')
# 只对第一维采样，表示取到索引值为0,2,3的3张图片
print(tf.gather_nd(data,[[0],[2],[3]]))

5、张量运算

加减乘除运算、幂运算、对数运算、矩阵运算等

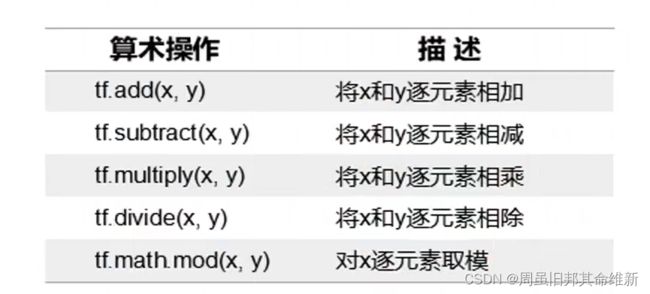
5.1 加减乘除

对两个张量逐元素的运算，并要求各个张量中元素的数据类型必须保持一致。

import numpy as np
import tensorflow as tf

# tf.add(x,y)加法
# tf.subtract(x,y)减法
# tf.multiply(x,y)乘法
# tf.divide(x,y)除法
# tf.math.mod(x,y)除法取余
a = tf.constant([0,1,6])
b = tf.constant([4,5,5])
print(tf.add(a, b))
print(tf.subtract(a,b))
print(tf.multiply(a,b))
print(tf.divide(a,b))
print(tf.math.mod(a,b))

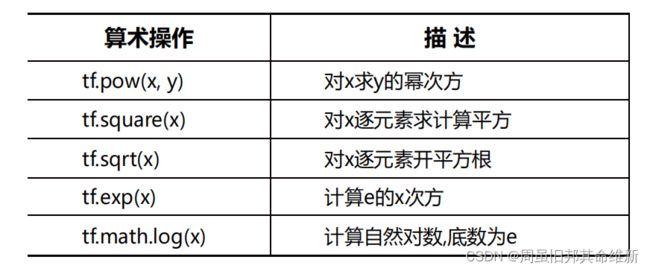
5.2 幂指对数运算

import numpy as np
import tensorflow as tf

# tf.pow(x,y)：对x求y的幂次方
a = tf.range(3)
b = tf.constant([1, 2, 3])
c = tf.constant([[1], [2], [3]])
print(tf.pow(a, 2))
# 求x中每一个元素的y次幂，如果y是张量，元素个数需要与x一致
print(tf.pow(a, b))
# 求x所有元素对c中每个元素都求一遍幂次方
print(tf.pow(a, c))
# y为小数时为开方运算，张量的元素必须是浮点数类型
d = tf.constant([1., 2., 3., 4.])
print(tf.pow(d, 0.5))

# 二维张量幂运算
x = tf.constant([[2, 3], [4, 4]])
y = tf.constant([[2, 1], [3, 3]])
# 对x中每个元素求对应y元素次方
print(tf.pow(x, y))

# tf.square专门的计算平方函数
x = tf.constant([3, 4, 5])
print(tf.square(x))
# tf.sqrt专门的计算平方根函数
x = tf.cast(x, dtype=float)
print(tf.sqrt(x))

# 自然指数和自然对数运算都要求张量的元素必须是浮点数类型
print(tf.exp(1.))
print(tf.exp(2.))

# 自然对数在math模块中
print(tf.math.log(0.5))
print(tf.math.log(7.3))
print(tf.math.log(100.))

# TensorFlow中只有以e为底的自然对数，没有提供以其他数值为底的对数运算函数，如果要计算其他底数的对数，可以通过对数的换底公式间接解决
x = tf.constant([256.])
y = tf.constant([2.])
print(tf.math.log(x) / tf.math.log(y))
x = tf.constant([[1., 9.], [16., 100.]])
y = tf.constant([[2., 3.], [4., 5.]])
print(tf.math.log(x) / tf.math.log(y))

5.3 其他运算

import numpy as np
import tensorflow as tf

x = tf.constant([3., 5., 6., 50])
y = tf.constant([1., 2., 3., 4.])
# tf.add
print(x + y)
# tf.subtract
print(x - y)
# tf.multiply
print(x * y)
# tf.truediv
print(x / y)
a = tf.constant([0,1,2,3])
b = 2
# tf.math.mod逐元素求余
print(x % b)
# tf.floordiv地板除法(整除)
print(x // y)
# tf.pow指数
print(x ** b)

# 广播机制（broadcasting），如果两个张量形状不同，两个张量最后一个维度的长度必须相等
# 一维张量和二维张量运算，即一维张量依次和二维张量第一个维度中的每个元素进行运算
z = tf.constant(np.arange(12).reshape(3,4), dtype=float)
print(x + z)
print('===================================')
# 一维张量和三维张量运算，即一维张量依次和三维张量前两维中的每个元素进行运算
z = tf.constant(np.arange(16).reshape(2,2,4),dtype=float)
print(z)
print(x + z)

# 当张量和一个数字进行运算时，会将这个数字值广播到张量的各个元素
print(x + b)

张量和NumPy数组之间的相互转换：

NumPy数组转化为张量：tf.constant()； tf.convert_to_tensor

张量转换为NumPy数组：Tensor.numpy()

import numpy as np
import tensorflow as tf

# 当张量和NumPy数组共同参与运算时:
# 执行TensorFlow操作，TensorFlow将自动的把NumPy数组转换为张量
# 执行NumPy操作，NumPy将自动的把张量转换为NumPy数组

nd = np.ones([2,2])
t = tf.multiply(nd, 35)
print(t)

print(np.add(nd, t))

# 使用运算符操作
# 只要操作数中有一个Tensor对象，就把所有的操作数都转化为张量，然后再进行运算。
print(nd + t)  # 操作数有tensor对象时运算符重载为张量加法
print(nd + 3)

5.4 向量乘法

元素乘法：tf.multiply(), *运算符

向量乘法：tf.matmul()，@运算符

import numpy as np
import tensorflow as tf

a = tf.constant(np.arange(6), shape=[2, 3])
b = tf.constant(np.arange(6), shape=(3, 2))
print(a)
print(b)

print(tf.matmul(a, b))
print(a @ b)

# 多维向量乘法
# 三维张量×二维张量：最后两维做向量乘法，高维采用广播机制

a = tf.random.normal([2, 3, 5])
b = tf.random.normal([5, 2])
# (3,5) * (5,2) -> (3,2) ->广播-> (2,3,2)
print(a @ b)

print('========================================')
# 多维向量乘法—— 三维张量×三维张量：最后两维做向量乘法，高维采用广播机制
a = tf.constant(np.arange(12), shape=[2, 2, 3])
b = tf.constant(np.arange(12), shape=[2, 3, 2])
print(a)
print(b)
print(a @ b)

# 多维向量乘法—— 四维张量×四维张量：最后两维做向量乘法，高维采用广播机制
a = tf.constant(np.arange(24), shape=[2, 2, 2, 3])
b = tf.constant(np.arange(24), shape=[2, 2, 3, 2])
print(a @ b)

5.5 常用数据统计函数

如果不指定axis参数，就表示求全局统计值。

import numpy as py
import tensorflow as tf

# 求和函数——tf.reduce_sum()

a = tf.constant([[1, 3, 4], [8, 9, 2]])
print(a)
print(tf.reduce_sum(a, axis=0))
print(tf.reduce_sum(a, axis=1))
# 没有指定axis参数时，默认全局求和
print(tf.reduce_sum(a))

# 求均值函数——tf.reduce_mean()

# 张量元素的数据类型是int32，因此求得的均值也是int32(一般希望均值是浮点数，因此创建张量时应当注意使用浮点类型)
print(tf.reduce_mean(a, axis=0))
# 如果创建张量默认使用了int32类型，可以将张量的数据类型转换为浮点数，再求均值
print(tf.reduce_mean(tf.cast(a, dtype=float), axis=0))
# 张量元素采用浮点数
b = tf.constant([[1., 3., 4.], [8., 9., 2.]])
# 得到浮点数的均值
print(tf.reduce_mean(b, axis=0))

# 求最大值、最小值函数——tf.reduce_max(), tf.reduce_min()

print(tf.reduce_max(a, axis=0))
print(tf.reduce_min(a, axis=0))
# 没有指定axis参数时，默认求全局最值
print(tf.reduce_max(a))

# 求最值的索引——tf.argmax(), tf.argmin()

print(tf.argmax(a, axis=0))
print(tf.argmax(a, axis=1))
print(tf.argmin(a, axis=0))
print(tf.argmin(a, axis=1))
# 没有指定axis参数时，默认axis=0
print(tf.argmax(a))