数据结构与算法详解——字符串匹配算法篇(附c++实现代码)
目录
-
- BF算法
- RK算法
- KMP算法
- BM算法有空再补
字符串匹配就是在主串A中查找模式串B,例如在主串abababc中查找模式串abc是否存在,记主串A的长度为n,模式串B的长度为m,n>=m。
BF算法
BF(Brute Force)算法,又叫暴力匹配算法或者朴素匹配算法,思路很简单:在主串中取前下标为[0,m-1]这m个字符的子串和模式串逐个字符逐个字符比较,如果完全一样就结束并返回下标;如果有不一样的,那么主串中的子串后移一位,主串中[1,m]这个子串和模式串继续比较,… ,主串中[n-m,n-1]这个子串和模式串继续比较。
主串中长度为m的子串有n-m+1个。
| 主串 | a | b | a | b | a | b | c |
|---|---|---|---|---|---|---|---|
| 模式串 | a | b | c |
| 主串 | a | b | a | b | a | b | c |
|---|---|---|---|---|---|---|---|
| 模式串 | a | b | c |
| 主串 | a | b | a | b | a | b | c |
|---|---|---|---|---|---|---|---|
| 模式串 | a | b | c |
| 主串 | a | b | a | b | a | b | c |
|---|---|---|---|---|---|---|---|
| 模式串 | a | b | c |
| 主串 | a | b | a | b | a | b | c |
|---|---|---|---|---|---|---|---|
| 模式串 | a | b | c |
int BF(std::string &s,std::string &pattern) {
int n = s.length(), m = pattern.length();
for (int i = 0; i < n-m+1; i++) {
int j = 0;
for (; j < m; j++) {
if (s[i + j] != pattern[j])
break;
}
if(j==m)
return i; //匹配到了,返回主串中的下标
}
return -1; //匹配不到
}
最坏的情况下,在第一个for循环里,i 从0到n-m走满共n-m+1次,第二个for循环里,j 从0到m-1走满共m次,因此最坏的情况下时间复杂度为O(n*m),举个例子,在bbbbbbf中查找bf,所有n-m+1个子串都要走完,并且每次和模式串比较都要比较m次,总共比较n-m+1次。
BF算法最大的优点就是简单,代码不容易出错,在主串和模式串的长度都不大的时候还是比较实用的。
RK算法
RK(Rabin-Karp)算法,是用两个发明者的名字命名的。思路也比较简单:对主串中n-m+1个子串求哈希值,模式串也求哈希值,然后比较子串的哈希值和模式串的哈希值,如果不相等证明不匹配,如果相等就匹配(在没有哈希冲突的情况,冲突的情况后面会讲)。
这个算法对哈希函数的设计要求会高一点,当然最好就不存在哈希冲突,就会比较简单,相等就匹配,不相等就不匹配。
来看看这样一个设计:假设主串和模式串只有a-j这10个字母,我们可以直接将字符串映射成整数(a-j对应十进制0-9),例如bcd我们可以直接映射成bcd=1*10*10+2*10+3=123,这样就不存在哈希冲突了。那如果现在是a-z这26个字母,我们可以用同样的思路,但是使用26进制,a-z对应0-25:例如bcd=1*26*26+2*26+3=731。
这个哈希函数是有规律的,当前子串的哈希值hash[i]是可以根据上一个子串的哈希值hash[i-1]计算得到,来看看下面这个例子:

上面的子串aba的起始坐标为i-1,哈希值为hash[i-1],下面子串bab的起始坐标为i,哈希值为hash[i],我们知道两个子串中都有ba,但是下面的ba映射成的值要比上面的ba要大26倍,因为所在的位置不一样,下面的ba在最高位和第二位,下面的ba在第二位和第三位,那么我们将hash[i-1]乘26,上下子串ba的hash值都相同了,然后再减去上面子串的最高位a(注意此时的a也是乘多了个26的),最后加上下面子串的末尾的b即可。最终的计算结果就同上图中的计算一样,注意蓝色框框的m即可,是m而不是m-1,因为hash[i-1]乘了26。
//假设哈希值不会溢出int的范围
int RK(std::string& s, std::string& pattern) {
int n = s.length(), m = pattern.length();
int p = pow(26, m); //26的m次方
int* hash = new int[n - m + 1];
hash[0] = s[0] - 'a';
int hash_pattern = pattern[0] - 'a';
for (int i = 1; i < m; i++) { //求第一个子串的哈希值hash[0]和模式串的哈希值hash_pattern
hash[0] = hash[0] * 26 + s[i] - 'a';
hash_pattern = hash_pattern * 26 + pattern[i] - 'a';
}
for (int i = 1; i < n - m + 1; i++) //根据前一个子串的哈希值求所有的子串的哈希值,代入上图的公式
hash[i] = 26 * hash[i - 1] - (s[i - 1] - 'a') * p + (s[i + m - 1] - 'a');
for (int i = 0; i < n - m + 1; i++) //比较模式串的哈希值hash_pattern和每个子串的哈希值
if (hash[i] == hash_pattern) //相同即匹配
return i;
return -1; //不匹配
}
int main() {
std::string a = "abababc";
std::string p = "abc";
std::cout << RK(a, p) << std::endl;
}
遍历一次主串就可以求出所有子串的哈希值了,求一个子串的哈希值时间复杂度可以看做O(1),求所有子串的哈希值的时间复杂度为O(n)。模式串和子串的哈希值比较时间复杂度为O(1),共有n-m+1个子串即比较n-m+1次,所以时间复杂度为O(n)。所以RK算法的时间复杂度为O(n)。
如果模式串的长度m太大,字符不止26个字母,我们上面设计的算法可能会溢出整型数据的范围,我们也可以设计别的哈希函数:例如每种字符对应一个小质数,然后将所有字符对应的质数相加得到哈希值,这样算出来的哈希值会比较小,基本不会溢出,但是可能会造成哈希冲突。
存在哈希冲突的情况下,我们对比子串的哈希值和模式串的哈希值,如果不相等还是证明两个串不匹配;如果相等,由于存在哈希冲突的情况,我们还不能判定子串和模式串相等,还需要逐个字符进行比较,如果每个字符都相同,才能证明匹配。
在极端的情况下,存在大量哈希冲突,RK算法会退化BF算法,时间复杂度为O(n*m)。
KMP算法
KMP算法是一种改进的字符串匹配算法,由D.E.Knuth,J.H.Morris和V.R.Pratt提出的,也是由这三位作者的名字进行命名的,用i 遍历主串,j 遍历模式串,主要的思想就是主串的 i 不回溯,模式串的 j 回溯到某个位置k,使得模式串的[0,k-1]的位置和主串[i-k,i-1]的位置直接匹配。来看看下面的例子:

这个例子中,我们一直比较s[i]和pattern[j]的值,当i=j=4的时候也就是上图中的红色框框的时候,s[i]!=pattern[j],此时如果按照BF算法,i 回溯到1,j 回溯到0继续比对,但其实是不必要的,因为i 回溯到1,s[i]=‘b’,而j 回溯到0,pattern[j]=‘a’,很明显是不匹配的;来看看KMP算法的做法:主串不回溯也就是 i 不动,j 回溯到 k的位置,使得模式串的[0,k-1]的位置和主串[i-k,i-1]的位置直接匹配(下图中 j 前的a和 i 前的a匹配,即蓝色框框的部分直接匹配):
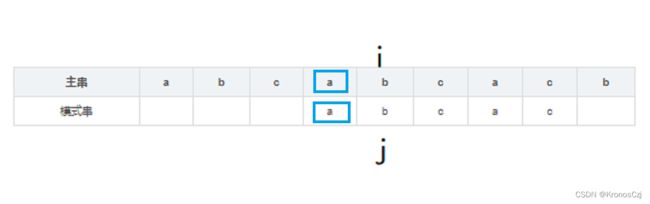
那现在问题就变成了位置k的确定。前面说到k的位置要满足:模式串的[0,k-1]的位置和主串[i-k,i-1]的位置直接匹配,也就是第二幅图中蓝色框框的部分匹配。那再来看看第一幅图中的两个绿色框框,可以发现模式串的[j-k,j-1]和主串的[i-k,i-1]部分相等,整理得到:
pattern[0]~pattern[k-1] = s[i-k]~s[i-1]
pattern[j-k]~pattern[j-1] = s[i-k]~s[i-1]
两个等式右边部分都相等,所以我们可以得到两个等式左边部分相等:
pattern[0]~pattern[k-1] =pattern[j-k]~pattern[j-1]

其实就是上面这幅图中3个绿色的框框,整个道理也很简单:就是因为i 和 j前的a相等,而j 前的a 和 k前的a 相等,所以我们下次回溯的时候,就用k 前的a 对准 i 前的a,有机会可以匹配成功,而省略了BF算法中的多次不必要的回溯和比较。
我们现在可以知道k的位置是由模式串本身来确定的,和主串无关:pattern[0]~pattern[k-1] =pattern[j-k]~pattern[j-1],也就是说模式串中每一个字符pattern[j]都对应着一个k值,这个k值只与模式串有关,我们用next[j]表示pattern[j]对应的k值,next数组的求解就是KMP算法的关键。
next[j]就是模式串[0,j-1]的子串中真前缀和真后缀的最长可匹配长度,下面举一个例子(模式串为ababc):
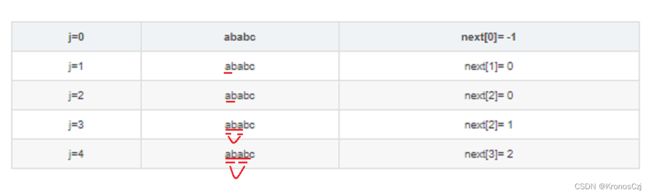
j=0时,next[0]=-1表示不存在,因为当j=0的时候,j-1=-1是非法下标。
j=1时,[0,j-1]的子串只有一个a,没有真前缀和真后缀(因为真前缀真后缀不能包含自身),此时next[1]=0。
j=2时,[0,j-1]的子串为ab,此时【真前缀为a,真后缀为b】,可最长匹配长度为0,所以next[2]=0;
j=3时,[0,j-1]的子串为aba,此时【真前缀为a,真后缀为a】,还有一种组合【真前缀为ab,真后缀为ba】,第一个组合的匹配长度为1,第二个组合的匹配长度为0,最长匹配长度为1,所以next[3]=1。
j=4时,[0,j-1]的子串为abab,此时的组合有:【真前缀为a,真后缀为b】,【真前缀为ab,真后缀为ab】,【真前缀为aba,真后缀为bab】,匹配长度分别为0,2,0,最长匹配长度为2,所以next[4]=2。
上面这种方法只是我们用人脑计算真前缀和真后缀的最长可匹配长度,那要是让计算机来如何计算呢?我们贴出代码,再结合代码进行解释:
void getnext(std::string &pattern, int next[]) { //next的长度为m
int m = pattern.length();
int k = -1 ,j = 0 ;
next[0] = -1;
while (j < m) {
if (k == -1 || pattern[j] == pattern[k])
next[++j] = ++k;
else
k = next[k];
}
}
前三行代码应该没啥问题,k和j相当于两个快慢指针,k用来找真前缀,j用来找真后缀。next[j]=k要满足的关系也正如我们前面提到的:
pattern[0]~pattern[k-1] =pattern[j-k]~pattern[j-1]
接下来是while循环,j的另一个作用是用来遍历模式串的,所以循环的条件是j
再来看看为什么要判断k==-1,首先k初始化为-1,因为j是从0开始的,j是快指针,k是慢指针,所以k要从-1开始。if分支里要访问pattern[k]的值,k为-1的时候是非法下标;其次在else语句中,k = next[k]导致了k是会往前走的(也就是k会变小),有可能k回退到next[0]的时候又会变为-1了,所以在访问pattern[k]的时候又会是非法下标。综上所述,判断k==-1是为了保证访问pattern[k]时数组下标合法。
整段代码的关键就在于else分支的k = next[k](也就是k!=-1且pattern[j] != pattern[k]),也是最难懂的地方,让我们来看个例子:
如图,现在已知next[13]=6,求next[14],所以两个橙色框框内长度为6的真前缀和真后缀是相同的(也就是0和7相同,1和8相同,2和9相同以此类推…最后5和12相同);假如现在走if分支:pattern[k]==pattern[j]即pattern[6]==pattern[13]的话,那么执行next[++j] = ++k即next[14]=7,这个应该没啥问题。
那如果走的else分支呢?pattern[k]!=pattern[j]即pattern[6]!=pattern[13]:k = next[k]
现在假设next[k]=i,如图所示,那么代表(0和1的绿框的两个真前缀和4和5的蓝框的后前缀相同),但是前面说过两个橙色框相同,可以推出两个绿框相同,两个篮筐也相同,最终推导出两个篮筐和两个绿框总共4个框框里面的字符串都相同(即0、4,、7、11相同;1、5、8、12相同);我们的目的主要是为了证明(0和1的绿框 与 11和12的蓝框相同),那么现在只需比较pattern[j]是否等于pattern[i],如果相等next[++j]=++i也即next[14]=3。而我们为了逻辑统一,将 i 赋值给k,即k=next[k],那么又可以回到if的分支和else的分支进行判断了。
如果还不明白为什么k要初始化为1,代码也可以这样写:k初始化为0,j初始化为1,如果pattern[j] == pattern[k]那么next[2]=1这里应该没问题,因为k指向真前缀,j指向真后缀。但是仍要判断k==-1,因为next[0]=-1,k回退时有可能还是会出现-1的情况。其次 next[1]=0这里可能会溢出,因为m=1的时候next数组的长度也只有1。我们可以将next[1]也并入下面的逻辑,也就是k从-1开始,j从0开始,同样的if else逻辑也可以计算出next[1]=0,所以我们不采取下面这种写法,而采用上面的写法。
void getnext(std::string &pattern, int next[]) { //next的长度为m
int m = pattern.length();
int j = 1, k = 0;
next[0] = -1;
next[1] = 0; //模式串的长度m可能只有1,所以这里有可能会溢出
while (j < m) {
if (k == -1 || pattern[j] == pattern[k]) //next[0]=-1,k回退时有可能还是会出现-1的情况
next[++j] = ++k;
else
k = next[k];
}
}
在构建完next数组后,剩下的部分就简单了:
int KMP(std::string& s, std::string& pattern) {
int n = s.length(), m = pattern.length(), j = 0, i = 0;
int* next = new int[m];
getnext(pattern, next);
while (i < n && j < m) {
if (j == -1 || s[i] == pattern[j]) {
++i;
++j;
}
else
j = next[j];
}
if (j == m) //j走完整个pattern证明匹配成功,也会退出while循环
return i - m; //返回匹配开始的位置,这里return i-j和return i-m是一样的,因为j==m
return -1;
}
前面说过,kmp算法主串不回溯,也就是i是不回溯的,一直往上加遍历主串,如果j==-1或者s[i] == pattern[j]时,i和j分别自加,准备下一个字符的比较,否则j回溯到next[j]的位置,回溯后pattern[0]~pattern[j-1] = s[i-j]~s[i-1],也就是说j前面的字符串和主串是已经匹配的了,只需要继续比较pattern[j]和s[i]。
while循环结束的情况有:i==n或者j==m或者(i==n且j==m),只要j==m就证明匹配成功,因为j走完了整个pattern,说明每个pattern的字符在主串中都能匹配上。
完整代码:
void getnext(std::string &pattern, int next[]) { //next的长度为m
int m = pattern.length();
int j = 0, k = -1;
next[0] = -1;
while (j < m) {
if (k == -1 || pattern[j] == pattern[k])
next[++j] = ++k;
else
k = next[k];
}
}
int KMP(std::string& s, std::string& pattern) {
int n = s.length(), m = pattern.length(), j = 0, i = 0;
int* next = new int[m];
getnext(pattern, next);
while (i < n && j < m) {
if (j == -1 || s[i] == pattern[j]) {
++i;
++j;
}
else
j = next[j];
}
if (j == m) //j走完整个pattern证明匹配成功,也会退出while循环
return i - m; //返回匹配开始的位置,这里return i-j和return i-m是一样的,因为j==m
return -1;
}
int main() {
std::string a = "abababc";
std::string p = "abc";
std::cout << KMP(a, p) << std::endl;
}
KMP算法使用了额外的next数组,长度是pattern的长度m,所以空间复杂度是O(m)。
getnext函数的时间复杂度为O(m),KMP函数中的while循环时间复杂度为O(n),因此KMP算法的时间复杂度为O(m+n)。