速成! | 遗传算法详解及其MATLAB实现
00目录
遗传算法基本思想
算法步骤
问题导入
MATLAB程序实现
遗传算法改进策略
01遗传算法概述
遗传算法**(genetic algorithm,GA)**是-种进化算法,其基本原理是仿效生物界中的“物竞天择、适者生存”的演化法则。
遗传算法提供了求解非线性规划的通用框架，其将问题参数编码为染色体，生成初始种群，再利用迭代的方式进行选择、交叉以及变异等运算来交换种群中染色体的信息,最终生成符合优化目标的染色体。
在遗传算法中,染色体对应的是数据或数组,通常是由一维的串结构数据来表示,串上各个位置对应基因的取值。其核心内容包括染色体编码、初始种群设定、适应度函数设计、遗传操作设计等。
02算法实现步骤
算法主要步骤如上图所示，下面将对每一步作简单介绍，大家稍作了解即可。
- 编码
编码是应用遗传算法时要解决的首要问题，也是设计遗传算法时的一个关键步骤。其影响遗传算法的交叉、选择、变异操作，很大程度上影响着遗传算法的效率。现有的编码方式主要有二进制编码、实数编码等。 - 初始群体的生成
随机产生N个初始编码串,每个编码串称为一个个体,N个个体构成了一个群体。GA以这N个编码串作为初始点开始进化。 - 适应度评估
适应度表明个体或解的优劣性。不同的问题，相应的适应度函数的设计也不同。 - 选择
选择的目的是为了从当前群体中选出优良的个体,使它们有机会作为父代为下一代繁殖子孙。遗传算法通过选择过程体现这一思想,进行选择的原则是适应性强的个体为下一代贡献一个或多个后代的概率大。选择体现了达尔文的适者生存原则。 - 交叉
交叉操作是遗传算法中最主要的遗传操作。通过交叉操作可以得到新一代个体,新个体组合了其父辈个体的特性。交叉体现了信息交换的思想。 - 变异
变异首先在群体中随机选择一个个体,对于选中的个体以一定的概率随机地改变编码串中某个串的值。同生物界一样,GA中变异发生的概率很低,通常取值很小。
03 问题导入
3.1问题描述
为便于大家对遗传算法有深入的理解，这里引入一个简单的二元函数的案例
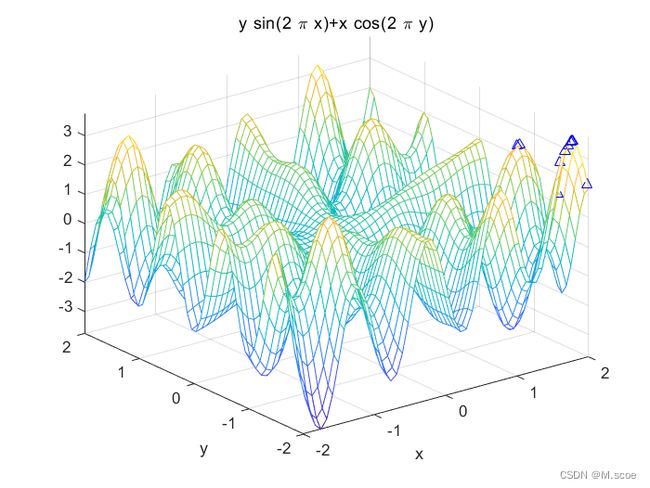
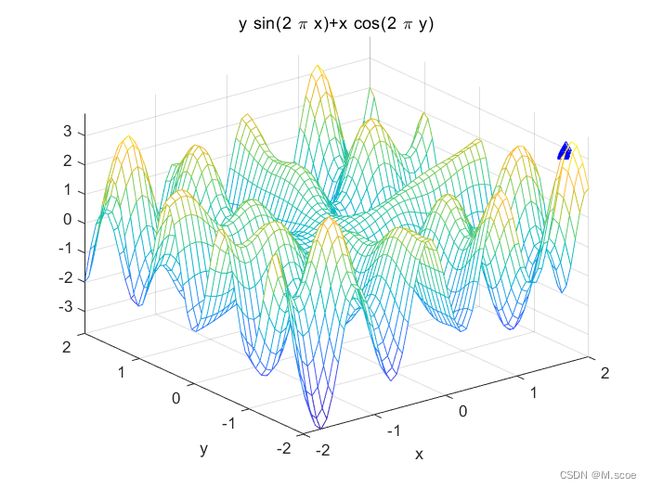
f(x,y)=xcos(2Πy)+ysin(2Πx) ,x∈[-2,2],y∈[-2,2]
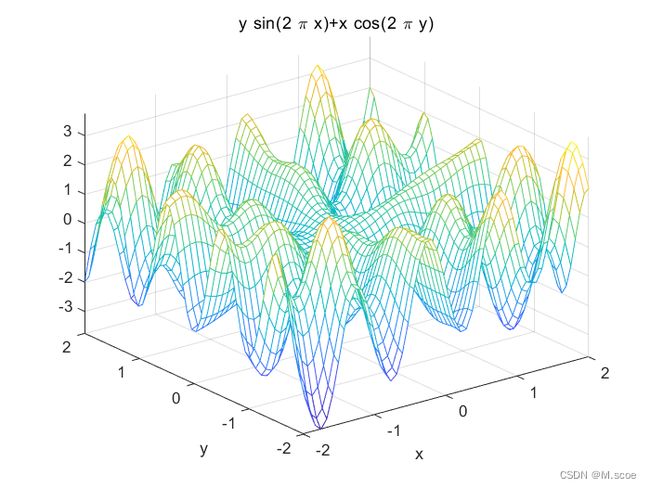可见，这个二元函数是典型的多峰函数，这类多峰函数优化问题在实际应用中大量存在，因此本文以此为例对遗传算法进行介绍。
3.2解题思路及步骤
将自变量在给定范围内进行编码，得到种群编码,按照所选择的适应度函数并通过遗传算法中的选择、交叉和变异操作对个体进行筛选和进化,使适应度值大的个体被保留,小的个体被淘汰，新的群体继承了上一代的信息,又优于上一代,这样反复循环,直至满足条件,最后留下来的个体集中分布在最优解周围,筛选出其中最优的个体作为问题的解。
04MATLAB程序实现
采用遗传算法进行优化，有两个可选方案，分别是谢菲尔德大学的遗传算法的工具箱和自编代码，下面将一一介绍。
4.1谢菲尔德遗传算法工具箱
4.1.1工具箱简介
谢菲尔德（Sheffield）遗传算法工具箱是英国谢菲尔德大学开发的遗传算法工具箱，能够为遗传算法研究者和初次使用遗传算法的用户提供了广泛多样的实用函数。但该工具箱不支持多目标优化。
4.1.2工具箱添加
（1）将工具箱文件夹放在matlab的toolbox中,我的路径是C:\Program Files\Polyspace\R2020a\toolbox。
（工具箱获取方式放在文章末尾）。
（2）将工具箱添加入MATLAB的搜索路径，这里可以通过addpath命令添加，如
代码如下（示例）：
addpath(genpath('C:\Program Files\Polyspace\R2020a\toolbox\gatbx-toolbox'));
输入上述命令后即完成了添加。
（3）检查安装是否成功
使用ver函数查看该工具箱相关信息，如
ver('gatbx')
若返回以上信息 则表示安装成功。
4.1.3工具箱函数结构
该工具箱主要函数如下表所列
具体各个函数的使用方法，感兴趣的同学可以通过doc xxx或是《MATLAB遗传算法工具箱及应用》这本书进行参照学习。
4.1.4工具箱代码实现
%% 多元函数优化
clc
clear all
close all
%% 画出函数图
figure(1);
lbx=-2;ubx=2; %函数自变量x范围【-2,2】
lby=-2;uby=2; %函数自变量y范围【-2,2】
ezmesh('y*sin(2*pi*x)+x*cos(2*pi*y)',[lbx,ubx,lby,uby],50); %画出函数曲线
hold on;
syms x ;%符号数学计算
y=(2+x)*exp(1/x);
fplot(y,[2,100]);
%% 定义遗传算法参数
NIND=40; %个体数目
MAXGEN=50; %最大遗传代数
PRECI=20; %变量的二进制位数
GGAP=0.95; %代沟
px=0.7; %交叉概率
pm=0.01; %变异概率
trace=zeros(3,MAXGEN); %寻优结果的初始值
FieldD=[PRECI PRECI;lbx lby;ubx uby;1 1;0 0;1 1;1 1]; %区域描述器
Chrom=crtbp(NIND,PRECI*2); %初始种群
%% 优化
gen=0; %代计数器
XY=bs2rv(Chrom,FieldD); %计算初始种群的十进制转换
X=XY(:,1);Y=XY(:,2);
ObjV=Y.*sin(2*pi*X)+X.*cos(2*pi*Y); %计算目标函数值
while gen<MAXGEN
FitnV=ranking(-ObjV); %分配适应度值
SelCh=select('sus',Chrom,FitnV,GGAP); %选择
SelCh=recombin('xovsp',SelCh,px); %重组
SelCh=mut(SelCh,pm); %变异
XY=bs2rv(SelCh,FieldD); %子代个体的十进制转换
X=XY(:,1);Y=XY(:,2);
ObjVSel=Y.*sin(2*pi*X)+X.*cos(2*pi*Y); %计算子代的目标函数值
[Chrom,ObjV]=reins(Chrom,SelCh,1,1,ObjV,ObjVSel); %重插入子代到父代，得到新种群
XY=bs2rv(Chrom,FieldD);
gen=gen+1; %代计数器增加
%获取每代的最优解及其序号，Y为最优解,I为个体的序号
[Y,I]=max(ObjV);
trace(1:2,gen)=XY(I,:); %记下每代的最优值
trace(3,gen)=Y; %记下每代的最优值
end
plot3(trace(1,:),trace(2,:),trace(3,:),'b^'); %画出每代的最优点
grid on;
plot3(XY(:,1),XY(:,2),ObjV,'b^'); %画出最后一代的种群
hold off
4.2自编代码的程序实现
%% 清空环境
clc
clear
%% 遗传算法参数
maxgen=40; %进化代数
sizepop=100; %种群规模
pcross=[0.7]; %交叉概率
pmutation=[0.01]; %变异概率
lenchrom=[1 1]; %变量字串长度
bound=[-2 2;-2 2]; %变量范围
%% 个体初始化
individuals=struct('fitness',zeros(1,sizepop), 'chrom',[]); %种群结构体
avgfitness=[]; %种群平均适应度
bestfitness=[]; %种群最佳适应度
bestchrom=[]; %适应度最好染色体
% 初始化种群
for i=1:sizepop
individuals.chrom(i,:)=Code(lenchrom,bound); %随机产生个体
x=individuals.chrom(i,:);
individuals.fitness(i)=fun(x); %个体适应度
end
%找最好的染色体
[bestfitness bestindex]=max(individuals.fitness);
bestchrom=individuals.chrom(bestindex,:); %最好的染色体
avgfitness=sum(individuals.fitness)/sizepop; %染色体的平均适应度
% 记录每一代进化中最好的适应度和平均适应度
trace=[];
chrom = [];
%% 进化开始
for i=1:maxgen
% 选择操作
individuals=Select(individuals,sizepop);
avgfitness=sum(individuals.fitness)/sizepop;
% 交叉操作
individuals.chrom=Cross(pcross,lenchrom,individuals.chrom,sizepop,bound);
% 变异操作
individuals.chrom=Mutation(pmutation,lenchrom,individuals.chrom,sizepop,[i maxgen],bound);
% 计算适应度
for j=1:sizepop
x=individuals.chrom(j,:);
individuals.fitness(j)=fun(x);
end
%找到最小和最大适应度的染色体及它们在种群中的位置
[newbestfitness,newbestindex]=max(individuals.fitness);
[worestfitness,worestindex]=min(individuals.fitness);
% 代替上一次进化中最好的染色体
if bestfitness<newbestfitness
bestfitness=newbestfitness;
bestchrom=individuals.chrom(newbestindex,:);
end
individuals.chrom(worestindex,:)=bestchrom;
individuals.fitness(worestindex)=bestfitness;
avgfitness=sum(individuals.fitness)/sizepop;
chrom = [chrom;bestchrom];
trace=[trace;avgfitness bestfitness]; %记录每一代进化中最好的适应度和平均适应度
end
%进化结束
4.3结果分析
4.3.1工具箱优化结果
最优解：x=1.763,y=-1.9998,z=3.7561
4.3.2自编代码优化结果
最优解：x=-1.814,y=1.414,z=3.723
可以看出，两种方案的结果大致相似，但工具箱的方法的解种群较之于自编代码的更加多样，因此也更不容易陷入局部最优中。
05遗传算法的改进策略
可以看出，两种方案的结果大致相似，但工具箱的方法的解种群较之于自编代码的更加多样，因此也更不容易陷入局部最优中。
本文完整代码及工具箱链接：
链接：https://pan.baidu.com/s/1QhxfVhCCf6NLNm-FFxJlNA
提取码：1111
感兴趣的朋友可以关注公众号：川子凯 ，作者不定时分享各类代码/日常