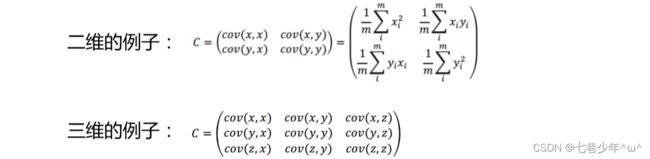第十章.主成分分析PCA(Principal Component Analysis)

第十章.主成分分析(PCA)

10.1 主成分分析

1.主成分分析的作用：降维

1).数据压缩2D-1D

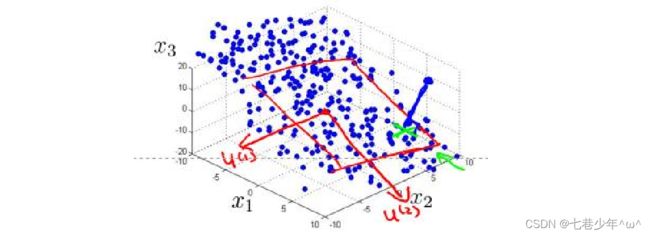
2).数据压缩3D-2D

3).数据可视化

• 多特征的数据
  
• 将多特征的数据降维为2维数据（不是挑选两个特征）
  
• 用平面坐标系表示出来
  

2.降为分析

1).找到数据最重要的方向（方差最大的方向）

2).第一个主成分就是从数据差异性最大(方差最大)的方向提取出来的，第二个主成分则来自于数据差异性次大的方向，并且要与第一个主成分方向正交。

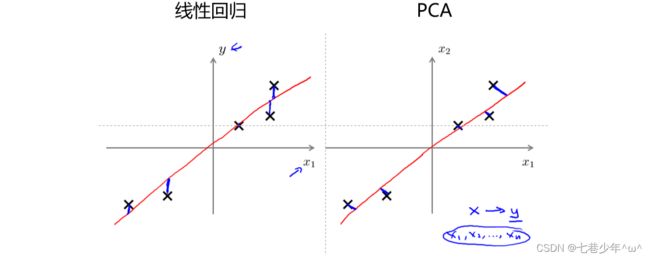
3.PCA不是线性回归

• 线性回归会使用最小二乘法求代价函数的最小值，样本点到红色直线的竖直距离，PCA是样本点到红色直线的垂线距离
  

4.PCA算法流程

①.数据预处理：中心化−`。

②.求样本的协方差矩阵(1/m)

③.对协方差(1/m)矩阵做特征值分解。

④.选出最大的k个特征值对应的k个特征向量。

⑤.将原始数据投影到选取的特征向量上。

⑥.输出投影后的数据集。

5.协方差

1).方差

方差是描述一个数据的离散程度：

2).协方差

协方差是描述两个数据的相关性，接近1就是正相关， 接近-1就是负相关，接近0就是不相关。

3).协方差矩阵

• 协方差只能处理二维问题，那维数多了自然需要计算多个协方差，我们可以使用矩阵来组织这些 数据。 协方差矩阵是一个对称的矩阵，而且对角线是各个维度 的方差。

• n个特征，m个样本->n行m列
  
• n行m列乘m行n列->n行n列
  
• result
  

6.特征值与特征向量

通过数据集的协方差矩阵及其特征值分析，我们可以得到协方差矩阵的特征向量和特征值。我们需要保留k个维度的特征就选取最大的k个特征值。

7.示例

1).示例1：将二维数据降维到一维数据

①.代码实现

import numpy as np
import matplotlib.pyplot as plt


# 数据中心化
def zeroMean(data):
    mean = np.mean(data, axis=0)  # 按列求平均，即各个特征的均值
    norm = data - mean
    return norm, mean


def PCA(data, k):
    # 1.数据中心化
    norm, mean = zeroMean(data)

    # 2.样本的协方差矩阵
    covMat = np.cov(norm, rowvar=0)  # rowvar=0:一行数据代表一个样本

    # 3.对协方差矩阵做特征值和特征向量分解
    eigVals, eigVects = np.linalg.eig(np.mat(covMat))

    # 4.选出最大的k个特征值对应的k个特征向量。
    eigVals_sort = np.argsort(eigVals)
    n_eigVals = eigVals_sort[-1:-(k + 1):-1]  # 最大的k个特征值的下标
    n_eigVects = eigVects[:, n_eigVals]  # 对应的k个特征向量

    # 5.将原始数据投影到选取的特征向量上。
    lowData = norm * n_eigVects  # 低维特征空间的数据
    reconMat = (lowData * n_eigVects.T) + mean  # 利用低维数据来重构数据

    return lowData, reconMat


# 加载数据
data = np.genfromtxt('F:\\data.csv', delimiter=',')

# 原始数据点
x_data = data[:, 0]
y_data = data[:, 1]
plt.scatter(x_data, y_data, c='b')

# 重构后的数据点
k = 1  # 数据降到k维
lowData, reconMat = PCA(data, k)

# 6.重构数据
x_dstdata = np.array(reconMat)[:, 0]
y_dstdata = np.array(reconMat)[:, 1]
plt.scatter(x_dstdata, y_dstdata, c='r')

plt.show()

②.结果展示

2).示例2：手写数字识别降维可视化

①.代码实现

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split

# 加载数据
digits = load_digits()

# 数据
x_data = digits.data

# 标签
t_data = digits.target

# 数据分割：训练数据和测试数据
x_train, x_test, t_train, t_test = train_test_split(x_data, t_data)


# 数据中心化
def zeroMean(data):
    mean = np.mean(data, axis=0)  # 按列
    norm = data - mean
    return norm, mean


# PCA
def PCA(data, k):
    # 1.数据中心化
    norm, mean = zeroMean(data)

    # 2.样本的协方差矩阵
    covMat = np.cov(norm, rowvar=0)

    # 3.对协方差矩阵做特征值和特征向量分解
    eig_vals, eig_vects = np.linalg.eig(np.mat(covMat))

    # 4.选出最大的k个特征值对应的k个特征向量
    eig_vals_sort = np.argsort(eig_vals)
    n_eig_vals = eig_vals_sort[-1:-(k + 1):-1]
    n_eig_vects = eig_vects[:, n_eig_vals]

    # 5.将原始数据投影到选取的特征向量上
    lowData = norm * n_eig_vects
    reconMat = (lowData * n_eig_vects.T) + mean

    return lowData, reconMat

fig = plt.figure(figsize=(6, 3))

k = 2
# 降维数据
lowData, reconMat = PCA(x_data, k)
x_dstdata = np.array(lowData)[:, 0]
y_dstdata = np.array(lowData)[:, 1]
print(x_dstdata)
print(y_dstdata)
fig.add_subplot(121)
plt.scatter(x_dstdata, y_dstdata, c=t_data)
plt.title('2D')

k = 3
# 降维数据
lowData, reconMat = PCA(x_data, k)
x_dstdata = np.array(lowData)[:, 0]
y_dstdata = np.array(lowData)[:, 1]
z_dstdata = np.array(lowData)[:, 2]
ax = fig.add_subplot(122, projection='3d')
ax.scatter(x_dstdata, y_dstdata, z_dstdata, c=t_data, s=10)
plt.title('3D')

plt.show()

②.结果展示