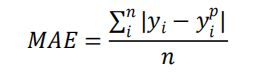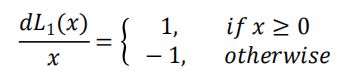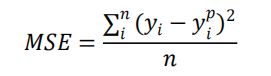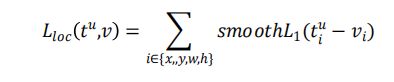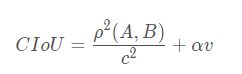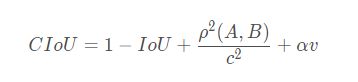AI大视觉（十五） | 损失函数进化史：MSE、IOU、GIOU、DIOU、CIOU、EIOU

本文来自公众号“AI大道理”。

这里既有AI，又有生活大道理，无数渺小的思考填满了一生。

目标检测任务的损失函数由两部分构成：Classification Loss和Bounding Box Regeression Loss。

Smooth L1 Loss

L1 Loss（Mean Absolute Error，MAE）

平均绝对误差（MAE）是一种用于回归模型的损失函数。

MAE 是目标变量和预测变量之间绝对差值之和，因此它衡量的是一组预测值中的平均误差大小，而不考虑它们的方向，范围为 0~∞。

MAE公式：

MAE导数：

MAE Loss主要问题：
导数为常数，在 Loss 函数最小值处容易震荡，导致难以收敛到最优值。

L2 Loss（Mean Squared Error，MSE）

均方误差（MSE）是最常用的回归损失函数，它是目标变量和预测值的差值平方和。

MSE公式：

MSE导数：

MSE Loss主要问题：
导数变化，不稳定，尤其是在早期阶段（损失越大，导数越大），随着导数越来越小， 训练速度变得越来越慢。

以往的目标检测模型（比如YOLO V3)等，都是直接根据预测框和真实框的中心点坐标以及宽高信息设定MSE(均方误差）损失函数或者BCE损失函数的。

YOLO V3的损失函数主要分为三部分，分别为：

• bounding box regression损失

• 置信度损失

• 分类损失

Smooth L1 Loss

Smooth L1 Loss 结合了 L1 和 L2 的优点：早期使用 L1，梯度稳定，快速收敛，后期使用 L2，逐渐收敛到最优解。

Smooth L1作为目标检测回归Loss的缺点：

1）坐标分别计算：x、y、w、h分别回归，当成4个不同的对象处理。

bbox的4个部分应该是作为一个整体讨论，但是被独立看待了。

2）不同的预测bbox具有相同的损失：把x、y、w、h独立看待，4个部分产生不同的loss会回归出不同的预测框，但是如果4个部分的总体loss相同，预测框该如何选取。

3）模型在训练过程中更偏向于尺寸更大的物体。

 IOU Loss

进化一：Smooth L1系列变量相互独立且不具有尺度不变性，改进为IOU。

IoU Loss 将 4 个点构成的 bbox 看成一个整体进行回归。

IOU Loss的定义是先求出预测框和真实框之间的交集和并集之比，再求负对数，但是在实际使用中我们常常将IOU Loss写成1-IOU。

如果两个框重合则交并比等于1，Loss为0说明重合度非常高。

IOU算法流程如下：

IoU Loss的优点：

1）它可以反映预测光与真实框的检测效果。
2）具有尺度不变性，也就是对尺度不敏感（scale invariant），满足非负性、同一性、对称性、三角不变性。

IoU Loss存在的问题：

IOU Loss虽然解决了Smooth L1系列变量相互独立和不具有尺度不变性的两大问题，但是它也存在两个问题：

1）预测框和真实框不相交时，不能反映出两个框的距离的远近。

根据IOU定义loss等于0，没有梯度的回传无法进一步学习训练。

2）预测框和真实框无法反映重合度大小。

借用一张图来说，三者具有相同的IOU，但是不能反映两个框是如何相交的，从直观上感觉第三种重合方式是最差的。

无法优化两个框不相交的情况；无法反映两个框如何相交的。

GIOU Loss（Generalized）

进化二：不相交时，IOU=0，两个框距离变换，IOU loss不变，改进为GIOU。

GIOU Loss，在IOU的基础上引入了预测框和真实框的最小外接矩形。

GIoU公式：

 GIoU Loss公式：

GIOU算法流程如下：

当两框完全重合时取最小值0，当两框的边外切时，损失函数值为1；

当两框分离且距离很远时，损失函数值为2。

使用外接矩形的方法不仅可以反应重叠区域的面积，还可以计算非重叠区域的比例，因此GIOU损失函数能更好的反应真实框和预测框的重合程度和远近距离。

GIOU Loss存在的问题：

1）包含时计算得到的IOU、GIOU数值相等，损失函数值与IOUloss 一样，无法很好的衡量其相对的位置关系。

2）同时在计算过程中出现上述情况，预测框在水平或垂直方向优化困难，导致收敛速度慢。

DIoU Loss（Distance）

进化三：包含时，AUB不变，两个框距离变换，GIOU loss不变，改进为DIOU。

DIoU公式：

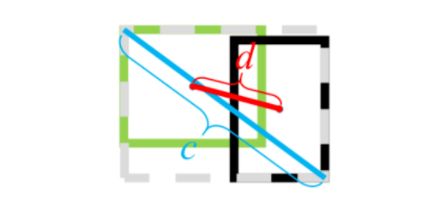
d是A框与B框中心点坐标的欧式距离，而c 则是包住它们的最小方框的对角线距离。

DIoU Loss公式：

DIoU Loss的优点：

DIoU的惩罚项是基于中心点的距离和对角线距离的比值，避免了像GIoU在两框距离较远时，产生较大的外包框，Loss值较大难以优化。

所以DIoU Loss收敛速度会比GIoU Loss快。

即使在一个框包含另一个框的情况下，c值不变，但d值也可以进行有效度量。

DIoU Loss存在的问题：

中心点重合，但宽高比不同时，DIOU loss不变。

CIOU Loss（Complete）

进化四：中心点重合，中心点距离不变，DIOU Loss不变，但宽高比不同改进为CIOU。

在两个框中心点重合时，c与d的值都不变。所以此时需要引入框的宽高比：

CIOU公式：

其中α 是权重函数，v 用来度量宽高比的一致性：

CIoU Loss公式：

GIoU：为了归一化坐标尺度，利用IoU，并初步解决IoU为零的情况。
DIoU：DIoU损失同时考虑了边界框的重叠面积和中心点距离。
然而，anchor框和目标框之间的长宽比的一致性也是极其重要的。

一个好的目标框回归损失应该考虑三个重要的几何因素：重叠面积、中心点距离、长宽比。

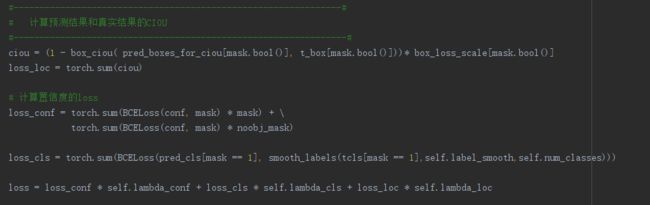
YOLO V4相较于YOLO V3，只在bounding box regression做了创新，用CIOU代替了MSE，其他两个部分没有做实质改变

EIOU Loss

CIOU Loss虽然考虑了边界框回归的重叠面积、中心点距离、纵横比。

但是通过其公式中的v反映的纵横比的差异，而不是宽高分别与其置信度的真实差异，所以有时会阻碍模型有效的优化相似性。

在CIOU的基础上将纵横比拆开，提出了EIOU Loss，并且加入Focal聚焦优质的锚框。

EIOU的惩罚项是在CIOU的惩罚项基础上将纵横比的影响因子拆开分别计算目标框和锚框的长和宽，该损失函数包含三个部分：重叠损失，中心距离损失，宽高损失，前两部分延续CIOU中的方法，但是宽高损失直接使目标盒与锚盒的宽度和高度之差最小，使得收敛速度更快。

惩罚项公式如下：

EIOU Loss优点：

1）将纵横比的损失项拆分成预测的宽高分别与最小外接框宽高的差值，加速了收敛提高了回归精度。

2）引入了Focal Loss优化了边界框回归任务中的样本不平衡问题，即减少与目标框重叠较少的大量锚框对BBox 回归的优化贡献，使回归过程专注于高质量锚框。

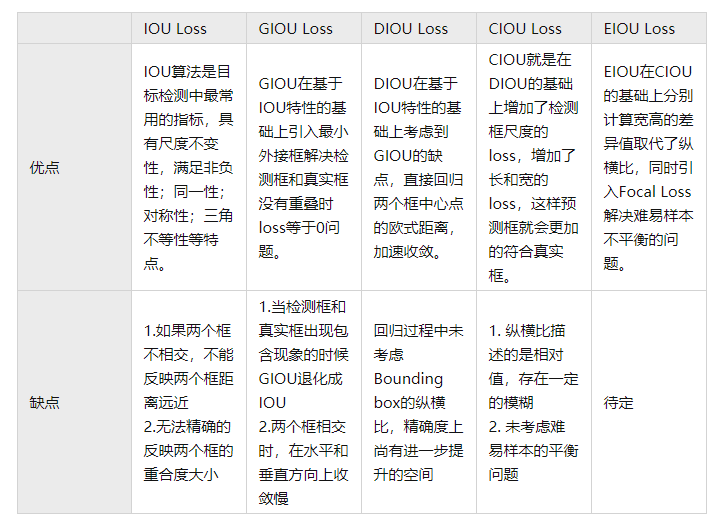
总结

   

 ——————

浅谈则止，细致入微AI大道理

扫描下方“AI大道理”，选择“关注”公众号

—————————————————————

 

  

—————————————————————

投稿吧   | 留言吧