PTA数据结构与算法-第六章——图

---

第一章——褚论

第二章——线性表

第三章——栈与队列

第四章——字符串

第五章——树与二叉树

第六章——图

第七章——排序

第八章——检索

---

判断题

1-1
无向连通图所有顶点的度之和为偶数。
T

扩展

无向连通图的特性。
Ⅰ．每条边都连接了两个结点，则在计算顶点的度之时，这条边都被计算了两次，故所有顶点的度之和为边数的两倍，显然必为偶数。
Ⅱ．边数大于等于顶点个数减1，如果定点数为3，则边数为2，边数=定点个数减1；
Ⅲ．在顶点数n≥3的完全有向图中，没有度为1的节点，并且边数与顶点数的差要大于等于0。

---

1-2
无向连通图边数一定大于顶点个数减1。
F
顶点数为3时，等于；

---

1-3
用邻接表法存储图，占用的存储空间数只与图中结点个数有关，而与边数无关。
F

---

1-4
用邻接矩阵法存储图，占用的存储空间数只与图中结点个数有关，而与边数无关。
T

---

1-5
在一个有向图中，所有顶点的入度与出度之和等于所有边之和的2倍。
T

---

1-6
在任一有向图中，所有顶点的入度之和等于所有顶点的出度之和。
T

---

1-7
如果无向图G必须进行两次广度优先搜索才能访问其所有顶点，则G一定有2个连通分量。
T

---

1-8
Prim 算法是维护一个森林，每一步把两棵树合并成一棵。
F
Prim算法是构造最小生成树的算法。

---

1-9
Kruskal 算法是维护一个森林，每一步把两棵树合并成一棵。
T

---

1-10
Kruskal 算法是通过每步添加一条边及其相连的顶点到一棵树，从而逐步生成最小生成树。
F

---

1-11
Prim 算法是通过每步添加一条边及其相连的顶点到一棵树，从而逐步生成最小生成树。
T

---

1-12
无向连通图至少有一个顶点的度为1。
F
在顶点数n≥3的完全有向图中，没有度为1的节点，并且边数与顶点数的差要大于等于0。

---

1-13
用一维数组G[]存储有4个顶点的无向图如下：
G[ ] = { 0, 1, 0, 1, 1, 0, 0, 0, 1, 0 }
则顶点2和顶点0之间是有边的。
T

---

单选题

2-1
下面关于图的存储的叙述中，哪一个是正确的？

用相邻矩阵法存储图，占用的存储空间数只与图中结点个数有关，而与边数无关
用相邻矩阵法存储图，占用的存储空间数只与图中边数有关，而与结点个数无关
用邻接表法存储图，占用的存储空间数只与图中结点个数有关，而与边数无关
用邻接表法存储图，占用的存储空间数只与图中边数有关，而与结点个数无关

---

2-2
关于图的邻接矩阵，下列哪个结论是正确的？

有向图的邻接矩阵总是不对称的
有向图的邻接矩阵可以是对称的，也可以是不对称的
无向图的邻接矩阵总是不对称的
无向图的邻接矩阵可以是不对称的，也可以是对称的

---

2-3
设N个顶点E条边的图用邻接表存储，则求每个顶点入度的时间复杂度为：

O(N)
O(N​²)
O(N+E)
O(N×E)

---

2-4
在任一有向图中，所有顶点的入度之和与所有顶点的出度之和的关系是：

相等
大于等于
小于等于
不确定

---

2-5
下面给出的有向图中，有__个强连通分量。

1 ({0,1,2,3,4})
1 ({1,2,3,4})
2 ({1,2,3,4}, {0})
5 ({0}, {1}, {2}, {3}, {4})

---

2-6
给定一个有向图的邻接表如下图，则该图有__个强连通分量。

4 {{0, 1, 5}, {2}, {3}, {4}}
3 {{2}, {4}, {0, 1, 3, 5}}
1 {0, 1, 2, 3, 4, 5}
1 {0, 5, 1, 3}

---

2-7
对于一个具有N个顶点的无向图，要连通所有顶点至少需要多少条边？
N−1
N
N+1
N/2

---

2-8
一个有N个顶点的强连通图至少有多少条边？

N−1
N
N+1
N(N−1)

---

2-9
对于有向图，其邻接矩阵表示比邻接表表示更易于：

=求一个顶点的入
求一个顶点的出边邻接点
进行图的深度优先遍历
进行图的广度优先遍历

---

2-10
在用邻接表表示有N个结点E条边的图时，深度优先遍历算法的时间复杂度为：

O(N)
O(N+E)
O(N^​2)
O(N^​2 ×E)

---

2-11
给定一有向图的邻接表如下。从顶点V1出发按深度优先搜索法进行遍历，则得到的一种顶点序列为：

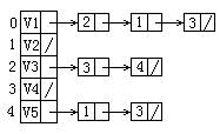
V1,V2,V3,V5,V4
V1,V3,V4,V5,V2
V1,V4,V3,V5,V2
V1,V2,V4,V5,V3

---

2-12
已知一个图的邻接矩阵如下，则从顶点V1出发按深度优先搜索法进行遍历，可能得到的一种顶点序列为：

V1,V2,V3,V4,V5,V6
V1,V2,V4,V5,V6,V3
V1,V3,V5,V2,V4,V6
V1,V3,V5,V6,V4,V2

---

2-13
如果从无向图的任一顶点出发进行一次深度优先搜索可访问所有顶点，则该图一定是：

连通图
完全图
有回路的图
一棵树

---

2-14
给定一有向图的邻接表如下。从顶点V1出发按广度优先搜索法进行遍历，则得到的一种顶点序列为：

V1,V2,V3,V4,V5
V1,V2,V3,V5,V4
V1,V3,V2,V4,V5
V1,V4,V3,V5,V2

---

2-15
已知一个图的邻接矩阵如下，则从顶点V1出发按广度优先搜索法进行遍历，可能得到的一种顶点序列为：

V1,V2,V3,V5,V4,V6
V1,V2,V4,V5,V6,V3
V1,V3,V5,V2,V4,V6
V1,V3,V5,V6,V4,V2

---

2-16
图的广度优先遍历类似于二叉树的：

先序遍历
中序遍历
后序遍历
层次遍历

---

2-17
我们用一个有向图来表示航空公司所有航班的航线。下列哪种算法最适合解决找给定两城市间最经济的飞行路线问题？

Dijkstra算法
Kruskal算法
深度优先搜索
拓扑排序算法

解析：

单源最短路径——Dijkstra算法
每对顶点最短路径——Floyd算法

---

2-18
数据结构中Dijkstra算法用来解决哪个问题？

关键路径
最短路径
拓扑排序
字符串匹配

---

2-19
使用迪杰斯特拉（Dijkstra）算法求下图中从顶点1到其他各顶点的最短路径，依次得到的各最短路径的目标顶点是：

5, 2, 3, 4, 6
5, 2, 3, 6, 4
5, 2, 4, 3, 6
5, 2, 6, 3, 4

---

2-20
任何一个带权无向连通图的最小生成树——

是唯一的
是不唯一的
有可能不唯一
有可能不存在

---

2-21
给定有权无向图的邻接矩阵如下，其最小生成树的总权重是：

10
11
12
14

2+4+1+7=14

---

2-22
对下图进行拓扑排序，可以得到不同的拓扑序列的个数是：

4
3
2
1

解析：可以得到：
aebcd abced abecd

---

2-23
使用迪杰斯特拉（Dijkstra）算法求下图中从顶点1到其他各顶点的最短路径，依次得到的各最短路径的目标顶点是：

6, 7, 5, 3, 2, 4
6, 2, 5, 7, 3, 4
2, 3, 4, 5, 6, 7
2, 4, 3, 6, 5, 7

---

程序填空题

5-1
下列代码的功能是对一个给定的图G执行拓扑排序，其中TopNum[]从1开始记录拓扑序。

void Topsort( Graph G )
{
   Queue Q;
   Vertex V, W;
   NodePtr ptr;
   int counter = 0;

   Q = CreateEmptyQueue(NumVertex);
   for ( V=0; V<G->NumV; V++ )
      if ( Indegree[V] == 0 )
         Enqueue(V, Q);
   while ( !IsEmpty(Q) ){
      V = Dequeue( Q );
      TopNum[V] = 
++counter
;
      for ( ptr=G->List[V]; ptr; ptr=ptr->Next) {
         W = ptr->Vertex;
         if ( 
--Indegree[W]
 == 0 )
            Enqueue(W, Q);
      }
   }
   if ( counter != NumVertex )
      printf("ERROR: Graph has a cycle.\n");
   DisposeQueue(Q);
}

++counter
–Indegree[W]

---

5-2

/*  广度优先遍历邻接矩阵存储的图Graph  */
typedef struct {
	Vertex G[MAX][MAX];
	int Nv;
}Graph;
typedef Graph* MGraph;
typedef struct {
	Vertex *vertex;
	int len;
	int ptr;
	int end;
}queue;
typedef queue* Queue;

/* IsEdge(Graph, V, W)检查是否图Graph中的一条边，即W是否V的邻接点。  */
bool IsEdge( MGraph Graph, Vertex V, Vertex W )
{
    return Graph->G[V][W]<INFINITY ? true : false;
}

/* Visited[]为布尔类型全局数组，已经初始化为false */
void BFS ( MGraph Graph, Vertex S, void (*Visit)(Vertex) )
{   
    Queue Q;     
    Vertex V, W;

    Q = CreateQueue( MaxSize ); 
    Visit( S );
    Visited[S] = true; 
    
AddQ(Q, S)
;

    while ( !IsEmpty(Q) ) {
        
V = DeleteQ(Q)
;  
        for( W=0; W<Graph->Nv; W++ ) 
            if ( 
!Visited[W] && IsEdge(Graph, V, W)
 ) { 
                Visit( W );
                Visited[W] = true; 
                AddQ(Q, W); 
            }
    } /* while结束*/
}

V = DeleteQ(Q)
!Visited[W] && IsEdge(Graph, V, W)