Seaborn数据可视化的学习(自用笔记)
文章目录
- 前言
- 一、缺失值与异常值处理
-
- 1、删除缺失值
-
- dropna()函数
- 2、处理数值型数据的异常值
-
- boxplot()或者catplot()
- 二、"kde"密度曲线与直方图结合
-
- 1、单独画直方图
- 2、单独画"kde"曲线
- 3、直方图与kde曲线结合
- 三、kde曲线用来比较测试集与训练集的分布
- 四、数值变量关系的各类曲线
-
- 1、(经验累积)分布函数ecdf曲线
- 2、两变量之间的关系---散点图relplot()
- 3、两变量之间的关系--连线图lineplot
- 4、回归拟合,两个数值型变量之间的线性关系 implot()
- 5、绘制两个变量的联合分布
-
- 联合分布之kde曲线
- 联合分布之直方图
- 6、jointplot()同时绘制两个变量的联合分布和各自分布
-
- 联合分布用回归拟合,各自分布用直方图叠加'kde'曲线
- 联合分布用散点图,各自分布用直方图
- 在不同类别下画出两变量的联合分布及其各自分布
- 进阶:自定义联合分布和各自分布所要画的图
- 7、成对的绘制所有数值变量之间的联合分布
- 8、data.corr()+sns.heatmap():成对绘制所有数值变量的相关系数矩阵图---即热力图
- 五、类别变量的分布
-
- 1、类别变量的计数
- 2、类别变量与数值变量的关系barplot()/pointplot
- 3、不同类别中数值变量的取值范围 :boxplot/boxenplot
- 4、不同类别中数值变量的分布图
-
- 带状图 :带状图是散点图和直方图的结合
- 小提琴图
- 带状图覆盖在小提琴图上
- 六、FaceGride()、PairGrid自定义绘制函数
- 至此本篇笔记结束
前言
一、缺失值与异常值处理
当我们刚拿到数据的时候,必须先处理数据中的缺失值与异常值 一般来说 缺失值可以直接删除 也可批量填充以平均值 这边就不详细介绍fill填充了
1、删除缺失值
dropna()函数
DataFrame.dropna(axis=0,how='any',subset=None,inplace=False)
- how='any’时表示删除只要含有缺失值的行(列)
- axis=0 表示删除行 axis=1表示删除列
- subset可以自由选择要在哪些列中寻找缺失值
- inplace表示直接在原DataFrame修改
df.dropna(subset=['name', 'born']) #删除在'name' 'born'列含有缺失值的行
2、处理数值型数据的异常值
排除数据分布偏移严重的情况,一般情况下我们会画出箱型图来处理异常值
boxplot()或者catplot()
sns.boxplot(data=df,x='评分')
sns.catplot(data=df,x='评分',kind='box')
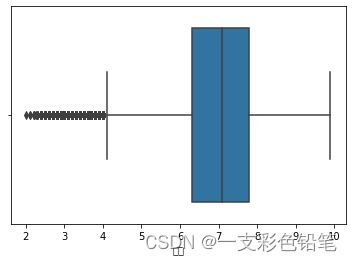
操作后可以发现两张图几乎一模一样(这边只给出一张)
箱体外的两条线是表示合理范围内的最大值和最小值(用公式计算出来的),超出这个范围的话,数据就是不合理的,有可能是异常值,需要具体情况具体分析。
那么这边我们就只取≥4.1 且 ≤9.8的数据
dff=df[(df['评分']>=4.1)&(df['评分']<=9.8)]
二、"kde"密度曲线与直方图结合
1、单独画直方图
sns.displot(data=df,x='评分',kind='hist') # 参数bins 来设置区间个数
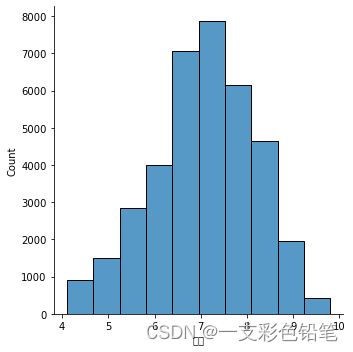
设置各种大小的bins值后我们发现 bins划分过粗可能会忽略数据的分布特征,但有时划分过细又会导致过分解读。 下图是bins为40时的图
还有参数shrink 如果直方图的柱子过于粗矮,可以通过该参数来放缩拉长
sns.displot(data=df,x='评分',kind='hist',bins=40) # 参数bins 来设置区间个数
2、单独画"kde"曲线
sns.displot(data=df,x='评分',kind='kde')
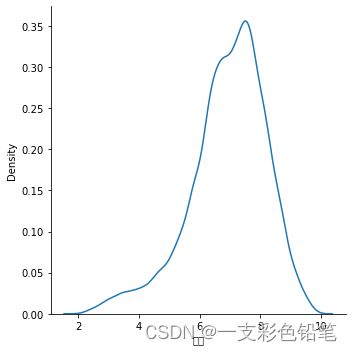
图画得不错 但是深入研究发现

该数据的最大值和最小值分别是9.9和2.0 而图所示画的数据下标超过了这个范围
为了优化这个细节,同时让分布更便于观察
我们可以先画一个直方图,再在直方图上面叠加一个kde曲线
3、直方图与kde曲线结合
sns.displot(data=df,x='评分',kind='hist',kde=True) #kde=True实现了这个需求
三、kde曲线用来比较测试集与训练集的分布
注:kde曲线可以用来比较训练集和测试集变量分布大体是否一致 从来判断划分得是否合理
比如2022数学建模国赛C题 该题有众多影响预测结果的自变量,为了查看训练集与测试集的划分是否合理,我们不妨取其重要性评分最大的一项来画kde曲线
在上述题中 重要性评分最大的是氧化铅
import pandas as pd
import numpy as np
import matplotlib.pylab as plt
import matplotlib as mpl
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score
df=pd.read_excel(r'C:\Users\王金鹏\Desktop\决策树与随机森林.xlsx')
x=df.iloc[:,1:15]
y=df.iloc[:,-1]
#划分其中 75%为训练集,其余 25%为测试集
x_train, x_test, y_train, y_test= train_test_split(x,y,train_size=0.75)
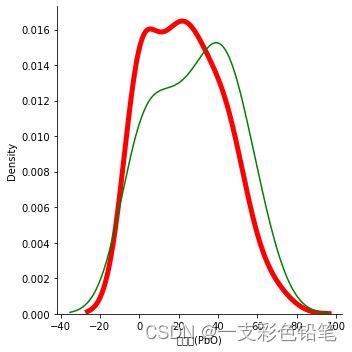
sns.displot(data=x_train,x='氧化铅(PbO)',kind='kde',linewidth=5.0,color='r')
sns.kdeplot(data=x_test,x='氧化铅(PbO)',color='g') #这边记得用kdeplot 才能在一张图上
四、数值变量关系的各类曲线
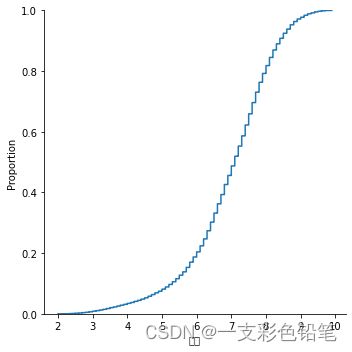
1、(经验累积)分布函数ecdf曲线
sns.displot(data=df,x='评分',kind='ecdf')
2、两变量之间的关系—散点图relplot()
dff=dff[(dff['年代']<2022)&(dff['年代']>1980)]
sns.relplot(data=dff,x='年代',y='评分')
下图是1980年到2022年时期 年代与评分大小的散点图
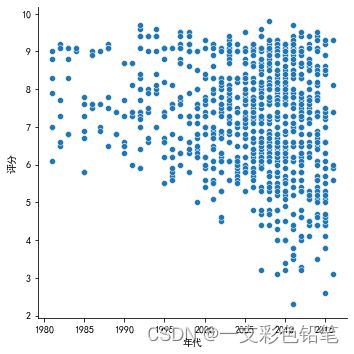
如果再加个参数hue 使得不同颜色代表不同产地的话
sns.relplot(data=dff,x='年代',y='评分',hue='产地')

还可以加参数 markers=["o","^"] 比如这个就分别用圆形和三角形来画图
因为这边没有合适的数据给大家画图,产地太多了,就不赘述了
特别的,如果分类的标准不是产地这种类别变量,如果是数值型变量,可以加参数size=‘大小’ 效果如下图,数字越大 形状越大

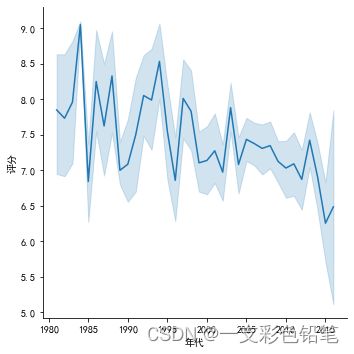
3、两变量之间的关系–连线图lineplot
连线图适合用来分析类似股价波动的情况
sns.relplot(data=dff,x='年代',y='评分',kind='line')
4、回归拟合,两个数值型变量之间的线性关系 implot()
例子来自于2022数学建模国赛C题
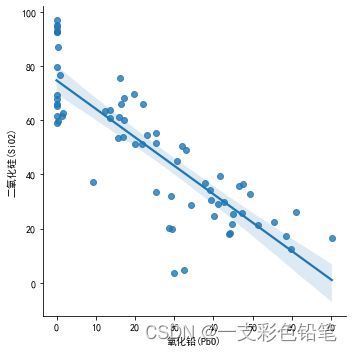
sns.lmplot(data=df,x='氧化铅(PbO)',y='二氧化硅(SiO2)')
sns.residplot(data=df,x='氧化铅(PbO)',y='二氧化硅(SiO2)',color='r')
红点为拟合后的残差 如果拟合得好的话 残差应该是随机分布而不是发散地分布 观察可得
上图拟合的效果应该较好(本人也不太懂,说错可以告诉我)
而如果残差分布比较分散的时候,拟合效果不好时 说明变量之间的关系我们还未充分挖掘
5、绘制两个变量的联合分布
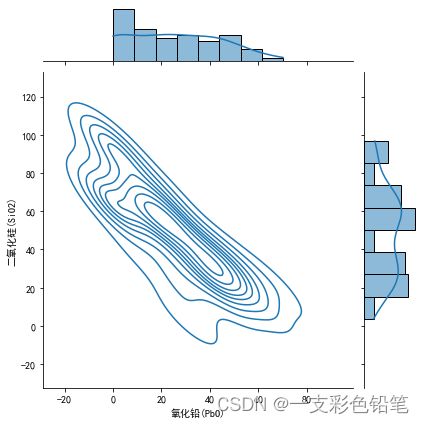
联合分布之kde曲线
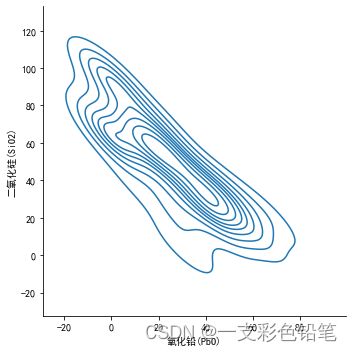
sns.displot(data=df,x='氧化铅(PbO)',y='二氧化硅(SiO2)',kind='kde')
- 可以利用参数thresh 控制显示的范围
thresh 取值区间为[0,1]
thresh=0.2时
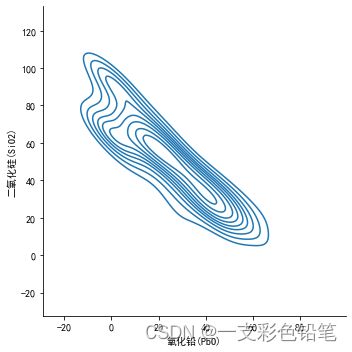
thresh=0.5时
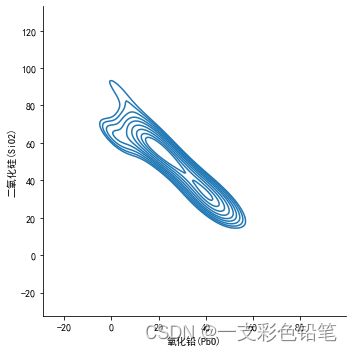
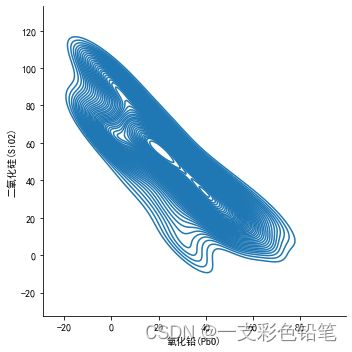
最后 参数levels 来指定你要画多少条线,越大越密,越小越稀疏,这边稍微展示一下
sns.displot(data=df,x='氧化铅(PbO)',y='二氧化硅(SiO2)',kind='kde',levels=50)
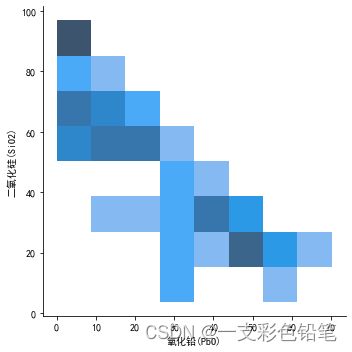
联合分布之直方图
sns.displot(data=df,x='氧化铅(PbO)',y='二氧化硅(SiO2)',kind='hist')
6、jointplot()同时绘制两个变量的联合分布和各自分布
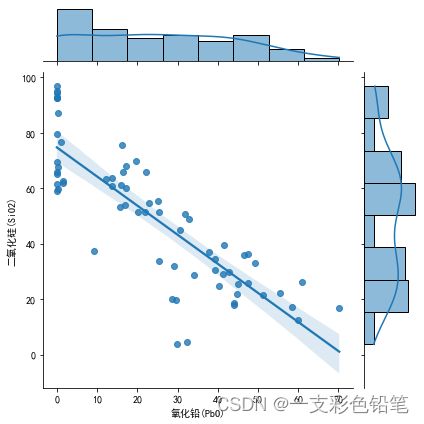
联合分布用回归拟合,各自分布用直方图叠加’kde’曲线
sns.jointplot(data=df,x='氧化铅(PbO)',y='二氧化硅(SiO2)',kind='reg')
联合分布用散点图,各自分布用直方图
sns.jointplot(data=df,x='氧化铅(PbO)',y='二氧化硅(SiO2)')
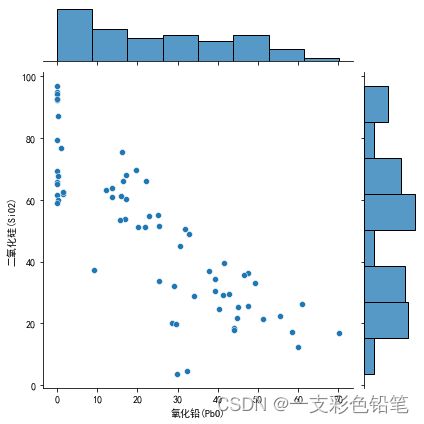
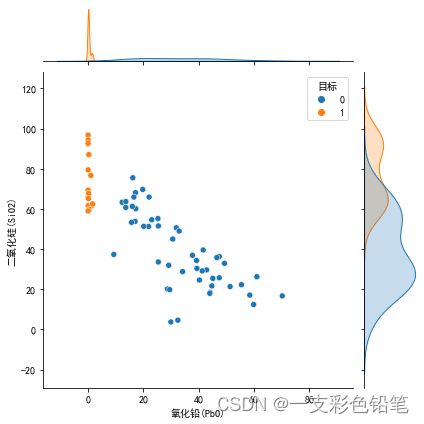
例子来自2022数模国赛C题 0和1分别高钾和铅钡两种类别的玻璃
在不同类别下画出两变量的联合分布及其各自分布
实现该操作只需要多加一个参数hue
sns.jointplot(data=df,x='氧化铅(PbO)',y='二氧化硅(SiO2)',hue='目标')
进阶:自定义联合分布和各自分布所要画的图
例如,联合分布想画kde曲线,各自分布想画箱型图 可利用JointGrid()实现
g=sns.JointGrid(data=df,x='氧化铅(PbO)',y='二氧化硅(SiO2)')
g.plot(sns.kdeplot,sns.boxplot) #自定义类型
g=sns.JointGrid(data=df,x='氧化铅(PbO)',y='二氧化硅(SiO2)')
g.plot_joint(sns.kdeplot)
g.plot_marginals(sns.histplot,kde=True)
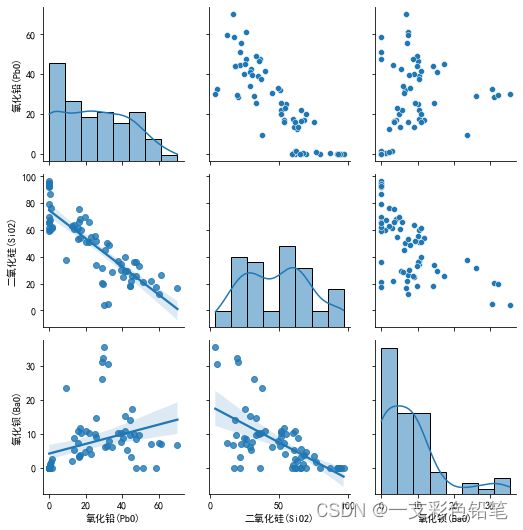
7、成对的绘制所有数值变量之间的联合分布
sns.pairplot(data=df.iloc[:,0:5])
下图对角线上的图就是各自变量的直方图 其余散点图为联合分布的散点图

最后,这种成对绘制也可以自定义联合分布和各自分布所需的图像
比如,我们对角线想绘制直方图叠加kde 上三角绘制散点图 下三角绘制回归拟合
g=sns.PairGrid(data=df,x_vars=['氧化铅(PbO)','二氧化硅(SiO2)','氧化钡(BaO)'],y_vars=['氧化铅(PbO)','二氧化硅(SiO2)','氧化钡(BaO)'])
g.map_upper(sns.scatterplot)
g.map_diag(sns.histplot,kde=True)
g.map_lower(sns.regplot)
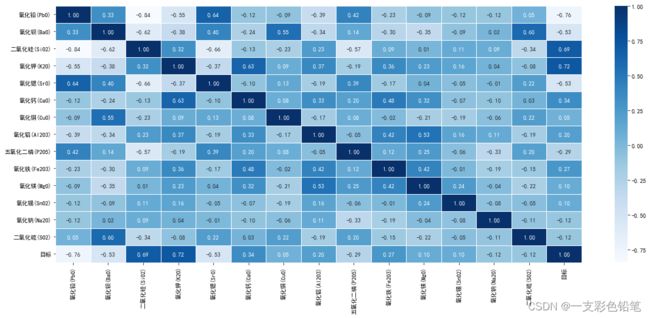
8、data.corr()+sns.heatmap():成对绘制所有数值变量的相关系数矩阵图—即热力图
var_cor=df.corr()
plt.figure(figsize=(20,8))
sns.heatmap(var_cor,linewidths=0.5,annot=True,fmt='.2f',cmap='Blues')
#cmap设置颜色
#annot=True 表示显示数字
#fmt='.2f'表示保存小数点后两位
#linewidth控制格子间的间隙
//共有数百种颜色格式:'Accent', 'Accent_r', 'Blues', 'Blues_r', 'BrBG', 'BrBG_r', 'BuGn', 'BuGn_r', 'BuPu', 'BuPu_r', 'CMRmap', 'CMRmap_r', 'Dark2', 'Dark2_r', 'GnBu', 'GnBu_r', 'Greens', 'Greens_r', 'Greys', 'Greys_r', 'OrRd', 'OrRd_r', 'Oranges', 'Oranges_r', 'PRGn', 'PRGn_r', 'Paired', 'Paired_r', 'Pastel1', 'Pastel1_r', 'Pastel2', 'Pastel2_r', 'PiYG', 'PiYG_r', 'PuBu', 'PuBuGn', 'PuBuGn_r', 'PuBu_r', 'PuOr', 'PuOr_r', 'PuRd', 'PuRd_r', 'Purples', 'Purples_r', 'RdBu', 'RdBu_r', 'RdGy', 'RdGy_r', 'RdPu', 'RdPu_r', 'RdYlBu', 'RdYlBu_r', 'RdYlGn', 'RdYlGn_r', 'Reds', 'Reds_r', 'Set1', 'Set1_r', 'Set2', 'Set2_r', 'Set3', 'Set3_r', 'Spectral', 'Spectral_r', 'Wistia', 'Wistia_r', 'YlGn', 'YlGnBu', 'YlGnBu_r', 'YlGn_r', 'YlOrBr', 'YlOrBr_r', 'YlOrRd', 'YlOrRd_r', 'afmhot', 'afmhot_r', 'autumn', 'autumn_r', 'binary', 'binary_r', 'bone', 'bone_r', 'brg', 'brg_r', 'bwr', 'bwr_r', 'cividis', 'cividis_r', 'cool', 'cool_r', 'coolwarm', 'coolwarm_r', 'copper', 'copper_r', 'crest', 'crest_r', 'cubehelix', 'cubehelix_r', 'flag', 'flag_r', 'flare', 'flare_r', 'gist_earth', 'gist_earth_r', 'gist_gray', 'gist_gray_r', 'gist_heat', 'gist_heat_r', 'gist_ncar', 'gist_ncar_r', 'gist_rainbow', 'gist_rainbow_r', 'gist_stern', 'gist_stern_r', 'gist_yarg', 'gist_yarg_r', 'gnuplot', 'gnuplot2', 'gnuplot2_r', 'gnuplot_r', 'gray', 'gray_r', 'hot', 'hot_r', 'hsv', 'hsv_r', 'icefire', 'icefire_r', 'inferno', 'inferno_r', 'jet', 'jet_r', 'magma', 'magma_r', 'mako', 'mako_r', 'nipy_spectral', 'nipy_spectral_r', 'ocean', 'ocean_r', 'pink', 'pink_r', 'plasma', 'plasma_r', 'prism', 'prism_r', 'rainbow', 'rainbow_r', 'rocket', 'rocket_r', 'seismic', 'seismic_r', 'spring', 'spring_r', 'summer', 'summer_r', 'tab10', 'tab10_r', 'tab20', 'tab20_r', 'tab20b', 'tab20b_r', 'tab20c', 'tab20c_r', 'terrain', 'terrain_r', 'turbo', 'turbo_r', 'twilight', 'twilight_r', 'twilight_shifted', 'twilight_shifted_r', 'viridis', 'viridis_r', 'vlag', 'vlag_r', 'winter', 'winter_r'
五、类别变量的分布
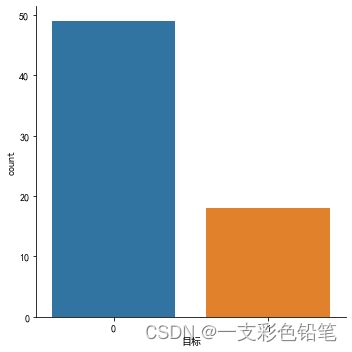
1、类别变量的计数
sns.catplot(data=df,x='目标',kind='count')
2、类别变量与数值变量的关系barplot()/pointplot
下图是绘制不同类别中数值变量的均值/中值估计 :
sns.catplot(data=df,x='目标',y='二氧化硅(SiO2)',kind='bar')
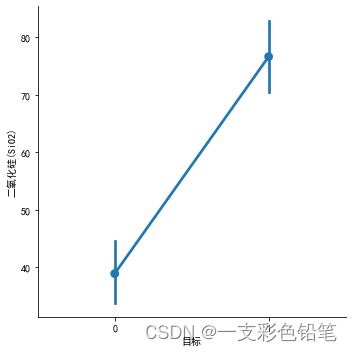
下图0表示高钾类 1表示铅钡类

如果有多个柱状图,为了画出这些图之间的变化关系,显然把柱状图上的黑线连起来就明显了
sns.catplot(data=df,x='目标',y='二氧化硅(SiO2)',kind='point')
3、不同类别中数值变量的取值范围 :boxplot/boxenplot
sns.catplot(data=df,x='目标',y='二氧化硅(SiO2)',kind='box')

一般情况下boxplot就够用了,当变量取值范围很大时,可以用boxenplot(适合大数据集)。boxenplot可以逐级地绘制箱型图。
如果大数据集中适用boxplot
可能会出现下图这种异常值划分非常多,即异常值计算不合理的情况出现
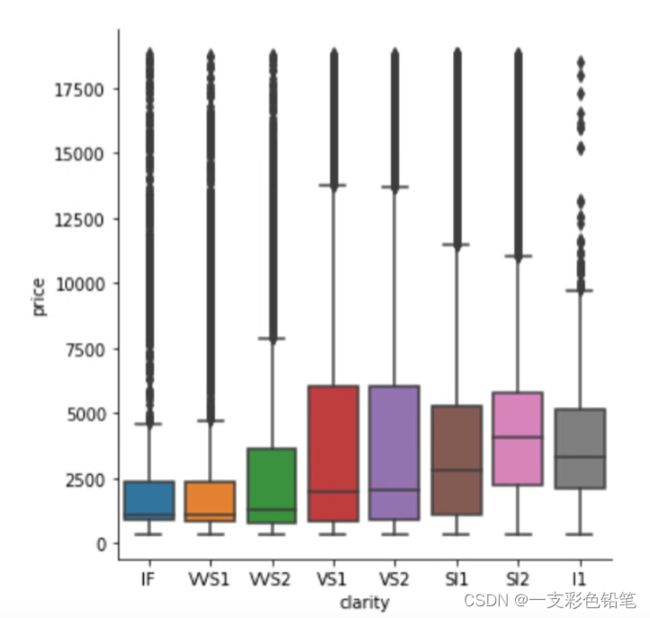
而如果适用boxenplot
则划分会变得合理 即boxenplot适合用于大数据集

4、不同类别中数值变量的分布图
带状图 :带状图是散点图和直方图的结合
sns.catplot(data=df,x='目标',y='二氧化硅(SiO2)',kind='strip')
- 通过参数
jitter可以设置带状图的宽度,取值范围[0,1]
小提琴图
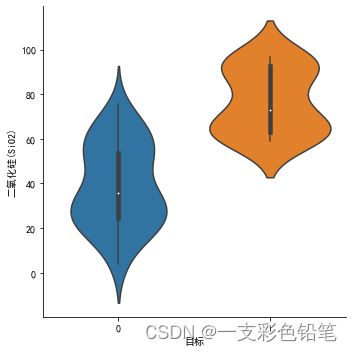
sns.catplot(data=df,x='目标',y='二氧化硅(SiO2)',kind='violin')
带状图覆盖在小提琴图上
sns.catplot(data=df,x='目标',y='二氧化硅(SiO2)',kind='violin')
sns.swarmplot(data=df,x='目标',y='二氧化硅(SiO2)',color='w',size=3)
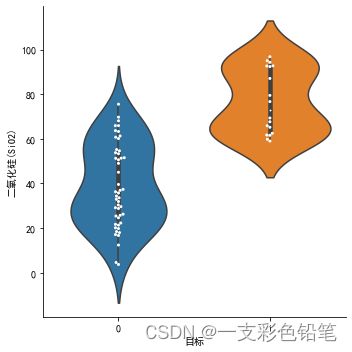
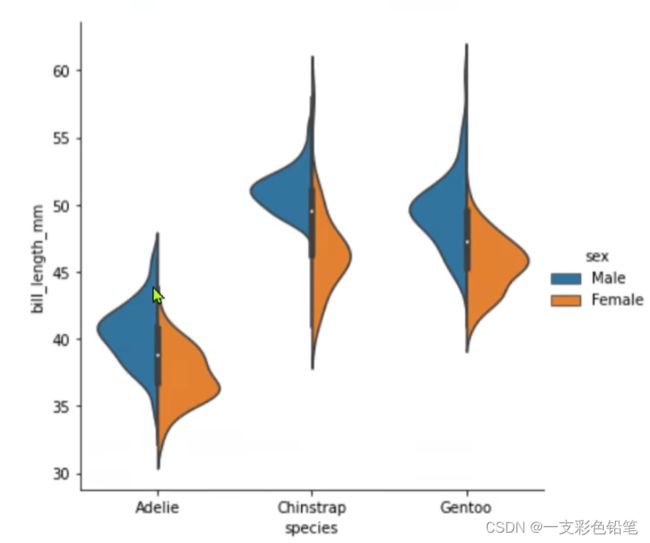
还可以再加再加一个参数hue 来观察不同类别下的情况
特别地当参数split=True时 不同类别的小提琴图会合并在一起,节省空间
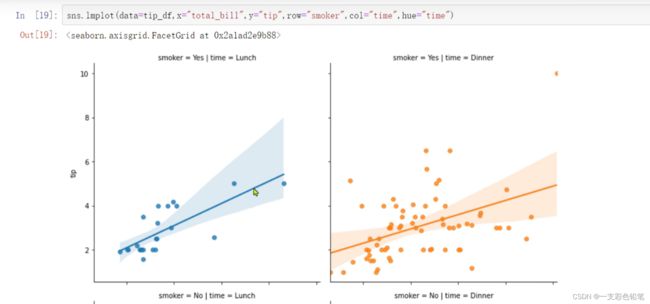
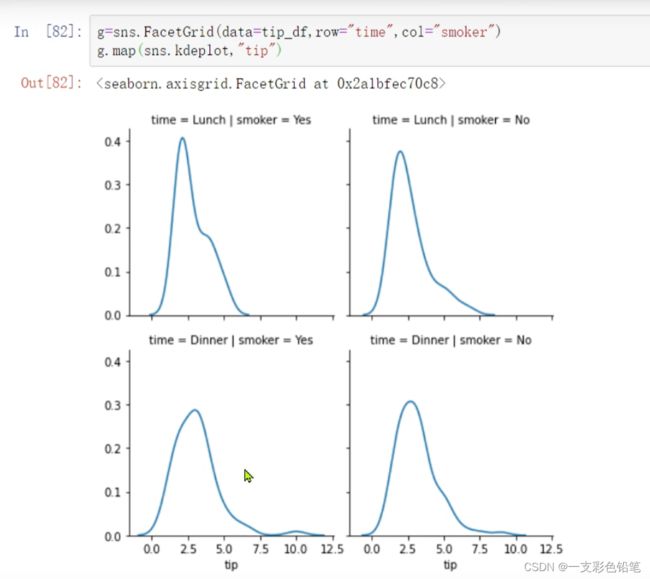
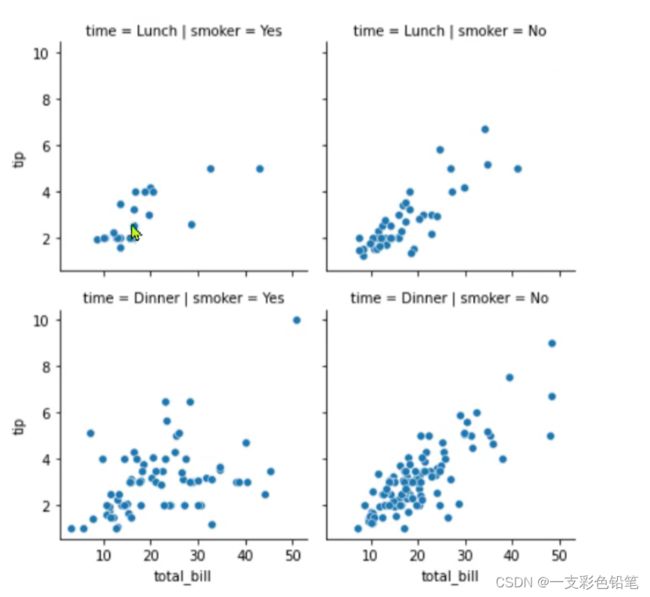
六、FaceGride()、PairGrid自定义绘制函数
这边就不多赘叙了 直接上图