使用GDAL进行坐标转换

1、地理坐标系与投影坐标系

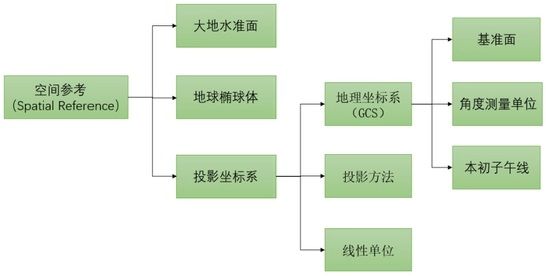
空间参考中主要包含大地水准面、地球椭球体、投影坐标系等几部分内容。地图投影就是把地球表面的任意点，利用一定数学法则，转换到地图平面上的理论和方法，一般有两种坐标系来进行表示，分别是地理坐标系和投影坐标系。如下图所示，描述了地理坐标系与投影坐标系之间的关系。

图1 地理坐标与投影坐标关系

地理坐标系即球体坐标，投影坐标即投影后的平面坐标；常见的地理坐标GPS坐标，常见的投影坐标墨卡托投影。

常用的坐标系为地理坐标系（Geograpic Coordinate System,简称GCS）和投影坐标系（Projected Coordinate System，简称PCS）。

1.1、地理坐标系统

地理坐标系统（GCS）用一个三维的球面来确定地物在地球上的位置，地面点的地理坐标有经度、纬度、高程构成。地理坐标系统与选择的地球椭球体和大地基准面有关。椭球体定义了地球的形状，而大地基准面确定了椭球体的中心。

　　地理坐标系 (GCS) 使用三维球面来定义地球上的位置。GCS中的重要参数包括角度测量单位、本初子午线和基准面（基于旋转椭球体）。地理坐标系统中用经纬度来确定球面上的点位，经度和纬度是从地心到地球表面上某点的测量角。球面系统中的水平线是等纬度线或纬线，垂直线是等经度线或经线。这些线包络着地球，构成了一个称为经纬网的格网化网络。

GCS中经度和纬度值以十进制度为单位或以度、分和秒 (DMS) 为单位进行测量。纬度值相对于赤道进行测量，其范围是 -90°（南极点）到 +90°（北极点）。经度值相对于本初子午线进行测量。其范围是 -180°（向西行进时）到 180°（向东行进时）。

1.2、投影坐标系统

投影坐标系统是根据某种映射关系，将地理坐标系统中由经纬度确定的三维球面坐标投影到二维的平面上所使用的坐标系统。在该坐标系统中，点的位置是由(x,y,z)坐标来确定的。由于投影坐标是将球面展会在平面上，因此不可避免会产生变形。这些变形包括3种：长度变形、角度变形以及面积变形。通常情况下投影转换都是在保证某种特性不变的情况下牺牲其他属性。根据变形的性质可分为等角投影、等面积投影等。

我国的基本比例尺地形图（1：5千，1：1万，1：2.5万，1：10万，1：25万，1：50万，1：100万）中，大于或等于1：50万均采用高斯-克吕格投影（Gauss_Kruger），又叫横轴墨卡托投影（Transverse Mercator）；1：100万的地形图采用正轴等角圆锥投影，又叫兰勃特投影（Lambert Conformal Conic）；海上小于50万的地形图多用正轴等角圆柱投影，又叫墨卡托投影（Mercator）。在开发GIS系统中应该采用与我国基本比例尺地形图系列一致的地图投影系统。

2、坐标系转换

根据参考文章，封装成一个类使用。

import numpy as np
from osgeo import gdal, osr

class GdalTif(object):
    def __init__(self, tif_path):
        self.tif_path = tif_path
        self.dataset = self._read_tif(tif_path)

    @staticmethod
    def _read_tif(tif_path):
        """ 读取GDAL地理数据
        :param tif_path: tif图像路径
        :return: GDAL地理数据
        """

        dataset = gdal.Open(tif_path)
        if dataset is None:
            print(tif_path + " 文件无法打开")
        return dataset

    def get_geo_trans(self):
        """ 获取仿射矩阵信息
        :return: 仿射矩阵信息有六个参数，描述的是栅格行列号和地理坐标之间的关系:
            (
                0：左上角横坐标（投影坐标，经度）；
                1：像元宽度,影像东西/水平方向分辨率；
                2：行旋转，如果图像北方朝上，该值为0；
                3：左上角纵坐标（投影坐标，纬度）；
                4：列旋转，如果图像北方朝上，该值为0；
                5：像元高度,影像南北/垂直方向分辨率；
            )
            如果图像不含地理坐标信息，默认返回值是：(0,1,0,0,0,1)
        """

        return self.dataset.GetGeoTransform()

    def get_projection(self):
        """ 获取数据投影信息
        :return: INFO
        """

        return self.dataset.GetProjection()

    def get_srs_pair(self):
        """ 获得给定数据的投影参考系和地理参考系
        :param dataset: GDAL地理数据
        :return: 投影参考系和地理参考系
        """

        prosrs = osr.SpatialReference()
        prosrs.ImportFromWkt(self.dataset.GetProjection())
        geosrs = prosrs.CloneGeogCS()
        return prosrs, geosrs

    def imagexy2geo(self, row, col):
        """ 根据GDAL的六参数模型将影像图上坐标（行列号）转为投影坐标或地理坐标（根据具体数据的坐标系统转换）
        :param dataset: GDAL地理数据
        :param row: 像素的行号(i)
        :param col: 像素的列号(j)
        :return: 行列号(row, col)对应的投影坐标或地理坐标(x, y) - WGS84
        """

        trans = self.dataset.GetGeoTransform()
        x = trans[0] + col * trans[1] + row * trans[2]
        y = trans[3] + col * trans[4] + row * trans[5]
        return (x, y)

    def geo2imagexy(self, x, y):
        """ 根据GDAL的六 参数模型将给定的投影或地理坐标转为影像图上坐标（行列号）
        :param x: 投影或地理坐标x
        :param y: 投影或地理坐标y
        :return: 影坐标或地理坐标(x, y)对应的影像图上行列号(row, col)
        """

        trans = self.dataset.GetGeoTransform()
        a = np.array([[trans[1], trans[2]], [trans[4], trans[5]]])
        b = np.array([x - trans[0], y - trans[3]])
        return np.linalg.solve(a, b)[::-1]  # 使用numpy的linalg.solve进行二元一次方程的求解

    def geo_to_lonlat(self, x, y):
        """ 将投影坐标转为经纬度坐标（具体的投影坐标系由给定数据确定）
        :param x: 投影坐标x
        :param y: 投影坐标y
        :return: 投影坐标(x, y)对应的经纬度坐标(lon, lat)
        """

        prosrs, geosrs = self.get_srs_pair()
        ct = osr.CoordinateTransformation(prosrs, geosrs)
        coords = ct.TransformPoint(x, y)
        return coords[:2]

    def lonlat2geo(self, lon, lat):
        """ 将经纬度坐标转为投影坐标（具体的投影坐标系由给定数据确定）
        :param dataset: GDAL地理数据
        :param lon: 地理坐标lon经度
        :param lat: 地理坐标lat纬度
        :return: 经纬度坐标(lon, lat)对应的投影坐标
        """

        prosrs, geosrs = self.get_srs_pair()
        ct = osr.CoordinateTransformation(geosrs, prosrs)
        coords = ct.TransformPoint(lon, lat)
        return coords[:2]

def main():
    tif_file = r"C:\Users\i\Desktop\dsm.tif"
    gda = GdalTif(tif_file)
    print("数据投影信息:", gda.get_projection())
    
    pt = (300, 500)
    print("pt = ", pt)

    print("图上坐标 -> 投影坐标：")
    point = gda.imagexy2geo(*pt)
    print("WGS84 point:", point)

    print("投影坐标 -> 图上坐标：")
    pt = gda.geo2imagexy(*point)
    print("pixel pt:", pt)

    print("投影坐标 -> 经纬度：")
    coord = gda.geo_to_lonlat(*point)
    print("gps coord:", coord)

    print("经纬度 -> 投影坐标：")
    point = gda.lonlat2geo(*coord)
    print("point:", point)

if __name__ == '__main__':
    main()

测试结果：

数据投影信息: PROJCS["CGCS2000 / 3-degree Gauss-Kruger CM 111E",GEOGCS["China Geodetic Coordinate System 2000",DATUM["China_2000",SPHEROID[
"CGCS2000",6378137,298.257222101,AUTHORITY["EPSG","1024"]],AUTHORITY["EPSG","1043"]],PRIMEM["Greenwich",0,AUTHORITY["EPSG","8901"]],UNIT["d
egree",0.0174532925199433,AUTHORITY["EPSG","9122"]],AUTHORITY["EPSG","4490"]],PROJECTION["Transverse_Mercator"],PARAMETER["latitude_of_orig
in",0],PARAMETER["central_meridian",111],PARAMETER["scale_factor",1],PARAMETER["false_easting",500000],PARAMETER["false_northing",0],UNIT["
metre",1,AUTHORITY["EPSG","9001"]],AXIS["Northing",NORTH],AXIS["Easting",EAST],AUTHORITY["EPSG","4546"]]
pt =  (300, 500)
图上坐标 -> 投影坐标：
WGS84 point: (402657.7898284429, 2052764.045716705)
投影坐标 -> 图上坐标：
pixel pt: [300. 500.]
投影坐标 -> 经纬度：
gps coord: (3.535317397929979, 124.8387146988415)
经纬度 -> 投影坐标：
point: (402657.78982844297, 2052764.0457167062)

参考文章：

1、谈谈地理坐标和投影坐标

http://www.360doc.com/content/22/1214/01/65719465_1060178233.shtml