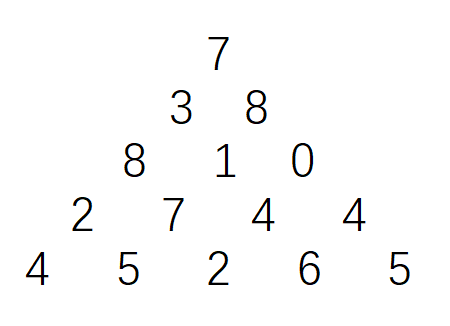算法笔记方法论3 递推法与递归法
你站在桥上看风景看风景的人在楼上看你明月装饰了你的窗子你装饰了别人的梦——卞之琳
递推算法的特点
一个问题的求解需要大量重复计算,在已知的条件和所求问题之间总存在着某种相互联系的关系,在计算时,我们需要找到这种关系,进行计算(递推关系式)。
即递推法的关键,就是找到递推关系式,这种处理方式能够将复杂的计算过程,转化为若干步骤的简单重复运送,充分利用计算机运行程序时的时间局部性和空间局部性。
递推算法的思想:
- 首要问题是先找到各个相邻数据项之间的递推关系;
- 递推关系避开了求通项公式的麻烦,且有些题目的通项公式很难求,或者不能进行求解;
- 将复杂问题分解为若干步骤的简单运算;
- 一般来说递推算法就是一种特殊的迭代算法。
递推算法解题的基本思路:
- 将复杂计算转换为简单重复运算;
- 通过找到递推关系式进行简化运算;
- 利用计算机的特性,减少运行时间。
递推算法的一般步骤:
- 根据题目确定数据项,并找到符合要求的递推关系式;
- 根据递推关系式设计递推程序;
- 根据题目找到递推的终点;
- 单次查询可以不进行存储,多次查询都要进行存储;
- 按要求输出答案即可。
递归算法:
递归算法是一种从自顶向下的算法,实际上是通过不停的直接调用或者间接的调用自身的函数,通过每次改变变量完成多个过程的重复计算,直到到达边界之后,结束调用。
与递推法相似的是,递归与递推都是将一个复杂过程分解为几个简单重复步骤进行计算。
递归算法的实现的核心是分治策略,即分而治之,将复杂过程分解为规模较小的同类问题,通过解决若干个小问题,进而解决整个复杂问题。
递归算法的思想:
- 将复杂计算过程转换为简单重复子过程;
- 找到递归公式,即能够将大问题转化为小问题的公式;
- 自上而下计算,在返回完成递归过程。
递归算法设计的一般步骤:
- 根据题目设计递归函数中的运算部分;
- 根据题目找到递归公式,题目可能会隐含给出,也可能需要自己进行推导;
- 找到递归出口,即递归的终止条件。
递归法的和递推法的思路也给大家讲的差不多了,我们结合真实大赛题目给大家进行讲解。
题目08 斐波那契数列
在一定情况下,同一个问题可以使用用递归也可以使用递推解答。一般一个问题的递推关系和递归关系都好求的话就都可以解题。
当然如果题目只有一个关系好求,那就最好采用关系好求的办法。
题目描述:
斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”。
指的是这样一个数列:0、1、1、2、3、5、8、13、21、34、……
在数学上,斐波那契数列以如下被以递推的方法定义:F(0)=0,F(1)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 2,n ∈ N*)
请求出该数列中第n个数字(n从1开始计数)是多少。
样例:
输入样例
样例1输入
6
样例2输入
4
输出样例
样例1输出
8
样例2输出
3
对于上面的样例我们进行了如下计算;
[0]=0
[1]=1
[2]=0+1
[3]=1+1=2
[4]=1+2=3
[5]=2+3=5
[6]=5+3=8
运行限制:
1. 最大运行时间:1s
2. 最大运行内存:128M
递归算法的通用框架如下:
do(a,b,c...)
{
//递归终止条件,即出口
if(a==? ,b==? ,....) return
//递归条件
if(条件1)
do(参数1)
else(条件2)
do(参数2)
}
如本题,各子式间存在计算关系,可以化为:
do(a)
{
if(a==0) return 0;
if(a==1) return 1;
return do(a-1)+do(a-2);
}
代码:
import java.util.Scanner;
public class _08斐波那契数列 {
public static void main(String[] args) {
}
// 递推
static void f1() {
int n; //第几个数
int x=0; //F(n)
int y=1; //F(n+1)
int ans = 0; //F(n+2)
Scanner in = new Scanner(System.in);
n = in.nextInt();
if(n==0) ans=0;
else if(n==1) ans=1;
else {
for(int i=2;i<=n;i++)
{
ans=x+y;
x=y;
y=ans;
}
}
System.out.println(ans);
}
// 递归
static void f2() {
int n; //第几个数
int ans = 0;
Scanner in = new Scanner(System.in);
n = in.nextInt();
ans=fn(n);
System.out.println(ans);
}
static int fn(int n)
{
if(n==0)
return 0;
//递归出口2
else if(n==1 )
return 1;
else
return fn(n-1)+fn(n-2); //递归关系式
}
}
存储版递归和递推:
public class Main {
static int []F=new int [35];
static void init() {
F[0]=0;
F[1]=1;
for(int i=2;i<=30;i++) {
F[i]=F[i-1]+F[i-2];
}
}
public static void main(String[] args) {
int m; //m次查询
int n; //第几个数
init();
Scanner in = new Scanner(System.in);
m = in.nextInt();
while(m>0){
m-=1;
n= in.nextInt();
System.out.println(F[n]);
}
}
}
public class Main {
static int []F=new int [35];
static int fn(int n)
{
//递归出口1
if(n==0) {
F[0]=0;
return 0;
}
//递归出口2
else if(n==1 ) {
F[1]=1;
return 1;
} else {
F[n]=fn(n-1)+fn(n-2);
return F[n]; //递归关系式
}
}
public static void main(String[] args) {
int m; //m次查询
int n; //第几个数
fn(30);
Scanner in = new Scanner(System.in);
m = in.nextInt();
while(m>0){
m-=1;
n= in.nextInt();
System.out.println(F[n]);
}
}
}
题目09 数字三角形
题目描述:
如图数字三角形。如下所示为一个数字三角形。请编一个程序计算从顶到底的某处的一条路径,使该路径所经过的数字总和最大。只要求输出总和。
1. 一步可沿左斜线向下或右斜线向下走;
2. 三角形行数小于等于 100;
3. 三角形中的数字为 0,1,…,99;
测试数据通过键盘逐行输入。
如上例数据应以样例所示格式输入:
样例:
输入:
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
输出:
30
运行限制:
1. 最大运行时间:1s
2. 最大运行内存:128M
代码:
import java.util.Scanner;
public class _09数字三角形 {
static int [][]a=new int [101][101];
public static void main(String[] args) {
int n;
Scanner in = new Scanner(System.in);
n = in.nextInt();
//输入数字三角形的值
for (int i=1; i<=n; i++) {
for (int j=1; j<=i; j++) {
a[i][j]=in.nextInt(); //输入原始数据
}
}
//递推开始
for (int i=n-1; i>=1; i--) {//从最后一层逆推
for (int j=1; j<=i; j++) {
a[i][j] += Math.max(a[i + 1][j], a[i + 1][j + 1]); //路径选择
}
}
System.out.println(a[1][1]);
}
}
笔记来源:蓝桥杯省赛冲刺课程