中国商用密码算法SM4
中国商用密码算法SM4
2006年我国国家密码管理局公布了无线局域网产品使用的SM4密码算法。这是我国第一次公布自己的商用密码算法,意义重大,影响深远。这一举措标志着我国商用密码管理更加科学化和国际接轨。
SM4密码算法设计简洁,算法结构有特点,安全高效。它的公开颁布向世界展示了我国在商用密码方面的研究成果。
1. SM4算法描述
SM4算法是一个分组算法。数据分组长度为128比特,密钥长度为128比特。加密算法与密钥扩展都采用32轮迭代结构。SM4以字节(8比特)和字(32比特)位单位进行数据处理。它是对合算法,因此加解密算法相同,只是轮密钥的使用顺序相反,解密轮密钥是加密轮密钥的逆序。
1.1 基本运算
SM4算法使用模2加和循环移位作为基本运算。
1.2 基本密码部件
SM4密码算法使用了以下基本密码部件
-
S盒
SM4的S盒是一种以字节为单位的非线性代替变换,其密码学的作用是起混淆作用。S盒的输入和输出都是8位的字节。它的本质上是8位的非线性置换。例如S盒输入为EF,则取第E行第F列交点处的值进行替换。
-
非线性变换 τ \tau τ
SM4的非线性变换 τ \tau τ 是一种以字为单位的非线性变换。它由4个S盒并置构成。这里的非线性变换就和之前zuc的S盒变换原理相同,一个字有4个字节,每个字节都使用S盒进行变化,再将结果进行首尾连接。不同的是ZUC使用的是两个S盒,这里只有一个S盒。
-
线性变换 L L L
线性变换 L L L是以字为处理单位的线性变换部件,其输入输出都是32位的字。其密码学的作用是起扩散作用。
设 L L L的输入为字B,输出为字C,则:
C = L ( B ) = B ⨁ ( B < < < 2 ) ⨁ ( B < < < 10 ) ⨁ ( B < < < 18 ) ⨁ ( B < < < 24 ) C=L(B)=B\bigoplus(B<<<2)\bigoplus(B<<<10)\bigoplus(B<<<18)\bigoplus(B<<<24) C=L(B)=B⨁(B<<<2)⨁(B<<<10)⨁(B<<<18)⨁(B<<<24) -
合成变换 T T T
合成变换是由非线性变换 τ \tau τ 和线性变换L复合而成。
T ( X ) = L ( τ ( X ) ) T(X)=L(\tau(X)) T(X)=L(τ(X))
合成变换 T T T起到混淆和扩散作用,提高密码安全性。
1.3 轮函数
SM4密码算法的轮函数是一种以字为处理单位的密码函数。
设轮函数 F F F的输入为 ( X 0 , X 1 , X 2 , X 3 ) (X_0,X_1,X_2,X_3) (X0,X1,X2,X3),四个32位字,共128位。轮密钥为 r k rk rk, r k rk rk也是一个32位的字。其输出也是32位的字。
F ( X 0 , X 1 , X 2 , X 3 ) = X 0 ⨁ T ( X 1 ⨁ X 2 ⨁ X 3 ⨁ r k ) F(X_0,X_1,X_2,X_3) = X_0\bigoplus T(X_1\bigoplus X_2\bigoplus X_3\bigoplus rk) F(X0,X1,X2,X3)=X0⨁T(X1⨁X2⨁X3⨁rk)

1.4 密钥扩展算法
SM4密码使用128位的加密密钥,并采用32轮迭代加密结构,每一轮加密使用一个32位的轮密钥,共使用32个轮密钥。因此需要使用密钥扩展算法。
-
系统参数FK
在密钥扩展中使用如下的参数:
FK0=(A3B1BAC6),FK1=(56AA3350),FK2=(677D9197),FK3=(B27022DC),
-
固定参数CK
共使用32个固定参数CKi,CKi是一个字,其产生规则如下:
设cki,j 为CKi的第j字节( i = 0,1,…,31; j=0,1,2,3 ),即CKi = ( cki,0 , cki,1 , cki,2 , cki,3 ),则
c k i , j = ( 4 i + j ) × 7 ( m o d 256 ) ck_{i,j}=(4i+j)\times 7(mod 256) cki,j=(4i+j)×7(mod256)
这32个固定参数如下(16进制):00070e15 1c232a31 383f464d 545b6269 70777e85 8c939aa1 a8afb6bd 545b6269 e0e7eef5 fc030a11 181f262d 343b4249 50575e65 6c737a81 888f969d a4abb2b9 c0c7ced5 dce3eaf1 f8ff060d 141b2229 30373e45 4c535a61 686f767d 848b9299 a0a7aeb5 bcc3cad1 d8dfe6ed f4fb0209 10171e25 2c333a41 484f565d 646b7279 -
密钥扩展算法
设输入加密密钥为MK = ( MK0,MK1,MK2,MK3),输出轮密钥为 r k i rk_i rki, i = 0 , 1 , . . . , 31 i=0,1,...,31 i=0,1,...,31,中间数据为 K i K_i Ki, i = 0 , 1 , . . . , 34 , 35 i=0,1,...,34,35 i=0,1,...,34,35。则密钥扩展算法为:
-
( K 0 , K 1 , K 2 , K 3 ) = ( M K 0 ⨁ F K 0 , M K 1 ⨁ F K 1 , M K 2 ⨁ F K 2 , M K 3 ⨁ F K 3 ) (K_0,K_1,K_2,K_3)=(MK_0\bigoplus FK_0,MK_1\bigoplus FK_1,MK_2\bigoplus FK_2,MK_3\bigoplus FK_3) (K0,K1,K2,K3)=(MK0⨁FK0,MK1⨁FK1,MK2⨁FK2,MK3⨁FK3)
-
f o r ( i = 0 ; i < 32 ; i + + ) for(i=0;i<32;i++) for(i=0;i<32;i++)
r k i = K i + 4 = K i ⨁ T ′ ( K i + 1 ⨁ K i + 2 ⨁ K i + 3 ⨁ C K i ) rk_i=K_{i+4}=K_i\bigoplus T^{'}(K_{i+1}\bigoplus K_{i+2}\bigoplus K_{i+3}\bigoplus CK_i) rki=Ki+4=Ki⨁T′(Ki+1⨁Ki+2⨁Ki+3⨁CKi)
其中 T ′ T^{'} T′的变换与加密函数中的 T T T基本相同,只是将其中的线性变换 L L L修改为 L ′ L^{'} L′:
L ′ ( B ) = B ⨁ ( B < < < 13 ) ⨁ ( B < < < 23 ) L^{'}(B)=B\bigoplus (B<<<13)\bigoplus (B<<<23) L′(B)=B⨁(B<<<13)⨁(B<<<23)
分析密钥扩展算法可以发现,在算法结构方面密钥扩展算法与加密算法类似,也是采用了32轮类似的迭代处理。
特别应当注意的是在密钥扩展算法中采用了非线性变化 τ \tau τ ,这将大大加强密钥扩展的安全性。
-
2. SM4加密过程
SM4密码算法是一个分组算法。数据分组长度为128比特,密钥长度为128比特。加密算法采用32轮迭代结构,每轮使用一个轮密钥。
设输入的明文为 ( X 0 , X 1 , X 2 , X 3 ) (X_0,X_1,X_2,X_3) (X0,X1,X2,X3),输入轮密钥为 r k i rk_i rki, i = 0 , 1 , . . , 31 i=0,1,..,31 i=0,1,..,31,共32个字。输出的密文为 ( Y 0 , Y 1 , Y 2 , Y 3 ) (Y_0,Y_1,Y_2,Y_3) (Y0,Y1,Y2,Y3)。
加密算法为:
X i + 4 = F ( X i , X i + 1 , X i + 2 , X i + 3 , r k i ) = X i ⨁ T ( X i + 1 ⨁ X i + 2 ⨁ X i + 3 ⨁ r k i ) X_{i+4}=F(X_i,X_{i+1},X_{i+2},X_{i+3},rk_i)=X_i\bigoplus T(X_{i+1}\bigoplus X_{i+2}\bigoplus X_{i+3}\bigoplus rk_i) Xi+4=F(Xi,Xi+1,Xi+2,Xi+3,rki)=Xi⨁T(Xi+1⨁Xi+2⨁Xi+3⨁rki)
为了与解密算法需要的顺序一致,在加密算法之后还需要一个反序处理 R R R:
R ( Y 0 , Y 1 , Y 2 , Y 3 ) = ( X 35 , X 34 , X 33 , X 32 ) R(Y_0,Y_1,Y_2,Y_3)=(X_{35},X_{34},X_{33},X_{32}) R(Y0,Y1,Y2,Y3)=(X35,X34,X33,X32)
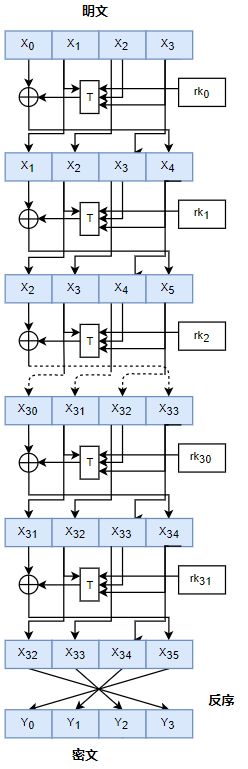
加密算法流程如下:
从图中可以看出,SM4一次加密处理4个字,产生一个字的中间密文,这个中间密文,这个中间密文与前三个字拼接在一起供下一次加处理,共迭代32轮,最终产生出四个字的密文。
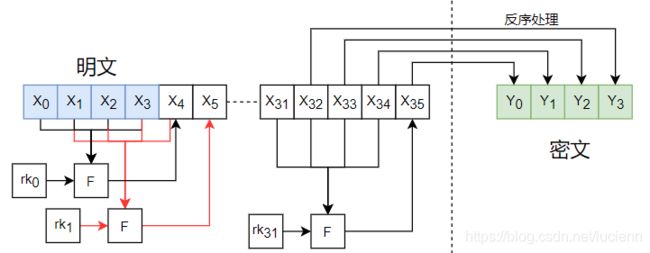
加密过程也可如下所示:
3. SM4解密过程
SM4密码算法是对合运算,因此加解密算法相同,只是轮密钥的使用顺序相反,解密轮密钥是加密轮密钥的逆序。
设输入密文为 ( Y 0 , Y 1 , Y 2 , Y 3 ) (Y_0,Y_1,Y_2,Y_3) (Y0,Y1,Y2,Y3),输入轮密钥为 r k i rk_i rki, i = 31 , 30 , . . . , 1 , 0 i=31,30,...,1,0 i=31,30,...,1,0,输出明文为 ( M 0 , M 1 , M 2 , M 3 ) (M_0,M_1,M_2,M_3) (M0,M1,M2,M3)。由 ( Y 0 , Y 1 , Y 2 , Y 3 ) = ( X 35 , X 34 , X 33 , X 32 ) (Y_0,Y_1,Y_2,Y_3)=(X_{35},X_{34},X_{33},X_{32}) (Y0,Y1,Y2,Y3)=(X35,X34,X33,X32),得解密算法为:
X i = F ( X i + 4 , X i + 3 , X i + 2 , X i + 1 , r k i ) = X i + 4 ⨁ T ( X i + 3 ⨁ X i + 2 ⨁ X i + 1 ⨁ r k i ) X_i=F(X_{i+4},X_{i+3},X_{i+2},X_{i+1},rk_i)=X_{i+4}\bigoplus T(X_{i+3}\bigoplus X_{i+2}\bigoplus X_{i+1}\bigoplus rk_i) Xi=F(Xi+4,Xi+3,Xi+2,Xi+1,rki)=Xi+4⨁T(Xi+3⨁Xi+2⨁Xi+1⨁rki)
i = 31 , 30 , . . , 1 , 0 i=31,30,..,1,0 i=31,30,..,1,0
与加密算法之后需要一个反序处理同样的道理,在解密算法之后也需要有一个反序处理 R R R:
R ( M 0 . M 1 , M 2 , M 3 ) = ( X 3 , X 2 , X 1 , X 0 ) R(M_0.M_1,M_2,M_3)=(X_3,X_2,X_1,X_0) R(M0.M1,M2,M3)=(X3,X2,X1,X0)
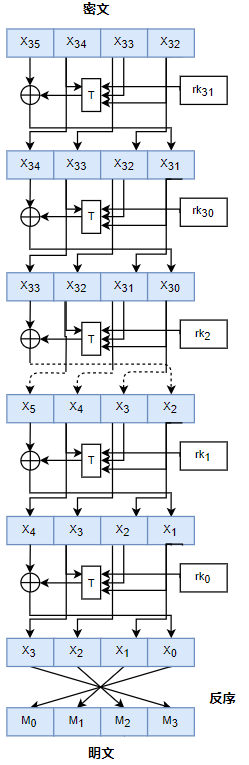
解密过程可如下所示:
4. SM4的对合性和可逆性
可逆性是对称密码算法的基本要求,对合性能够使密码算法实现的工作量减半。
4.1 SM4对合性
先分析SM4的加密轮函数,如图所示,它由两个运算组成:
加密函数G的运算可以写成:
G = G i ( X i , X i + 1 , X i + 2 , X i + 3 , r k i ) = ( X i ⨁ T ( X i + 1 , X i + 2 , X i + 3 , r k i ) , X i + 1 , X i + 2 , X i + 3 ) G=G_i(X_i,X_{i+1},X_{i+2},X_{i+3},rk_i)\\ \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad =(X_i\bigoplus T(X_{i+1}, X_{i+2}, X_{i+3}, rk_i),X_{i+1}, X_{i+2}, X_{i+3}) G=Gi(Xi,Xi+1,Xi+2,Xi+3,rki)=(Xi⨁T(Xi+1,Xi+2,Xi+3,rki),Xi+1,Xi+2,Xi+3)
则
( G i ) 2 = G i ( X i ⨁ T ( X i + 1 , X i + 2 , X i + 3 , r k i ) , X i + 1 , X i + 2 , X i + 3 , r k i ) = ( X i ⨁ T ( X i + 1 , X i + 2 , X i + 3 , r k i ) ⨁ T ( X i + 1 , X i + 2 , X i + 3 , r k i ) , X i + 1 , X i + 2 , X i + 3 , r k i ) = ( X i , X i + 1 , X i + 2 , X i + 3 , r k i ) = I (G_i)^2=G_i(X_i\bigoplus T(X_{i+1}, X_{i+2}, X_{i+3}, rk_i), X_{i+1}, X_{i+2}, X_{i+3},rk_i)\\ \quad \quad =(X_i\bigoplus T(X_{i+1}, X_{i+2}, X_{i+3}, rk_i)\bigoplus T(X_{i+1}, X_{i+2}, X_{i+3},rk_i),X_{i+1}, X_{i+2}, X_{i+3},rk_i)\\ \quad \quad=(X_i,X_{i+1},X_{i+2},X_{i+3},rk_i)\\ \quad \quad =I (Gi)2=Gi(Xi⨁T(Xi+1,Xi+2,Xi+3,rki),Xi+1,Xi+2,Xi+3,rki)=(Xi⨁T(Xi+1,Xi+2,Xi+3,rki)⨁T(Xi+1,Xi+2,Xi+3,rki),Xi+1,Xi+2,Xi+3,rki)=(Xi,Xi+1,Xi+2,Xi+3,rki)=I
I I I是恒等变换,可以看出加密函数Gi是对合运算。
数据交换E的运算可以写成:
E = ( X i + 4 , ( X i + 1 , X i + 2 , X i + 3 ) ) = ( ( X i + 1 , X i + 2 , X i + 3 ) , X i + 4 ) E=(X_{i+4},(X_{i+1},X_{i+2},X_{i+3}))=((X_{i+1},X_{i+2},X_{i+3}),X_{i+4}) E=(Xi+4,(Xi+1,Xi+2,Xi+3))=((Xi+1,Xi+2,Xi+3),Xi+4)
显然 E = E − 1 E=E^{-1} E=E−1,即 E E E是对合运算。
因此,加密轮函数可以写成:
F i = F i ( X i , X i + 1 , X i + 2 , X i + 3 , r k i ) = G i E F_i=F_i(X_i,X_{i+1},X_{i+2},X_{i+3},rk_i)=G_iE Fi=Fi(Xi,Xi+1,Xi+2,Xi+3,rki)=GiE
则加密的过程可以写成:
S M 4 = G 0 E G 1 E . . . G 30 E G 31 R SM4=G_0EG_1E...G_{30}EG_{31}R SM4=G0EG1E...G30EG31R
解密过程可以写成:
S M 4 − 1 = G 31 E G 30 E . . . G 1 E G 0 R SM4^{-1}=G_{31}EG_{30}E...G_1EG_0R SM4−1=G31EG30E...G1EG0R
比较加解密式子可以发现二者是相同的,只是密钥的使用顺序相反。这就说明SM4算法是对合运算。
4.2 SM4可逆性
加密过程可以写为:
( X 0 , X 1 , X 2 , X 3 ) (X_0,X_1,X_2,X_3) (X0,X1,X2,X3)–> ( X 1 , X 2 , X 3 , X 4 ) (X_1,X_2,X_3,X_4) (X1,X2,X3,X4)–> ( X 2 , X 3 , X 4 , X 5 ) (X_2,X_3,X_4,X_5) (X2,X3,X4,X5)–>…–> ( X 32 , X 33 , X 34 , X 35 ) (X_{32},X_{33},X_{34},X_{35}) (X32,X33,X34,X35)–> ( X 35 , X 34 , X 33 , X 32 ) (X_{35},X_{34},X_{33},X_{32}) (X35,X34,X33,X32)= ( Y 0 , Y 1 , Y 2 , Y 3 ) (Y_0,Y_1,Y_2,Y_3) (Y0,Y1,Y2,Y3)
其中最后一步为反序。
同理,解密过程可以写为:
( X 35 , X 34 , X 33 , X 32 ) (X_{35},X_{34},X_{33},X_{32}) (X35,X34,X33,X32)–> ( X 34 , X 33 , X 32 , X 31 ) (X_{34},X_{33},X_{32},X_{31}) (X34,X33,X32,X31)–> ( X 33 , X 32 , X 31 , X 30 ) (X_{33},X_{32},X_{31},X_{30}) (X33,X32,X31,X30)–>…–> ( X 3 , X 2 , X 1 , X 0 ) (X_3,X_2,X_1,X_0) (X3,X2,X1,X0)–> ( X 0 , X 1 , X 2 , X 3 ) (X_0,X_1,X_2,X_3) (X0,X1,X2,X3)
其中最后一步为反序。
由此可以得出:
S M 4 − 1 ( S M 4 ( X 0 , X 1 , X 2 , X 3 ) ) = ( X 0 , X 1 , X 2 , X 3 ) SM4^{-1}(SM4(X_0,X_1,X_2,X_3))=(X_0,X_1,X_2,X_3) SM4−1(SM4(X0,X1,X2,X3))=(X0,X1,X2,X3)
因此SM4是可逆的。