旅行推销员问题的遗传算法中的完整子路线顺序交叉
摘要
旅行商问题(TSP)是许多著名的组合问题之一。TSP可以解释为很难找到从第一个城市出发,经过所有城市,然后返回起点的最短距离。在标准问题中,TSP通常用于确定新算法的效率。遗传算法是求解TSP问题的一种成功算法。遗传算法求解效率的关键机制是交叉算子。许多研究提出了新的交叉甚至改进的解决TSP的方法,包括其他相关问题。然而,solution quality是最重要的因素。本文提出了遗传算法的完全子图阶交叉(CSOX)来搜索TSP的解。CSOX采用订单交叉Order crossover(OX)原理,并将交叉扩展到主要涵盖质量解决方案的部分。值得注意的是,一个操作可以生成六个新的解决方案。这一结果增加了问题解决方案的多样性和质量,同时降低了计算时间。从三项研究中,将五种类型的交叉算子与CSOX进行了比较。实验总结结果表明,CSOX在解决方案质量和良好的计算时间方面优于所有方案。
引言
旅行商问题(TSP)是一个常见的组合优化问题,属于NP难问题。TSP问题旨在寻找前往不同城市的最短路径。这个问题的局限性在于每个城市只能访问一次。此外,一旦访问了所有城市,销售人员必须返回出发城市。TSP经常被应用于新算法的性能评估。
遗传算法(GA)是一种受生物启发的进化算法,可以很好地解决TSP问题。遗传算法通过模仿物种的进化和自然选择的思想来工作。因此,例如,身体状况良好的生物更有可能存活下来,并将这些良好的特征传递给下一代[1]。尽管遗传算法已经提出了很长时间,但最近许多研究中开发的新算法都是在遗传算法概念之后原型化的。此外,许多研究已经应用了遗传算法原理,并将其与其他算法相结合来解决一些问题[2]。遗传算法的运作始于以染色体形式表达的群体的一代。每个染色体或个体都包含基因,代表着问题可能解决方案的一个特征。然后,遗传算法评估基因适应度,选择并相应地提高解决方案的质量。
交叉算子是解决方案改进过程中的一个重要机制。交叉通常由两个个体或两个选定的父母的组合产生。重组在父母之间进行信息交换。因此,获得的后代将具有其父母的特征。根据组合技术的不同,每个后代都会有所不同。
保持种群多样性是交叉设计的挑战之一,因为它可以防止过早收敛或陷入局部最优。此外,多样性通常会增加搜索新解决方案空间的可能性,并带来更好的解决方案质量。然而,更高的多样性是浪费时间。因此,交叉算子应该给出适当的分集,以有效地解决过早收敛问题[3]。
目前,GA有许多交叉算子。请注意,部分映射交叉(PMX)和顺序交叉(OX)是各种研究中经常发现的两种算子,用于比较和提高算法性能。PMX是使用最广泛的基于置换的交叉算子。在PMX中,第一个亲本的基因被映射到第二个亲本的遗传基因上,剩下的信息被交换。相比之下,OX通过选择第一个亲本的基因并维持第二个亲本基因的相对顺序来产生后代。尽管一些研究人员指出,PMX比OX表现出更好的解决方案搜索,但它需要更多的计算时间[4][5]。
最佳顺序交叉(BOX)是另一种将双亲和全局最佳个体之间的信息相结合的技术。该技术优于许多现有的置换交叉方案[6]。
改进(IPMX)是对PMX技术的重新设计,以减少计算时间而不影响解决方案质量。IPMX、PMX和另外两种方法进行了并行评估。最佳解决方案来自IPMX[7]。
同时,另一个选择了两个以上父母来增加多样性的运营商被称为多父母交叉。样本是多父部分映射交叉(MPPMX)和多父顺序交叉(MPOX)
因此,本研究提出了一种新的交叉算子,利用双亲产生六个后代,以按时保持种群的多样性。同时,来自父母的优秀信息将被选择传递给后代。
二、GA代表TSP
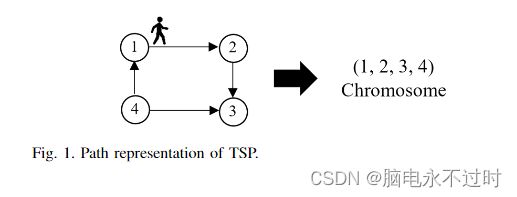
本节描述了用于解决TSP问题的遗传算法。本文对遗传算法的每一个过程进行了推广。A.染色体代表一个数字代表每个城市的名字。访问每个城市的路线或顺序是TSP的染色体编码。当一个销售人员访问所有城市时,他必须返回出发城市。路线示例1→2.→3.→4.→1可以用(1,2,3,4)表示,如图1所示。
B、 遗传算法过程在本文中,可以通过以下步骤定义一个简单的遗传算法。详情如下。第一步,创建一个由n条染色体组成的初始群体。第二步,评估每个染色体的适合度。步骤3,根据最佳适应度值选择n条染色体的群体。步骤4,使用交叉算子随机选择两个亲本来创建后代。步骤5,应用具有低随机概率的变异算子。第6步,将新的后代添加到种群中,然后进入第2步。最后,如果代数满足,则终止。步骤2中的适合度是所有城市之间旅行成本的总和。然而,TSP是一个最小化问题,因此适应度函数为F(x)=1/F(x),其中F(x)是目标函数。步骤4-5中使用的GA运算符将在第四节中讨论。
三、提出的交叉算子
本文针对TSP问题,提出了遗传算法中的完全子任务交叉(CSOX)。CSOX采用订单交叉(OX)原理,并扩展交叉位置以覆盖解决方案的适当组件。此外,还提出了保留基因序列和交换良好信息的建议。然而,CSOX在执行时间合适的情况下最多可以生成六个后代。CSOX程序在算法1中进行了描述。在图2中,OX的原理用于交换基因以产生后代。生成的子代的质量在GA工作周期的同时得到改善。通常,被选为首选旅行目的地的城市有可能提高解决方案的质量,因为这些城市通常位于起点和最后一个城市附近。
因此,将选择排名第一和最后的城市,以进一步传播给具有这一概念的后代。
四、实验和结果
在本节中,实验分为四个部分,以评估CSOX与TSP实例中其他交叉的效果。本研究采用了TSPLIB,这是一个著名的TSP实例库(可从http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/)。
实验1-3是与关于解决方案的其他文献相比的CSOX功效评估。 travel costs函数衡量解决方案的质量,最优解决方案的 travel costs最低。根据对比研究调整各实验的参数设置。此外,各文献中使用的TSP实例并不相等。只有在所有实例中发现相同的实例才会被选中。例如,eil51、st70,实例名称上的数字表示城市的数量。最后,实验4是与广泛已知的交叉相比的CSOX收敛性评估。所提出的算法用python编程语言实现,并在装有Windows 10操作系统、2.60 GHz Intel i7处理器和8 GB RAM的笔记本电脑上运行。
实验一:
本实验将CSOX的性能与BOX和OX[6]进行了比较。参数设置和比较结果分别如表I-II所示:
从表II可以看出,CSOX在所有情况下都给出了比BOX和OX更好的最佳值、平均值。尽管BOX和OX没有显示最差值,但CSOX的最差值优于BOX和OX的最佳值。
B.实验2
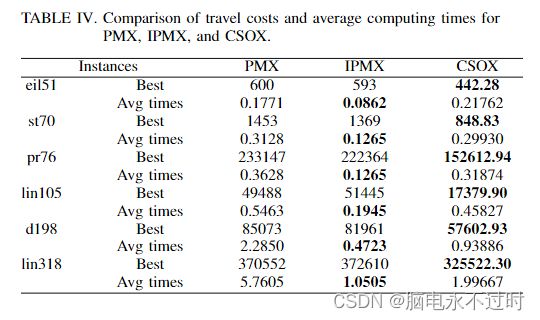
本实验比较了CSOX与PMX和IPMX[7]在解决方案质量和计算时间方面的性能。参数设置和比较结果分别如表III-IV所示。
在表IV中,PMX和IPMX在溶液质量方面表现出相似之处。然而,IPMX工作速度更快,而CSOX提供的解决方案质量比PMX和IPMX更好。在计算时间方面,CSOX比PMX消耗的时间更少,并且提供了更好的解决方案质量。
C.实验3
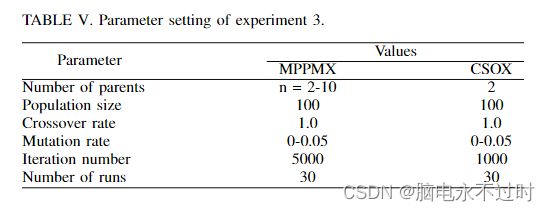
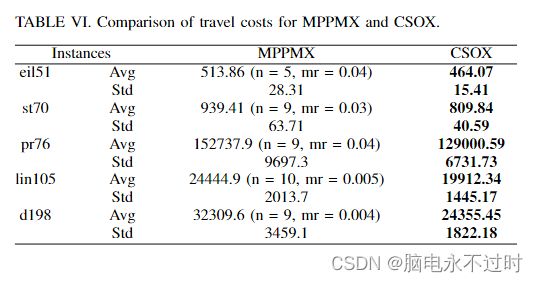
本实验比较了CSOX与MPPMX和MPOX的性能。不幸的是,对上述发布的实验数据进行了检查。发现数据不准确,并且偏离了TSP实例的标准解,因此无法进行比较。因此,本实验将CSOX与MPPMX[8]进行了比较。参数设置和比较结果分别如表V-VI所示。
这个实验使用了交换突变以及MMPMX。如表VI所示,基于参考数据,MPPMX疗效测试仅使用了五个实例。CSOX的突变率为0.03,在所有情况下都比MPPMX的结果更好。
D.实验4
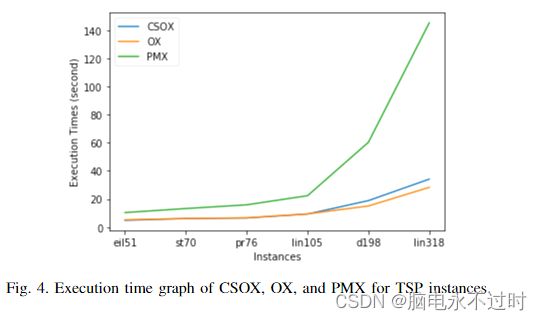
最后的实验比较了CSOX、OX和PMX的收敛性。不幸的是,这个实验无法与以前实验中的算法进行比较,以防止结果出现错误。参数设置如下:种群规模=500,交叉率=1.0,突变率=0.0,运行次数=30。
图3显示了解的收敛性,它对应于TSP实例的生成数量。同样,CSOX的收敛性能优于PMX和OX,包括解决方案质量。CSOX最多可产生六个后代,这对其他运营商来说是有利的,这是一种不公平的测试。因此,执行时间是该测试的度量标准。该实验定义了满足解决方案时的终止条件,以评估执行时间。
定义操作员遇到的终止条件,以评估执行时间。终止条件是三个运算符的最低平均解,即PMX。
从图4中可以看出,对于eil51、st70、pr76和lin105,CSOX和OX的执行时间相似。相比之下,d198和lin318的OX执行时间更短。PMX在所有实例中具有最多的执行时间。
V.结论
CSOX是一种基于遗传算法的新阶交叉算子,用于求解TSP问题。就解决方案质量而言,CSOX可以比其他交叉运营商产生更好的结果。最重要的是,在任何实验中都没有使用突变算子。尽管CSOX最多能产生六个后代,但计算时间并不高。此外,CSOX在其他TSP实例中进行了测试,并在许多实例中表现良好