【贪心专题】—— 贪心算法入门篇

贪心算法入门

一、什么是贪心算法

• “贪心算法（greedy algorithm，又称贪婪算法）是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，算法得到的是在某种意义上的局部最优解。”

• 贪心的本质是选择每一阶段的局部最优，从而达到全局最优。

• 贪心算法没有固定的框架，算法设计的关键是贪婪策略的选择。

二、使用贪心算法的一般步骤

有点与动态规划类似，这就导致了我们有些题很难想出来是应该用贪心还是动态规划。

• 将问题划分为若干个子问题
• 找出适合的贪心策略
• 求解每一个子问题的最优解
• 将局部最优解堆叠成全局最优解

案例分析

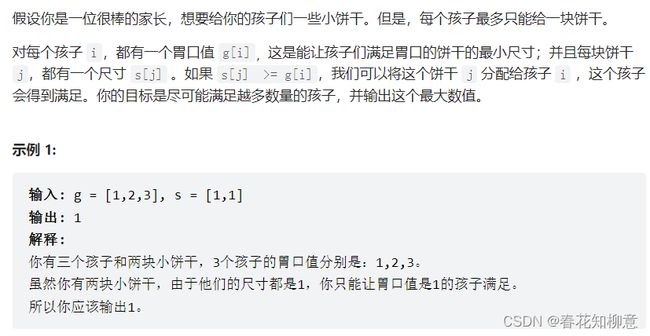
一、分发饼干问题

• 问题描述:
  
  贪心算法就是一个通过局部最优来求整体最优的过程

此题有两个解决方向，将大饼干给胃口大的孩子 或 将小饼干给胃口小的孩子来获得最优解

贪心策略：将两个数组排序【利用Arrays.sort()方法】
采用大饼干先分给胃口大的孩子方案，就从后向前遍历两个数组；
选择另一种方案就从前向后遍历数组

• Java版本的两种算法：

class Solution {
	//先分发小饼干
    public int findContentChildren(int[] g, int[] s) {
        int count = 0;
        //排序
        Arrays.sort(g);
        Arrays.sort(s);

        //双层for循环，来判断当前的饼干是否可以满足孩子
        for(int i = 0, j = 0; i < s.length && j < g.length; ){
            if(s[i] >= g[j]){
                j++;
                count++;
            }
            i++;
        }
        return count;
    }
}

在最开始的版本中，我将计数器定义在了全局变量的位置，并声明为静态变量
static int count = 0;
就出现了下面的这两种情况：

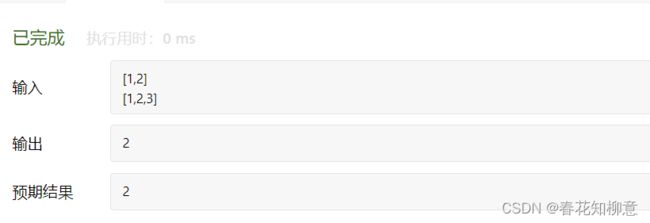
在同一组数据的前提下，测试时是可以通过的，但是在提交时就是错误的

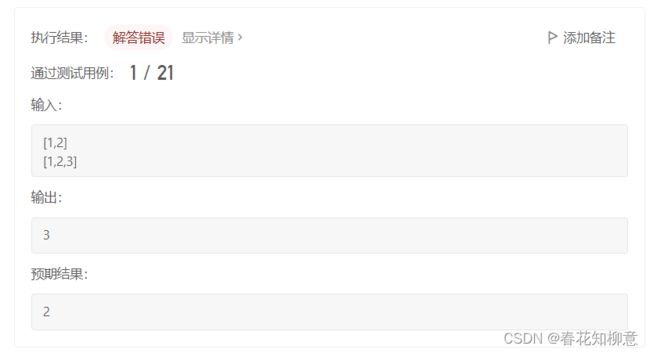
这里是一个关于LeetCode编辑器的一个坑，leetcode的判定规则：每次提交后所用的测试用例共享全局变量和类变量。

测试的时候用例只有一个，而提交相当于测试很多个用例，这些用例共享所有的静态变量，某个变量使用到的静态变量可能被上一个测试用例修改过了，就会出现问题。

总之，LeetCode做题不要用静态变量

class Solution {
    //大饼干先分给胃口大的孩子
    public int findContentChildren(int[] g, int[] s) {
        int count = 0;
        //排序
        Arrays.sort(g);
        Arrays.sort(s);

        //大饼干给胃口大的孩子
        for(int i = s.length - 1, j = g.length - 1; i >= 0 && j >= 0;  ){
            if(s[i] >= g[j]){
                i--;
                count++;
            }
            j--;
        }
        return count;
    }
}

---

二、摆动序列问题

• 问题描述：
  
  如果创建二维直角坐标系，横坐标为数组nums的索引，纵坐标为对应的元素值
  
  局部最优：删除坡度上的结点，只保留坡度两端的点，这个坡度上又两个局部峰值
  整体最优：使序列中具有最多的局部峰值，从而获得最长摆动序列。

• Java版本：

class Solution {
    public int wiggleMaxLength(int[] nums) {
        //数组只有一个元素
        if(nums.length == 1) {
            return 1;
        }

        //创建保存当前坡度和前一段坡度的变量
        int preDiff = 0;
        int curDiff = 0;
        
        //创建保存子序列包含的点个数的变量【子序列的长度】
        int res = 1; //因为此时数组的长度至少为2， nums[0]=nums[1]时
        
        //遍历数组
        for(int i = 0; i < nums.length - 1; i++){
            curDiff = nums[i + 1] - nums[i];
            //因为当前坡度为零的话没有统计意义
            if((curDiff > 0 && preDiff <= 0) || (curDiff < 0 && preDiff >= 0)){
                res++;
               preDiff = curDiff; 
            }
                   
        }

        //返回结果
        return res;
    }
}

---

三、最大子数组和问题

• 问题描述：
  

贪心篇：明确局部最优是什么，整体最优又是什么，选择合适的贪心策略

局部最优: 当前连续和是正的
整体最优：选取最大的连续和

首先，我们要知道一个问题，如果连续和为负数，那么这个子序列我们是不能要的，要从此子序列后面的子序列考虑最大子数组和

例： 1 2 3 - 7 1 前四个数的和为负数，无论我们从数组下标 0-3
哪出开始算起，这部分加到最大子数组中都是产生副作用的（和值小于零）
所以我们应该从索引4开始重新考虑

• Java版本：

class Solution {
    public int maxSubArray(int[] nums) {
        
        //设置保存最大子数组和值的变量
        int maxNum = Integer.MIN_VALUE;

        //记录当前子序列和值的变量
        int count = 0;
        
        //遍历数组
        for(int i = 0; i < nums.length; i++){
            count += nums[i];

            //如果当前子序列的和值大于最大子序列的和值，就更新最大子序列的和值
            if(count > maxNum){
                maxNum = count;
            }

            //如果当前和值为负数了，那么新的子序列和值应该为其后面的子序列
            if(count < 0){
                count = 0;
            }
        }
        
        //返回结果
        return maxNum;
    }
}

---

四、买股票的最佳时机 II

• 问题描述：
  

我们可以发现，在这个问题中股票可以在当天买入，当天卖出，而且可以交易股票多次

假设： prices = [1, 2, 3, 4] 我们很容易得知，在第一天买入、第四天卖出可以获得最大的利润3.

一次交易最近的区间为两天，因为当天买入当天卖出没有任何的意义
选择第一天买入第四天卖出是因为我们知道第一天股票价格最低，第四天股票的价格最高
可以看成: 第一天买第二天卖、第二天买第三天卖、第三天卖、第四天卖
4 - 1 = (2 - 1) + (3 - 2) + (4 - 3)

因为上边是股票价格递增的，但实际如果不是递增的，就要分为多次交易来决定总利润。

局部最优：获取正利润
整体最优: 所有正利润的和

所以，假设每两天进行一次交易，如果利润为正值，就进行交易，否则不买入也不售出股票

• java版本代码：

class Solution {
    public int maxProfit(int[] prices) {

        int maxProfit = 0;

        for(int i = 0; i < prices.length - 1; i++){
            int countProfit = prices[i + 1] - prices[i];
            if( countProfit > 0){
                maxProfit += countProfit;
            }
        }

        return maxProfit;        
    }
}

---

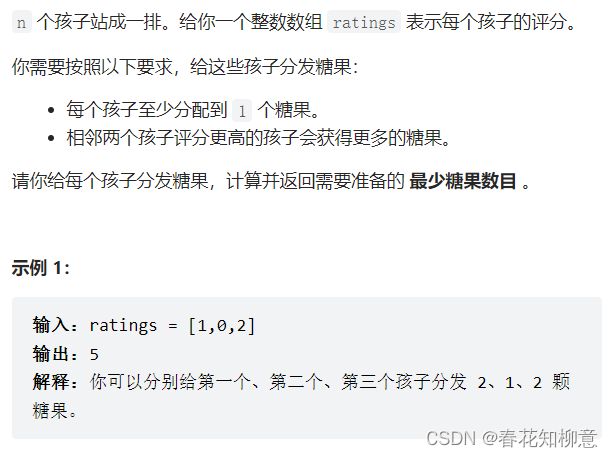
五、分发糖果问题

• 题目描述：
  

假设孩子 i 两边都有孩子，那么他/她就要和两边的孩子比较来确定他/她应该获得多少个糖果。

整个过程分为两部分：从前向后的遍历和从后向前的遍历

️ 从前向后遍历，右边评分大于左边，ratings[i] 与 ratings[i - 1]比较

谁大谁获得更多的糖果，candyNum[i] 为第 i 个孩子应
该得到的糖果，此时的贪心策略为：
candyNum[i] = ratings[i] > ratings[i - 1] ? candyNum[i-1] + 1 : 1;

️ 从后向前遍历，左边评分大于右边，ratings[i] 与 ratings[i + 1]比较

还是大着获得更多的糖果，此时candyNum的贪心策略为
candyNum[i] = Math.max(candyNum[i+1]+1, candyNum[i]);

⭕️ 最后再遍历 candyNum[i],将每个孩子所需要的糖果数加和，就得到了最少糖果数目

• Java版本代码:

class Solution {
    public int candy(int[] ratings) {

        //获得孩子的个数
        int num = ratings.length;

        //保存结果的变量
        int res = 0;

        //创建保存每个孩子所需要的糖果数的数组
        int [] candyNum = new int [num];
        
        //设置初始值
        candyNum[0] = 1;
        
        //从前向后遍历
        for(int i = 1; i < num; i++){
            
            candyNum[i] = ratings[i] > ratings[i - 1] ? candyNum[i-1] + 1 : 1;
            
        }

        //从后向前遍历
        for(int i = num - 2; i >= 0; i--){
            if(ratings[i] > ratings[i + 1]){
                candyNum[i] = Math.max(candyNum[i+1]+1, candyNum[i]);
            }
        }

        //遍历数组candyNum，获得需要的最少糖果数目
        for(int i = 0; i < num; i++){
            res += candyNum[i];
        }

        //返回结果
        return res;
    }
}