【数据结构】二叉树的遍历 - 动图演示

---

前言

如果你还不知道树及二叉树的概念，请先看这篇文章树和二叉树的介绍

对于二叉树，我们学习的重点是二叉树的结构，而想要学好二叉树的结构，则离不开二叉树的基本操作-二叉树的遍历，二叉树的遍历则离不开递归。因此本文将为你介绍如何进行二叉树的遍历，以及如何更好的理解与使用递归。

---

一、二叉树的遍历

概念：所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。由于二叉树的结构天然满足递归的使用条件，因此二叉树的遍历通常由递归来完成。 遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。

注：递归
递归是一种编程技巧，它定义了一个问题的解决方案，该方案可以通过调用自身来解决更小的同类问题并最终得出问题的解决方案。
递归通常在以下情况下使用：

1. 问题可以被分割为更小的同类问题，且每个子问题可以使用相同的解决方案。
2. 问题的规模或深度未知或非常大，无法使用迭代或其他方法解决。
3. 代码的可读性和简洁性比代码效率更为重要时，使用递归可以更容易地实现算法。

由二叉树的定义可知，一个二叉树也是由二叉树组成,一个节点是根节点，同时也可能是左/右孩子节点，这刚好符合递归的第一种使用情况。

1.1 创建二叉树

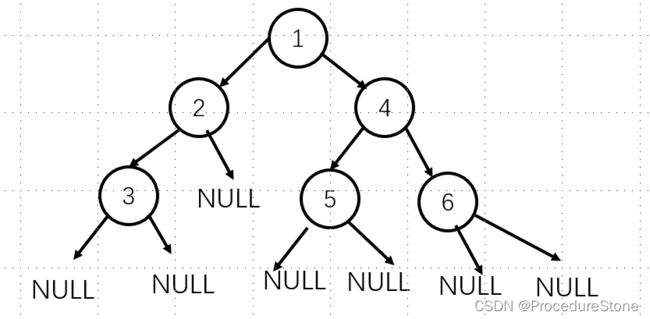
要进行二叉树的遍历，首先我们要先创建一颗二叉树。由于二叉树的创建也是建立在遍历的基础上，所有现在我们先手动创建一颗树。

typedef int BTDataType;
typedef struct BinaryTreeNode//Binary 意思为 二叉，二进制
{
	BTDataType val;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

BTNode* BuyNode(int x) {
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	assert(newnode);
	newnode->val = x;
	newnode->left = NULL;
	newnode->right = NULL;
	return newnode;
}
BTNode* CreatBinaryTree()
{
	BTNode* node1 = BuyNode(1);
	BTNode* node2 = BuyNode(2);
	BTNode* node3 = BuyNode(3);
	BTNode* node4 = BuyNode(4);
	BTNode* node5 = BuyNode(5);
	BTNode* node6 = BuyNode(6);
	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;
	return node1;
}
int main(void) {
	BTNode* root = CreatBinaryTree();
}

---

二叉树创建好后，就要开始进行二叉树的遍历了。

1.2 二叉树的遍历方式

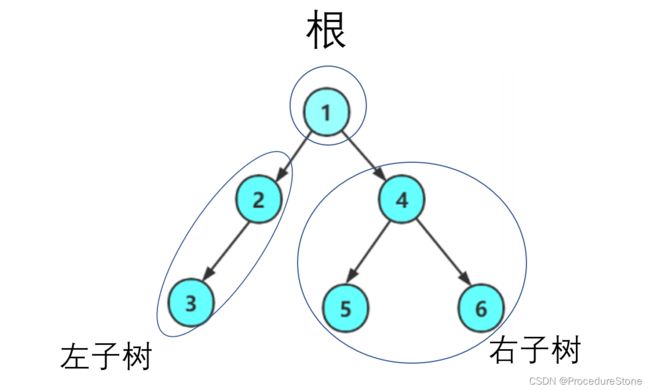
我们对于一个二叉树，要将它看作三部分构成：根，左子树，右子树
注：根，左子树，右子树是相对的。例如：2相对于1是左子树，5相对于4是左子树。

根据访问这三部分的先后顺序，可以分为以下三种遍历方式，它们的名称及访问顺序如下

• 前序遍历（PreOrder）：根，左子树，右子树
• 中序遍历（InOrder）：左子树，根，右子树
• 后序遍历（PostOrder）：左子树，右子树，根

除此之外还有一种遍历方式：
层次遍历（LevelOrder） ： 第一层，第二层，第三层……

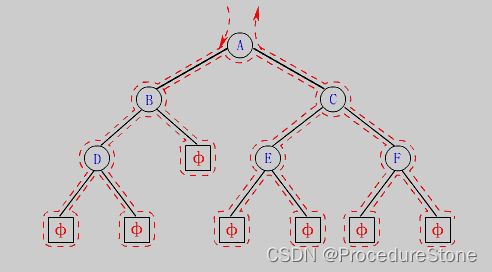
为了更好的理解它们的含义，下面我们采用动画的形式来演示如何进行前序遍历？

因此前序遍历的结果（省去NULL）为 1 2 3 4 5 6
那中序遍历，后续遍历，层序遍历的结果呢？读者不妨先自己动手写一下。

中序遍历：NULL 3 NULL 2 NULL 1 NULL 5 NULL 4 NULL 6 NULL 即 3 2 1 5 4 6
后序遍历：NULL NULL 3 NULL 2 NULL NULL 5 NULL NULL 6 4 1 即 3 2 5 6 4 1
层序遍历：1 2 4 3 NULL5 6

---

1.3 二叉树遍历的实现

现在我们已经知道如何进行二叉树的遍历。那怎么用代码来实现呢？在文章开头我们就提到二叉树的遍历需要使用递归，具体代码如下：

以前序遍历为例：

void PreOrder(BTNode* root) {
	//递归的终止条件
	if (root == NULL) {
		printf("NULL ");
		return;
	}
	//我们使用打印来表示访问
	printf("%d ", root->val);
	PreOrder(root->left);
	PreOrder(root->right);
}
//打印结果为：1 2 3 NULL NULL NULL 4 5 NULL NULL 6 NULL NULL

递归的代码很简洁，但对于新手理解起来有一定难度，我们可以通过画递归展开图来进行理解。
（动图制作不易，麻烦点个赞）


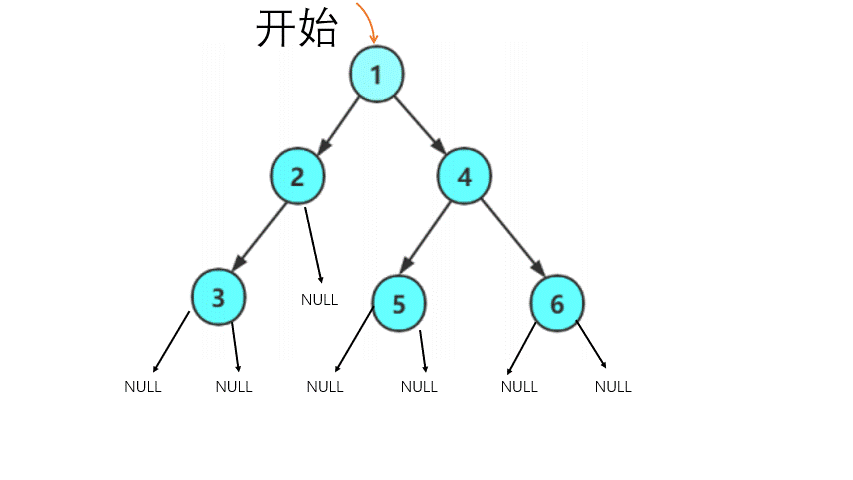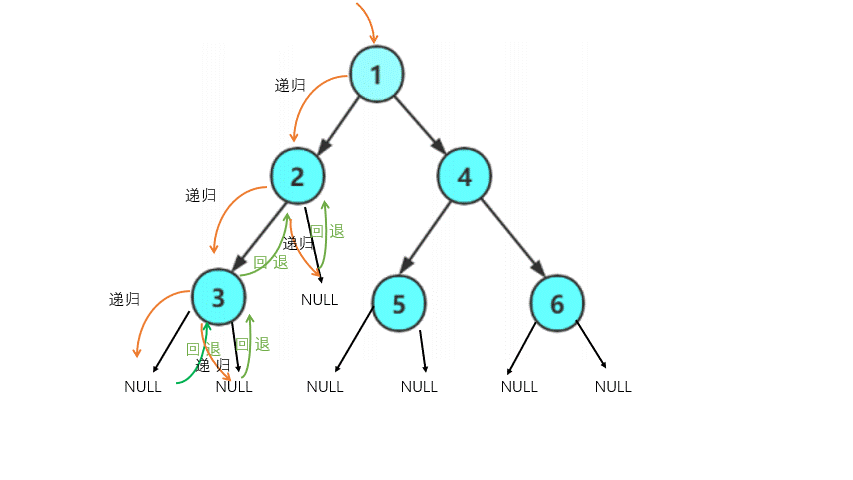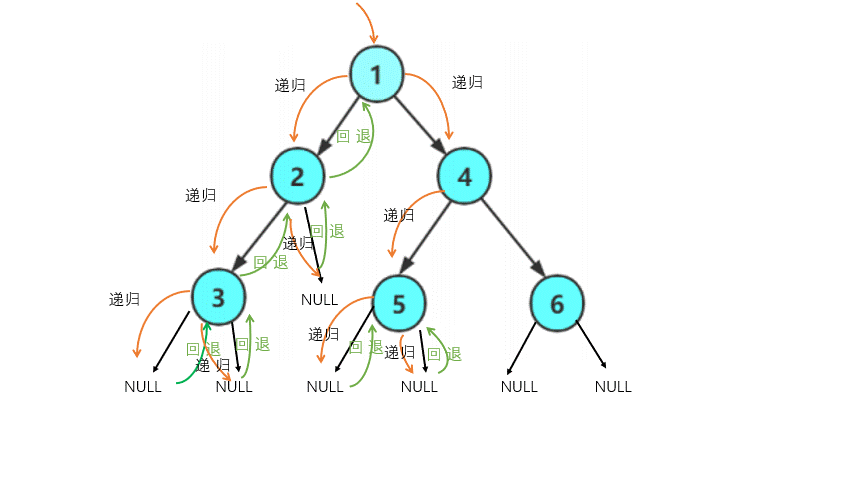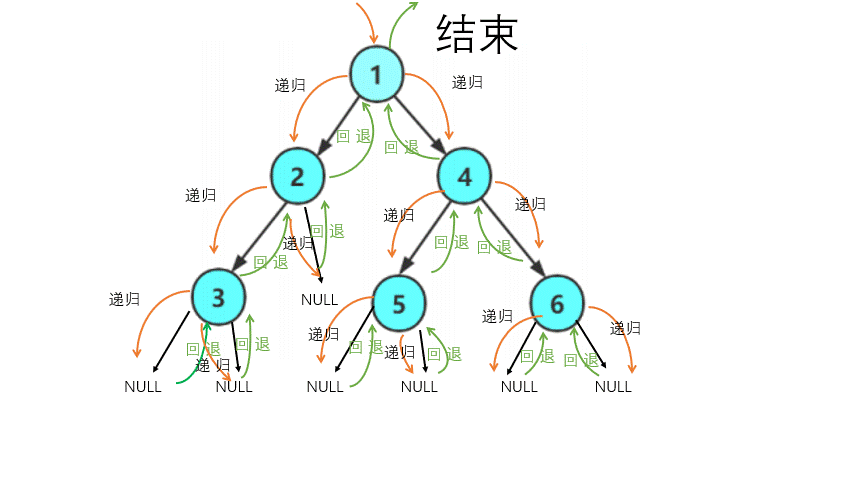
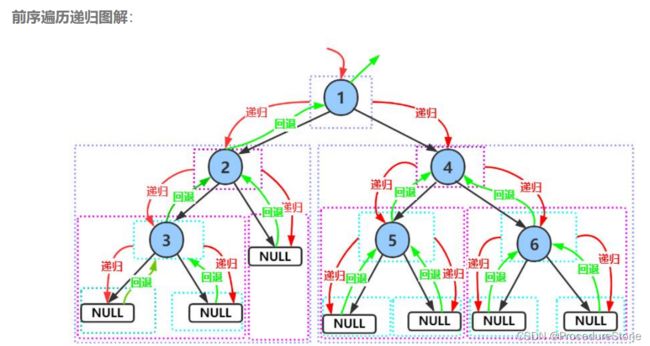
同理，你能写出中序遍历和后序遍历的代码（至于层序遍历，它需要用到队列）

//中序遍历
void InOrder(BTNode* root) {
	if (root == NULL) {
		printf("NULL ");
		return;
	}
	InOrder(root->left);
	printf("%d ", root->val);	
	InOrder(root->right);
}
//后序遍历
void PostOrder(BTNode* root) {
	if (root == NULL) {
		printf("NULL ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->val);
}

---

二、二叉树的其他操作

// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 层序遍历
int LevelOrder(BTNode* root, int k)

上述操作也离不开递归，但它们其中所用到算法思想并不是遍历，而是采用的分治。至于为什么？我将在下一篇博客【数据结构】二叉树的分治中予以解释。（目前还未写出）

---

在二叉树的遍历中，了解前序遍历、中序遍历、后序遍历等基本概念，以及它们的应用场景和实现方式是非常重要的。希望本文对读者有所启发，增加对二叉树遍历的理解和掌握，并能够通过实践提高自己的编程能力。在日后的学习和工作中，相信这些知识点会为您带来更多的便利和帮助。