GAMES101-现代计算机图形学学习笔记(作业01)
GAMES101-现代计算机图形学学习笔记(作业01)
Assignment 01
-
- GAMES101-现代计算机图形学学习笔记(作业01)
- 作业
-
- 作业描述
- 需要补充的函数
- 思路
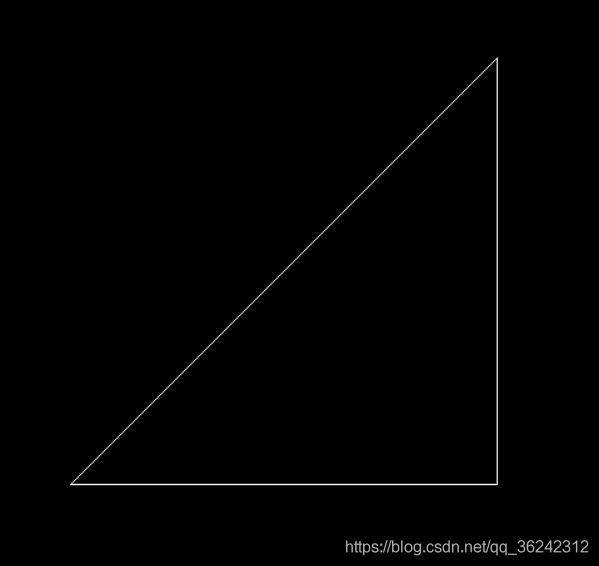
- 结果
原课程视频链接以及官网
b站视频链接: link.
课程官网链接: link.
作业
作业描述
本次作业的任务是填写一个旋转矩阵和一个透视投影矩阵。给定三维下三个 点
v0(2.0,0.0,−2.0),
v1(0.0,2.0,−2.0),
v2(−2.0,0.0,−2.0),
你需要将这三个点的坐标变换为屏幕坐标并在屏幕上绘制出对应的线框三角形 (在代码框架中,我们已经提供了 draw_triangle 函数,所以你只需要去构建变换矩阵即可)。简而言之, 我们需要进行模型、视图、投影、视口等变换来将三角形显示在屏幕上。在提供的代码框架中,我们留下了模型变换和投影变换的部分给你去完成。
提高篇: 在 main.cpp 中构造一个函数,该函数的作用是得到绕任意过原点的轴的旋转变换矩阵。
需要补充的函数
get_model_matrix(float rotation_angle): 逐个元素地构建模型变换矩阵并返回该矩阵。在此函数中,你只需要实现三维中绕 z 轴旋转的变换矩阵,而不用处理平移与缩放。
get_projection_matrix(float eye_fov, float aspect_ratio, float zNear, float zFar):使用给定的参数逐个元素地构建透视投影矩阵并返回该矩阵。
思路
①model 变换
model矩阵是MVP变换中的第一个矩阵,它用于将物体从自身局部坐标变换到世界坐标,题目要求实现三维中绕z轴旋转的变换矩阵和任意轴旋转的变换矩阵。
对于绕z轴旋转的变换矩阵有如下特点:
R z ( α ) = ( cos α − sin α 0 0 sin α cos α 0 0 0 0 1 0 0 0 0 1 ) \mathbf{R}_{z}(\alpha)=\left(\begin{array}{cccc} \cos \alpha & -\sin \alpha & 0 & 0 \\ \sin \alpha & \cos \alpha & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) Rz(α)=⎝⎜⎜⎛cosαsinα00−sinαcosα0000100001⎠⎟⎟⎞
Eigen::Matrix4f get_model_matrix(float rotation_angle)
{
Eigen::Matrix4f model = Eigen::Matrix4f::Identity();
Eigen::Matrix4f rotate(4,4); // z-axis rotation
float radian = rotation_angle / 180.0 * MY_PI;
rotate << cos(radian), -sin(radian), 0, 0,
sin(radian), cos(radian), 0, 0,
0, 0, 1, 0,
0, 0, 0, 1;
model = rotate * model;
return model;
}
而如果想要实现任意轴旋转,我们需要先得到一个交于原点的旋转轴和旋转角度,得到了之后只需要根据轴角公式旋转即可:
R ( n , α ) = cos ( α ) I + ( 1 − cos ( α ) ) n n T + sin ( α ) ( 0 − n z n y n z 0 − n x − n y n x 0 ) ⏟ N \mathbf{R}(\mathbf{n}, \alpha)=\cos (\alpha) \mathbf{I}+(1-\cos (\alpha)) \mathbf{n} \mathbf{n}^{T}+\sin (\alpha) \underbrace{\left(\begin{array}{ccc} 0 & -n_{z} & n_{y} \\ n_{z} & 0 & -n_{x} \\ -n_{y} & n_{x} & 0 \end{array}\right)}_{\mathbf{N}} R(n,α)=cos(α)I+(1−cos(α))nnT+sin(α)N ⎝⎛0nz−ny−nz0nxny−nx0⎠⎞
Eigen::Matrix4f get_model_matrix_axis(float rotation_angle, Eigen::Vector3f axis_start, Eigen::Vector3f axis_end)
{
// Eigen::Vector3f axis_start 为起点
// Eigen::Vector3f axis_end 为终点
Eigen::Matrix4f model = Eigen::Matrix4f::Identity();
// normalize axis
Eigen::Vector3f axis;
axis[0] = axis_end[0] - axis_start[0];
axis[1] = axis_end[1] - axis_start[1];
axis[2] = axis_end[2] - axis_start[2];
float norm = sqrt(axis[0] * axis[0] + axis[1] * axis[1] + axis[2] * axis[2]);
axis[0] /= norm;
axis[1] /= norm;
axis[2] /= norm;
// compute radian
float radian = rotation_angle / 180.0 * MY_PI;
// compute component 计算轴角旋转矩阵分量
Eigen::Matrix3f n(3, 3);
n << 0, -axis[2], axis[1],
axis[2], 0, -axis[0],
-axis[1], axis[0], 0;
Eigen::Matrix3f component1 = Eigen::Matrix3f::Identity() * cos(radian);
Eigen::Matrix3f component2 = axis * axis.transpose() * (1 - cos(radian));
Eigen::Matrix3f component3 = n * sin(radian);
Eigen::Matrix3f rotate_m = component1 + component2 + component3;
// Eigen 自带构造轴角旋转矩阵
// 下列注释用于验证我们构造的轴角旋转矩阵是否和Eigen的构造的轴角旋转矩阵一致
//Eigen::AngleAxisf rotation_vector(radian, Vector3f(axis[0], axis[1], axis[2]));
//Eigen::Matrix3f rotation_matrix;
//rotation_m = rotation_vector.toRotationMatrix();
Eigen::Matrix4f rotate_martix = Eigen::Matrix4f::Identity();
rotate_martix.block(0, 0, 3, 3) = rotate_m; // 前三个维度为旋转矩阵
model = rotate_martix * model;
return model;
}
②view变换
view变换用于计算相机视角,这里采用透视投影的方式,第一步先计算M_persp2ortho矩阵,用于将视锥挤压成长方体,第二步计算M_ortho,即将长方体内的坐标进行投影,最后一步通过两次变换即可计算出最终的透视投影矩阵。
Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio,
float zNear, float zFar)
{
Eigen::Matrix4f projection = Eigen::Matrix4f::Identity();
Eigen::Matrix4f M_persp2ortho(4, 4);
Eigen::Matrix4f M_ortho_scale(4, 4);
Eigen::Matrix4f M_ortho_trans(4, 4);
//已更正
float angle = eye_fov * MY_PI / 180.0;
float height = zNear * tan(angle) * 2;
float width = height * aspect_ratio;
auto t = -zNear * tan(angle / 2); // 上截面
auto r = t * aspect_ratio; //右截面
auto l = -r; // 左截面
auto b = -t; // 下截面
// 透视矩阵"挤压"
M_persp2ortho << zNear, 0, 0, 0,
0, zNear, 0, 0,
0, 0, zNear + zFar, -zNear * zFar,
0, 0, 1, 0;
// 正交矩阵-缩放
M_ortho_scale << 2 / (r - l), 0, 0, 0,
0, 2 / (t - b), 0, 0,
0, 0, 2 / (zNear - zFar), 0,
0, 0, 0, 1;
// 正交矩阵-平移
M_ortho_trans << 1, 0, 0, -(r + l) / 2,
0, 1, 0, -(t + b) / 2,
0, 0, 1, -(zNear + zFar) / 2,
0, 0, 0, 1;
Eigen::Matrix4f M_ortho = M_ortho_scale * M_ortho_trans;
projection = M_ortho * M_persp2ortho * projection;
return projection;
}