python中dot函数_Python 的NumPy 库中dot()函数详解
Python的NumPy库中dot()函数详解
本人在学习Python数据分析时的线性代数运算章节中,遇到矩阵乘法的dot函数的用法一时难于理解,后来,经查阅其他博主的相关资料,总结详解如下
1、NumPy库中dot()函数语法定义:
importnumpy as np
np.dot(a, b, out=None) #该函数的作用是获取两个元素a,b的乘积.
2、前面讲过数组的运算是元素级的,数组相乘的结果是各对应元素的积组成的数组,而对于矩阵而言,需要求的是点积,这里NumPy库提供了用于矩阵乘法的dot函数。在jupyter notebook中执行的代码运算如下:
![]()
![]()
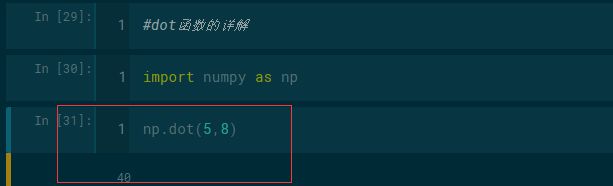
#dot函数的详解
importnumpy as np
np.dot(5,8)#如果arr1和arr都是一维数组,那么它返回的就是向量的内积。
arr1 = np.array([2,3])
arr1
array([2, 3])
arr2= np.array([4,5])
arr2
array([4, 5])
np.dot(arr1,arr2)
arr3= np.array([2,3,4])
arr3
array([2, 3, 4])
arr4= np.array([5,6,7])
arr4
array([5, 6, 7])
np.dot(arr3,arr4)#如果arr5和arr6都是二维数组,那么它返回的是矩阵乘法。
arr5 = np.array([[2,3],[4,5]])
arr5
array([[2, 3],
[4, 5]])
arr6= np.array([[6,7],[8,9]])
arr6
array([[6, 7],
[8, 9]])
np.dot(arr5,arr6)
array([[36, 41],
[64, 73]])
arr7= np.array([[2,3,4],[5,6,7]])
arr7
array([[2, 3, 4],
[5, 6, 7]])
arr8= np.arange(9).reshape(3,3)
arr8
array([[0,1, 2],
[3, 4, 5],
[6, 7, 8]])
np.dot(arr7,arr8)
array([[33, 42, 51],
[60, 78, 96]])
arr9= np.arange(6).reshape(3,2)
arr9
array([[0,1],
[2, 3],
[4, 5]])
np.dot(arr7,arr9)
array([[22, 31],
[40, 58]])
np.dot(arr8,arr9)
array([[10, 13],
[28, 40],
[46, 67]])
arr10= np.arange(6).reshape(2,3)
arr10
array([[0,1, 2],
[3, 4, 5]])
arr11= np.arange(9).reshape(3,3)
arr11
array([[0,1, 2],
[3, 4, 5],
[6, 7, 8]])
np.dot(arr10,arr11)
array([[15, 18, 21],
[42, 54, 66]])
arr12= np.arange(12).reshape(4,3)
arr12
array([[ 0,1, 2],
[3, 4, 5],
[6, 7, 8],
[9, 10, 11]])
arr13= np.arange(9).reshape(3,3)
arr13
array([[0,1, 2],
[3, 4, 5],
[6, 7, 8]])
np.dot(arr12,arr13)
array([[15, 18, 21],
[42, 54, 66],
[69, 90, 111],
[96, 126, 156]])
arr14= np.arange(15).reshape(3,5)
arr14
array([[ 0,1, 2, 3, 4],
[5, 6, 7, 8, 9],
[10, 11, 12, 13, 14]])
np.dot(arr12,arr14)
array([[25, 28, 31, 34, 37],
[70, 82, 94, 106, 118],
[115, 136, 157, 178, 199],
[160, 190, 220, 250, 280]])
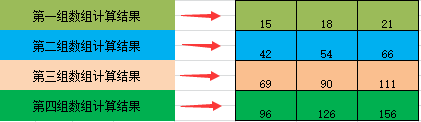
dot函数的运算总代码显示如下
3、这样的多维数组矩阵运算,通过Python代码来实现倒是挺方便的,但是,通过我们人眼看起来,对于刚入门的朋友来说,可能会很吃力,或者不清楚该结果是怎么实现的,接下来,我给大家一一介绍一下运算过程。
4、如下单个数的dot函数运算所示:
np.dot(5,8)40
5、如下一维数组的dot函数运算所示:
![]()
![]()
#如果arr1和arr都是一维数组,那么它返回的就是向量的内积。
arr1 = np.array([2,3])
arr1
array([2, 3])
arr2= np.array([4,5])
arr2
array([4, 5])
np.dot(arr1,arr2)23arr3= np.array([2,3,4])
arr3
array([2, 3, 4])
arr4= np.array([5,6,7])
arr4
array([5, 6, 7])
np.dot(arr3,arr4)56
一维数组的代码案例如下
利用表格计算法来解释上面的一维数组乘积的结果计算过程如下表1,表2,所示:
表 1 表 2
通过上表中的计算过程显示,是不是很快就能清楚,矩阵之间的运算。从而快速了解运算结果的由来。
6、如下二维数组的dot函数运算所示:
二维数组矩阵之间的dot函数运算得到的乘积是矩阵乘积
![]()
![]()
#如果arr5和arr6都是二维数组,那么它返回的是矩阵乘法。
arr5 = np.array([[2,3],[4,5]])
arr5
array([[2, 3],
[4, 5]])
arr6= np.array([[6,7],[8,9]])
arr6
array([[6, 7],
[8, 9]])
np.dot(arr5,arr6)
array([[36, 41],
[64, 73]])
二维数组的代码案例如下
利用表格计算法来解释上面的,二维数组乘积的结果计算过程如下表3,所示:
表 3
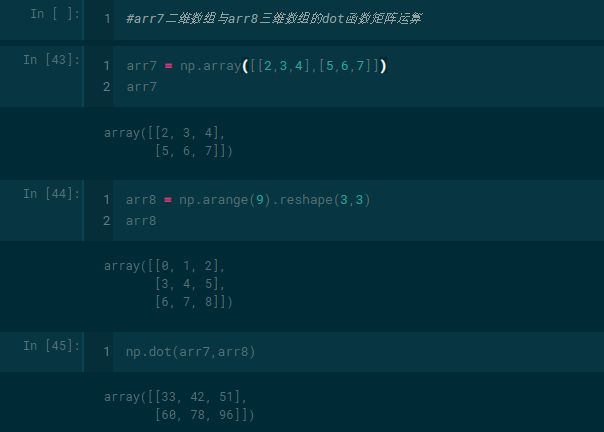
7、如下二维数组与三维数组的dot函数运算:
![]()
![]()
#arr7二维数组与arr8三维数组的dot函数矩阵运算
arr7 = np.array([[2,3,4],[5,6,7]])
arr7
array([[2, 3, 4],
[5, 6, 7]])
arr8= np.arange(9).reshape(3,3)
arr8
array([[0,1, 2],
[3, 4, 5],
[6, 7, 8]])
np.dot(arr7,arr8)
array([[33, 42, 51],
[60, 78, 96]])
arr9= np.arange(6).reshape(3,2)
arr9
array([[0,1],
[2, 3],
[4, 5]])
np.dot(arr7,arr9)
array([[22, 31],
[40, 58]])
二维数组与三维数组的运算案例代码如下
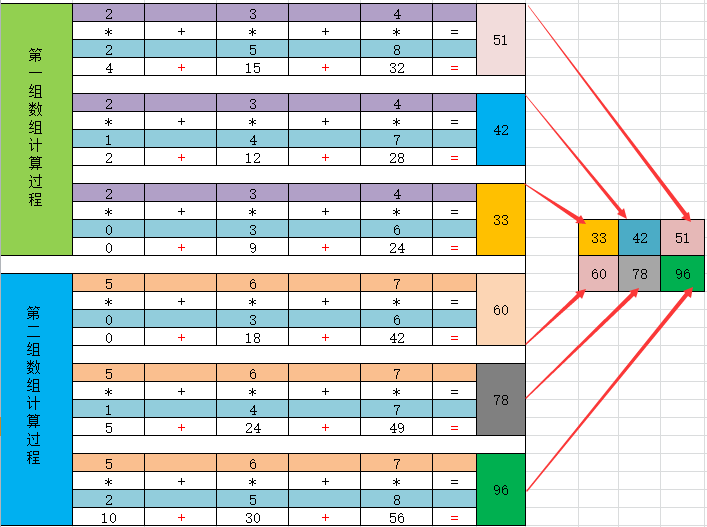
利用表格计算法来解释上面的,二维数组与三维数组的矩阵乘积的结果计算过程如下表4,所示:
表 4
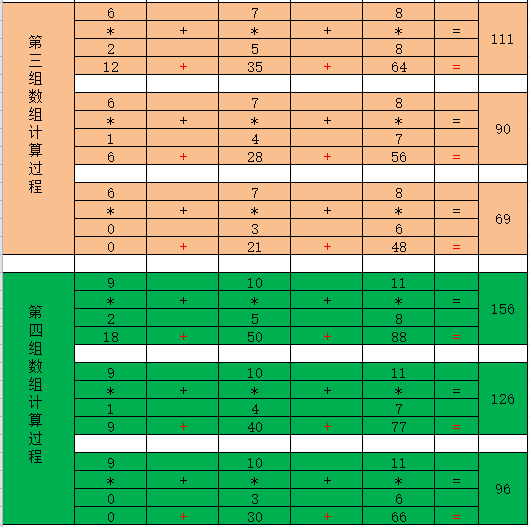
8、如下多维数组的dot函数运算所示:
![]()
![]()
#多维数组的dot函数矩阵运算
arr12 = np.arange(12).reshape(4,3)
arr12
array([[ 0,1, 2],
[3, 4, 5],
[6, 7, 8],
[9, 10, 11]])
arr13= np.arange(9).reshape(3,3)
arr13
array([[0,1, 2],
[3, 4, 5],
[6, 7, 8]])
np.dot(arr12,arr13)
array([[15, 18, 21],
[42, 54, 66],
[69, 90, 111],
[96, 126, 156]])
arr14= np.arange(15).reshape(3,5)
arr14
array([[ 0,1, 2, 3, 4],
[5, 6, 7, 8, 9],
[10, 11, 12, 13, 14]])
np.dot(arr12,arr14)
array([[25, 28, 31, 34, 37],
[70, 82, 94, 106, 118],
[115, 136, 157, 178, 199],
[160, 190, 220, 250, 280]])
多维数组的代码运算如下
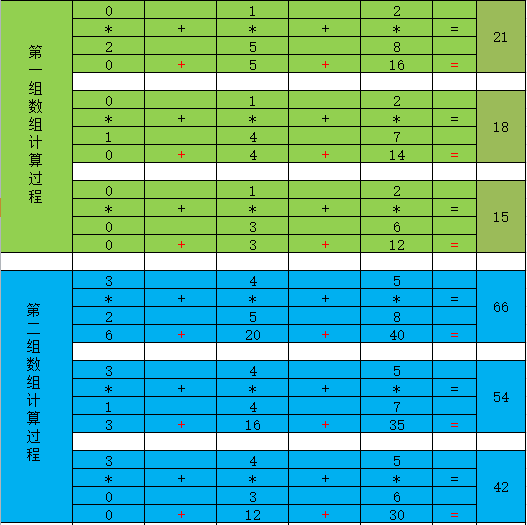
利用表格计算法来解释上面的,多维数组的矩阵乘积的结果计算过程如下表5,表6,表7所示:
表 5 表 6
表 7
9、dot()函数可以通过NumPy库调用,也可以由数组实例对象进行调用。例如:a.dot(b) 与 np.dot(a,b)效果相同。但矩阵积计算不遵循交换律,np.dot(a,b) 和 np.dot(b,a) 得到的结果是不一样的。