常见的数据结构(数组、链表、栈、队列、二叉树)及增删改查的时间复杂度
- 数组(无序数组、有序数组)
- 链表(无序链表、有序链表)
- 栈
- 队列
- 二叉树(有序二叉树:平衡树、红黑树、B类树、非平衡树;无序二叉树:完全数、满树、完美数、哈夫曼树)
- 时间复杂度:
-
数据结构 增 删 改 查 无序数组 O(1) O(n) O(n) O(n) 有序数组 O(n) O(n) O(n) O(logn) 无序链表 O(1) O(n) O(n) O(n) 有序链表 O(n) O(n) O(n) O(n) 栈 O(1) O(1) / / 队列 O(1) O(1) / / 有序树 O(logn) O(logn) O(logn) O(logn)
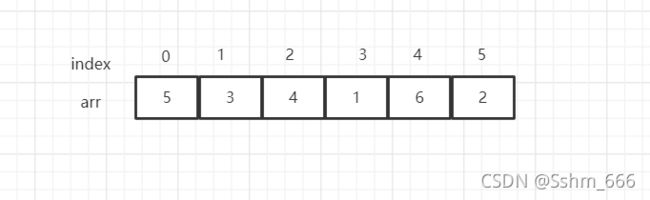
数组:数组是连续的, 通过索引值index查找它的数值arr【index】时直接就可以找到这个值,时间复杂度是O(1)
通过数值查找时它就会从头遍历查找所以它查找的时间复杂度是O(n),
增加操作如果是在最后添加的时间复杂度是O(1),不用查找位置直接添加
删:先查找这个数O(n),删除O(1)后面数往前移O(n),所以是O(n)+o(1)+o(n)=o(n)
改:先查找这个数O(n),改数o(1),所以是O(n)+o(n)=o(n)
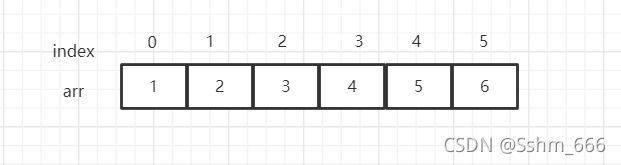
有序数组:如下图,它是连续的但它是有序的,
通过数值查找时它就会由二分法查找所以它查找的时间复杂度是O(logn),
增:需要先找到位置,二分查找o(logn),再把后面的数向后移动o(n),所以是O(logn)+o(n)=o(n)
删:先查找这个数O(logn),删除O(1)后面数往前移O(n),所以是O(logn)+o(1)+o(n)=o(n)
改:有序数组是需要排序的,所以改操作可以认为是先把这个数删除,然后再添加一个改的数, 先查找这个数O(logn),以上增操作时间复杂度是o(n),所以是O(logn)+o(n)=o(n)
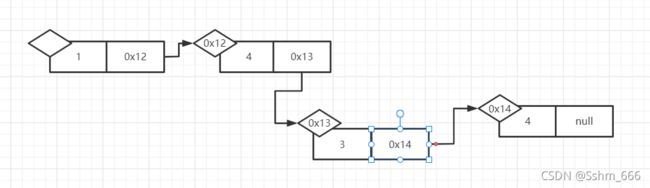
l链表:链表是不连续的,不支持二分查找,它是由数值和指针node两个空间组成的如下图:
无序链表:
查:需要遍历查找时间复杂度o(n)
增:增加一个链,把指针方向和地址改掉就行,所以时间复杂度是0(1)
删:先找到这个值的位置0(n),删除0(1), 时间复杂度是0(1)+0(n)=0(n)
改:先找到这个值的位置0(n),改掉它的值0(1), 时间复杂度是0(1)+0(n)=0(n)
有序链表:
查:需要遍历查找时间复杂度o(n)
增:因为是有序的要排序,需要先找到添加的位置0(n),再增加0(1)所以时间复杂度是0(1)+0(n)=0(n)
删:先找到这个值的位置0(n),删除0(1), 时间复杂度是0(1)+0(n)=0(n)
改:有序链表的改操作认为是先删除这个数O(n)再找到改的这个值的位置o(n),所以时间复杂度是0(n)+0(n)=0(n)
栈:可以把它比作杯子,先进后出,后进先出,操作增添只能在最后一个所以就和对数组的最后一个值操作一样,时间复杂度都是O(1),如下图:
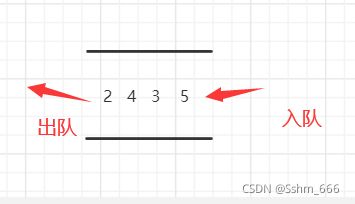
队列:可以把它比作一个管子,先进先出,后进后出,它只能对第一个元素进行删除,最后一个元素进行添加,所以也就是对数组的第一个值进行操作,增删操作时间复杂度也是o(1),如下图:
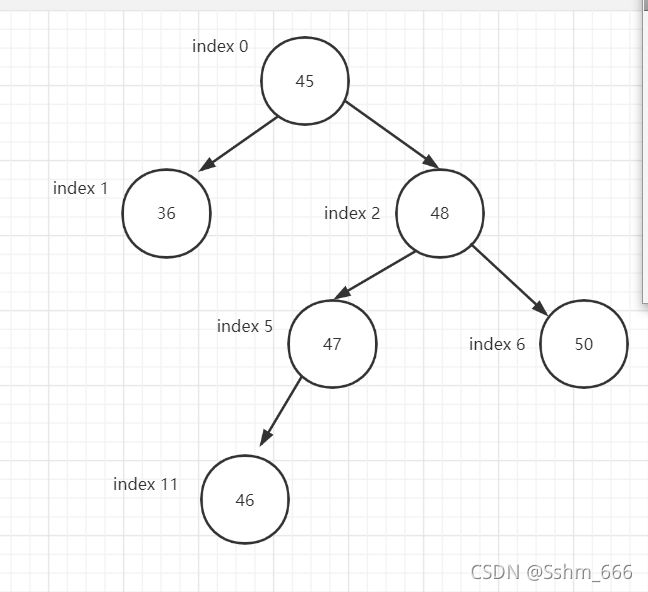
有序二叉树:左子节点比父节点小左子节点是父节点索引值的二倍加一,右子节点比父节点大,右子节点是父节点索引值的二倍加二。如下图:
查:它类似于二分查找,查找时与根节点比较大小,比它大就走右节点反之左节点,由它们之间的索引值关系查找到下一个比较数的位置,所以它的时间复杂度是O(logn)
增:有序树需要先找到它要添加的位置O(logn),直接添加O(1),时间复杂度O(logn)+O(1)=O(logn)
删:先找到位置O(logn),删除O(1),时间复杂度O(logn)+O(1)=O(logn)
改:有序树改操作可以认为是先删这个数再添加这个数,由上所知删时间复杂度O(logn),添加也是O(logn),所以时间复杂度是O(logn)+O(logn)=O(logn)
注意:
- 有序数据结构在处理完依然有序
- 树结构操作快时间复杂度O(logn)
- 有序树删操作会寻找代替点
- 有序树删根节点找左子树的最右节点代替根节点或找右子树的最左节点代替根节点,如果代替点有字树那就让子树代替原位置即可
- 有序树改一个数相当于先删除这个数再添加一个新数
在时间复杂度里O(1)、O(logn)认为是非常快的速度,所以二叉树的数据结构和其他数据结构比较起来是最快的