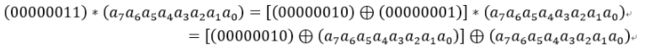（加密基础）AES篇

AES加密

关注微信公众号程序猿与程序媛们，回复，“代码资源”，获取完整的代码实现

AES算法原理和C语言实现

AES加密算法图解

AES算法原理：

AES算法可以归纳为四种操作处理，分别为密钥加法层、字节代换层、行位移层、列混淆层
标准的AES算法密钥和明文都是等长的，一共有128位，196位和256位三种长度，这里重点讲解128位的情况：

128位（16个字节）的的明文会被处理成4X4的二维数组

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16

↓转化

1	5	9	13
2	6	10	14
3	7	11	15
4	8	12	16

，AES算法在处理轮数上只有最后一轮操作与前面的轮数有些不同的地方（少了列混淆这一步），每一轮进行加密时，密钥都会进行一次处理

1.密钥处理

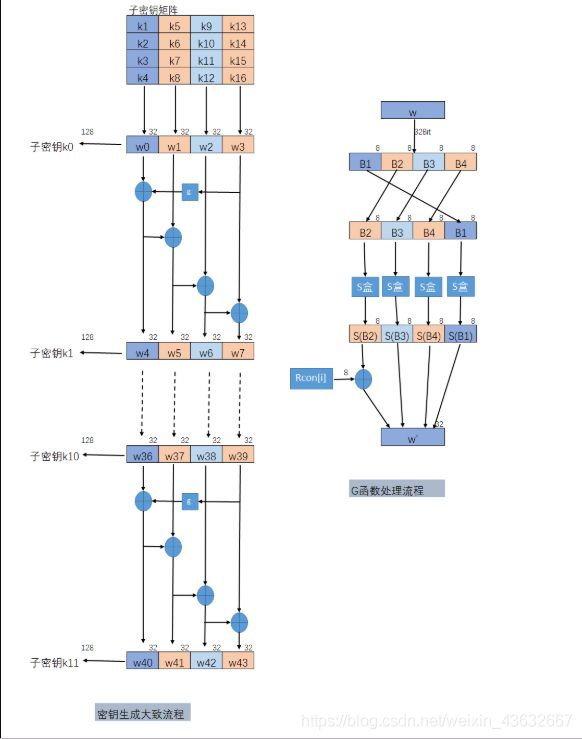
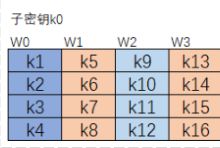
子密钥的生存是以列为单位进行的，子密钥在加密过程中会根据需要生成多个，而这多个密钥都是通过初始密钥扩展而来的

首先将初始密钥（16个字节）转化成4X4的二维数组，然后对该数组进行扩展操作，扩展规则如下：

下图为初始子密钥

我们首先把每一列分成一组分别记为w0,w1,w2,w3,后面依次类推

（1）若w[i]为4的倍数例如w4，那么该列的密钥生成公式如下：

W[i]=W[i-4]^W[i-1]

即将该列往前4个列的每一位和前1个列的进行按位异或操作

（2）若w[i]为4的倍数例如w4，那么该列的密钥生成公式如下：

W[i]=W[i-4]^G(W[i-1])

即将该列往前4个列的每一位和前1个列的G函数返回值进行按位异或操作

G函数首先会将4个输入字节进行翻转，并执行一个按字节的S盒替换，最后用第一个字节与轮系数Rcon进行异或操作。轮系数是一个含有10个元素的一位数组，一个元素1个字节

轮系数Rcon	0x01	0x02	0x04	0x08	0x10	0x20	0x40	0x80	0x1b	0x36

S盒形成过程：S盒是通过将输入的数据进行乘法逆元计算、然后将计算结果进行仿射映射得到的。

具体原理实现稍后补上！！！！

总之按照这种方式，我们最后会生成所有的子密钥
代码如下：

//用于密钥扩展    Rcon[0]作为填充，没有实际用途
const unsigned int Rcon[11] = { 0x00, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1B, 0x36 };
 
 
int Key_S_Substitution(unsigned char(*ExtendKeyArray)[44], unsigned int nCol)
{
    int ret = 0;
 
    for (int i = 0; i < 4; i++)
    {
        ExtendKeyArray[i][nCol] = S_Table[(ExtendKeyArray[i][nCol]) >> 4][(ExtendKeyArray[i][nCol]) & 0x0F];
    }
 
    return ret;
}
 
 
int G_Function(unsigned char(*ExtendKeyArray)[44], unsigned int nCol)
{
    int ret = 0;
 
    //1、将扩展密钥矩阵的nCol-1列复制到nCol列上，并将nCol列第一行的元素移动到最后一行，其他行数上移一行
    for (int i = 0; i < 4; i++)
    {
        ExtendKeyArray[i][nCol] = ExtendKeyArray[(i + 1) % 4][nCol - 1];
    }
 
    //2、将nCol列进行S盒替换
    Key_S_Substitution(ExtendKeyArray, nCol);
 
    //3、将该列第一行元素与Rcon进行异或运算
    ExtendKeyArray[0][nCol] ^= Rcon[nCol / 4];
 
    return ret;
}
 
 
int CalculateExtendKeyArray(const unsigned char(*PasswordArray)[4], unsigned char(*ExtendKeyArray)[44])
{
    int ret = 0;
 
    //1、将密钥数组放入前四列扩展密钥组
    for (int i = 0; i < 16; i++)
    {
        ExtendKeyArray[i & 0x03][i >> 2] = PasswordArray[i & 0x03][i >> 2];
    }
 
    //2、计算扩展矩阵的后四十列
    for (int i = 1; i < 11; i++)    //进行十轮循环
    {
        //(1)如果列号是4的倍数，这执行G函数  否则将nCol-1列复制到nCol列上
        G_Function(ExtendKeyArray, 4*i);
 
        //(2)每一轮中，各列进行异或运算
        //      列号是4的倍数
        for (int k = 0; k < 4; k++)//行号
        {
            ExtendKeyArray[k][4 * i] = ExtendKeyArray[k][4 * i] ^ ExtendKeyArray[k][4 * (i - 1)];
        }
 
        //      其他三列
        for (int j = 1; j < 4; j++)//每一轮的列号
        {
            for (int k = 0; k < 4; k++)//行号
            {
                ExtendKeyArray[k][4 * i + j] = ExtendKeyArray[k][4 * i + j - 1] ^ ExtendKeyArray[k][4 * (i - 1) + j];
            }
        }
    }
 
    return ret;
}

1.明文加密之字节代换层

字节代换层的主要功能是让数据通过S盒完成从一个字节到另一个字节的映射，S盒的计算方式和密钥中S盒计算方式相同。S盒是一个拥有256个字节元素的数组，逆S盒与S盒对应用于AES算法的解密，字节代换层将明文的每一个字节作为数组下标，对进行相关索引操作

若将S盒作为一维数组处理，则只需要将每个字节作为索引下标进行索引

若将S盒作为二维数组，则需要将每个字节的高4位作为第一个下标，第四位作为第二个下标来进行索引

S_box[高四位][低四位]

代码实现如下：

//S盒
const unsigned char S_Table[16][16] =
{
    0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76,
    0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0,
    0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15,
    0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75,
    0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84,
    0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF,
    0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8,
    0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2,
    0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73,
    0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB,
    0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79,
    0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08,
    0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A,
    0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E,
    0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF,
    0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16
};
 
//字节代换
int Plain_S_Substitution(unsigned char *PlainArray)
{
    int ret = 0;
 
    for (int i = 0; i < 16; i++)
    {
        PlainArray[i] = S_Table[PlainArray[i] >> 4][PlainArray[i] & 0x0F];
    }
 
    return ret;
}
 
 
//逆S盒
const unsigned char ReS_Table[16][16] =
{
    0x52, 0x09, 0x6A, 0xD5, 0x30, 0x36, 0xA5, 0x38, 0xBF, 0x40, 0xA3, 0x9E, 0x81, 0xF3, 0xD7, 0xFB,
    0x7C, 0xE3, 0x39, 0x82, 0x9B, 0x2F, 0xFF, 0x87, 0x34, 0x8E, 0x43, 0x44, 0xC4, 0xDE, 0xE9, 0xCB,
    0x54, 0x7B, 0x94, 0x32, 0xA6, 0xC2, 0x23, 0x3D, 0xEE, 0x4C, 0x95, 0x0B, 0x42, 0xFA, 0xC3, 0x4E,
    0x08, 0x2E, 0xA1, 0x66, 0x28, 0xD9, 0x24, 0xB2, 0x76, 0x5B, 0xA2, 0x49, 0x6D, 0x8B, 0xD1, 0x25,
    0x72, 0xF8, 0xF6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xD4, 0xA4, 0x5C, 0xCC, 0x5D, 0x65, 0xB6, 0x92,
    0x6C, 0x70, 0x48, 0x50, 0xFD, 0xED, 0xB9, 0xDA, 0x5E, 0x15, 0x46, 0x57, 0xA7, 0x8D, 0x9D, 0x84,
    0x90, 0xD8, 0xAB, 0x00, 0x8C, 0xBC, 0xD3, 0x0A, 0xF7, 0xE4, 0x58, 0x05, 0xB8, 0xB3, 0x45, 0x06,
    0xD0, 0x2C, 0x1E, 0x8F, 0xCA, 0x3F, 0x0F, 0x02, 0xC1, 0xAF, 0xBD, 0x03, 0x01, 0x13, 0x8A, 0x6B,
    0x3A, 0x91, 0x11, 0x41, 0x4F, 0x67, 0xDC, 0xEA, 0x97, 0xF2, 0xCF, 0xCE, 0xF0, 0xB4, 0xE6, 0x73,
    0x96, 0xAC, 0x74, 0x22, 0xE7, 0xAD, 0x35, 0x85, 0xE2, 0xF9, 0x37, 0xE8, 0x1C, 0x75, 0xDF, 0x6E,
    0x47, 0xF1, 0x1A, 0x71, 0x1D, 0x29, 0xC5, 0x89, 0x6F, 0xB7, 0x62, 0x0E, 0xAA, 0x18, 0xBE, 0x1B,
    0xFC, 0x56, 0x3E, 0x4B, 0xC6, 0xD2, 0x79, 0x20, 0x9A, 0xDB, 0xC0, 0xFE, 0x78, 0xCD, 0x5A, 0xF4,
    0x1F, 0xDD, 0xA8, 0x33, 0x88, 0x07, 0xC7, 0x31, 0xB1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xEC, 0x5F,
    0x60, 0x51, 0x7F, 0xA9, 0x19, 0xB5, 0x4A, 0x0D, 0x2D, 0xE5, 0x7A, 0x9F, 0x93, 0xC9, 0x9C, 0xEF,
    0xA0, 0xE0, 0x3B, 0x4D, 0xAE, 0x2A, 0xF5, 0xB0, 0xC8, 0xEB, 0xBB, 0x3C, 0x83, 0x53, 0x99, 0x61,
    0x17, 0x2B, 0x04, 0x7E, 0xBA, 0x77, 0xD6, 0x26, 0xE1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0C, 0x7D
};
//逆字节代换
int Cipher_S_Substitution(unsigned char *CipherArray)
{
    int ret = 0;
 
    for (int i = 0; i < 16; i++)
    {
        CipherArray[i] = ReS_Table[CipherArray[i] >> 4][CipherArray[i] & 0x0F];
    }
 
    return ret;
}

2.明文加密之行位移

行位移的操作是将数据作为一个4X4的字节矩阵处理，然后将这个矩阵的字节进行位置上的置换，其位移操作非常简单：

将第一行保持不变，第二行整体向左移1个字节，第三行整体向左位移2个字节，第四行整体左移3个字节

int ShiftRows(unsigned int *PlainArray)
{
    int ret = 0;
 
    //第一行 不移位
    //PlainArray[0] = PlainArray[0];
 
    //第二行 左移8Bit
    PlainArray[1] = (PlainArray[1] >> 8) | (PlainArray[1] << 24);
 
    //第三行 左移16Bit
    PlainArray[2] = (PlainArray[2] >> 16) | (PlainArray[2] << 16);
 
    //第四行 左移24Bit
    PlainArray[3] = (PlainArray[3] >> 24) | (PlainArray[3] << 8);
 
    return ret;
}

2.明文加密之列混淆

列混淆负责对AES算法的元素进行扩散操作，其中包含了矩阵乘法、伽罗瓦域加法和乘法操作

经过了行位移操作后的矩阵通过和固定矩阵相乘得到混淆后的矩阵

而根据伽罗瓦域的相关加法和乘法性质，由于两个矩阵的加法和乘法都在GF(2^8)中进行，而在扩展域中加法操作等同于异或操作，乘法操作需要通过一个乘法函数实现

伽罗瓦域相关知识：矩阵元素的乘法和加法都是定义在基于GF(2^8)上的二元运算,并不是通常意义上的乘法和加法，

其实这种二元运算的加法等价于两个字节的异或

乘法则复杂一点。对于一个8位的二进制数来说，使用域上的乘法乘以(00000010)等价于左移1位(低位补0)后，再根据情况同(00011011)进行异或运算

举个栗子：
假设S1=（a7,a6,a5,a4,a3,a2,a1,a0）,那么0x02*S1，就可以理解为

即，如果a7=1，则进行异或操作，否则就不进行任何操作

同理，若为S1*（00000100）那么就将（00000100）拆分成两个（00000010）进行乘法操作

若为S1*（00000011）那么久按照如下拆分,将两个乘积分别异或

伽罗瓦域乘法：

///
//功能:   伽罗瓦域内的乘法运算  GF(128)
//参数:   Num_L           输入的左参数
//      Num_R           输入的右参数
//返回值:计算结果
char GaloisMultiplication(unsigned char Num_L, unsigned char Num_R)
{
    //定义变量
    unsigned char Result = 0;       //伽罗瓦域内乘法计算的结果
 
    while (Num_L)
    {
        //如果Num_L最低位是1就异或Num_R，相当于加上Num_R * 1
        if (Num_L & 0x01)
        {
            Result ^= Num_R;
        }
 
        //Num_L右移一位，相当于除以2
        Num_L = Num_L >> 1;
 
        //如果Num_R最高位为1
        if (Num_R & 0x80)
        {
            //左移一位相当于乘二
            Num_R = Num_R << 1;     //注：这里会丢失最高位，但是不用担心
 
            Num_R ^= 0x1B;  //计算伽罗瓦域内除法Num_R = Num_R / (x^8(刚好丢失最高位) + x^4 + x^3 + x^1 + 1)
        }
        else
        {
            //左移一位相当于乘二
            Num_R = Num_R << 1;
        }
    }
    return Result;
}

矩阵乘法：

//列混淆左乘矩阵
const unsigned char MixArray[4][4] =
{
    0x02, 0x03, 0x01, 0x01,
    0x01, 0x02, 0x03, 0x01,
    0x01, 0x01, 0x02, 0x03,
    0x03, 0x01, 0x01, 0x02
};
 
int MixColum(unsigned char(*PlainArray)[4])
{
    int ret = 0;
    //定义变量
    unsigned char ArrayTemp[4][4];
 
    //初始化变量
    memcpy(ArrayTemp, PlainArray, 16);
 
    //矩阵乘法 4*4
    for (int i = 0; i < 4; i++)
    {
        for (int j = 0; j < 4; j++)
        {
            PlainArray[i][j] =
                MixArray[i][0] * ArrayTemp[0][j] +
                MixArray[i][1] * ArrayTemp[1][j] +
                MixArray[i][2] * ArrayTemp[2][j] +
                MixArray[i][3] * ArrayTemp[3][j];
        }
    }
 
    return ret;
}

整体列混淆代码：

const unsigned char MixArray[4][4] =
{
    0x02, 0x03, 0x01, 0x01,
    0x01, 0x02, 0x03, 0x01,
    0x01, 0x01, 0x02, 0x03,
    0x03, 0x01, 0x01, 0x02
};
 
int MixColum(unsigned char(*PlainArray)[4])
{
    int ret = 0;
    //定义变量
    unsigned char ArrayTemp[4][4];
 
    //初始化变量
    memcpy(ArrayTemp, PlainArray, 16);
 
    //矩阵乘法 4*4
    for (int i = 0; i < 4; i++)
    {
        for (int j = 0; j < 4; j++)
        {
            PlainArray[i][j] =
                GaloisMultiplication(MixArray[i][0], ArrayTemp[0][j]) ^
                GaloisMultiplication(MixArray[i][1], ArrayTemp[1][j]) ^
                GaloisMultiplication(MixArray[i][2], ArrayTemp[2][j]) ^
                GaloisMultiplication(MixArray[i][3], ArrayTemp[3][j]);
        }
    }
    return ret;
}

Java代码实现

import java.util.Base64;
import java.security.Key;
import javax.crypto.Cipher;
import javax.crypto.KeyGenerator;
import javax.crypto.SecretKey;
import javax.crypto.spec.SecretKeySpec;
public class AES {
public static final String KEY_ALGORITHM="AES";
public static final String CIPHER_ALGORITHM="AES/ECB/PKCS5Padding";
private static Key toKey(byte[] key) throws Exception{
	//实例化AES密钥
	SecretKey secretKey=new SecretKeySpec(key,KEY_ALGORITHM);
	return secretKey;
	}
public static byte[] decrypt(byte[] data,byte[] key)throws Exception{
	Key k=toKey(key);
	Cipher cipher =Cipher.getInstance(CIPHER_ALGORITHM);
	cipher.init(Cipher.DECRYPT_MODE, k);
	return cipher.doFinal(data);
	}
public static byte[] encrypt(byte[] data,byte[] key)throws Exception{
	Key k=toKey(key);
	Cipher cipher=Cipher.getInstance(CIPHER_ALGORITHM);
	cipher.init(Cipher.ENCRYPT_MODE, k);
	return cipher.doFinal(data);
}
public static byte[] initKey() throws Exception{
	//实例化
	KeyGenerator kg=KeyGenerator.getInstance(KEY_ALGORITHM);
	//AES 要求密钥长度为128位，192位或者256位
	kg.init(128);
	//生成密钥
	SecretKey secretKey=kg.generateKey();
	//获得密钥的二进制编码形式
	return secretKey.getEncoded();
}
public static void main(String[] args) throws Exception {
	String inputStr="AES";
	byte[] inputData=inputStr.getBytes();
	System.out.println("原文：\t"+inputStr);
	byte[] key=AES.initKey();
	System.out.println("密钥：\t"+new String(Base64.getEncoder().encode(key)));
	//加密
	inputData=AES.encrypt(inputData, key);
	System.out.println("加密后：\t"+new String(Base64.getEncoder().encode(inputData)));
	byte[] outputData=AES.decrypt(inputData, key);
	String outputStr=new String(outputData);
	System.out.println("解密后：\t"+outputStr);
//S2Tpe4l3YKuJB8Ew51dAprqX2WKJhRUxM5SolIgqnoY=
//KK7tt4PIdJZkTwz6t0d2at6eEkifcTtsoSHl2J1BmD8=
}
}

参考链接：
https://blog.csdn.net/qq_28205153/article/details/55798628
https://bbs.pediy.com/thread-253884.htm