代码随想录算法训练营第46天 | 139.单词拆分 多重背包的理论 背包的小总结
代码随想录系列文章目录
动态规划篇 —— 切割子串问题 + 背包收尾
文章目录
- 代码随想录系列文章目录
- 139.单词拆分(切割问题)
-
- dfs写法
- dp解法
- 多重背包的理论基础(展开成01背包)
- 背包问题小总结篇
-
- 最近做的一些背包问题的具体变式,在这里也做个总结
- 遍历顺序
139.单词拆分(切割问题)
题目链接
这道题也是刚开始刷题的时候就做过,可以用经典的dfs + 记搜 过掉
dfs写法
def wordBreak(self, s: str, wordDict: List[str]) -> bool:
self.mem = [-1] * (len(s)+1)
def back_track(idx):
if idx == len(s):
return True
if self.mem[idx] != -1:
return self.mem[idx]
res = False
for i in range(idx, len(s) + 1):
if s[idx:i+1] in wordDict and back_track(i+1):
res = True
self.mem[idx] = res
return res
return back_track(0)
当然,我喜欢直接@fuctools.lru_cache()去清空栈
class Solution:
def wordBreak(self, s: str, wordDict: List[str]) -> bool:
import functools
@functools.lru_cache(None)
def rec(start):
if start >= len(s):
if start == len(s):
return True
return
res = False
for i in range(start, len(s)+1):
if s[start:i+1] in wordDict and rec(i+1):
res = True
return res
return rec(0)
这道题和之前刷过的回溯篇的切割问题十分相似,131.分割回文串131分割回文子串,93.复原IP地址93复原ip地址
dfs的过程基本一致,我觉得可以放在一起做一个总结
dp解法
如何把思路转化到dp, 我们可以想到,单词就是物品,字符串s就是背包,单词能否组成字符串s,就是问物品能不能把背包装满
拆分时可以重复使用字典中的单词,说明就是一个完全背包!
按照这个思路我们去做dp的分析
1.状态定义:
dp[j] 表示 字符串长度为j的话,dp[j]为true,表示可以拆分为一个或多个在字典中出现的单词
2.状态转移:
那么dp[j] 如何推导过来呢,我们看上一个状态, dp[i],如果dp[i]是True, 并且s[i:j]在字典里,那么说明dp[j]也是True
3.base case
从递归公式中可以看出,dp[j] 的状态依靠 dp[i]是否为true,那么dp[0]就是递归的根基,dp[0]一定要为true,否则递归下去后面都都是false了。
其余的初始化为False
4.遍历顺序以及解的所在
这道题不涉及排列,所以我习惯先遍历物品再遍历背包,完全背包都是正序
但本题还有特殊性,因为是要求子串,最好是遍历背包放在外循环,将遍历物品放在内循环。
如果要是外层for循环遍历物品,内层for遍历背包,就需要把所有的子串都预先放在一个容器里。
def wordBreak(self, s: str, wordDict: List[str]) -> bool:
dp = [False] * (len(s)+1)
dp[0] = True
for j in range(1,len(s)+1):
for i in range(0,j):
if dp[i] and s[i:j] in wordDict:
dp[j] = True
return dp[len(s)]
这个我需要解释一下为什么 切片是s[i:j], 你要明白我们的j的范围其实是dp数组的范围,我们dp数组多开了一位放dp[0], 所以j天然就比字符串s偏后一位 切片依然是左闭右开的
多重背包的理论基础(展开成01背包)
首先明白多重背包问题指的是什么情景
01背包,每种物品只有一个,选和不选
完全背包, 每种物品有无限多个,选和不选,选多少跟遍历顺序有关
多重背包是建立在01背包基础上的,不同物品数量不同,选和不选,选多少
每件物品最多有ki件可用,把ki件摊开,其实就是一个01背包问题了。
这个摊开有两种方式,第一种是在遍历物品正序,遍历容积反序,的基础上
增加第三层遍历,选和不选,选几个
def test_multi_pack1():
'''版本:改变遍历个数'''
weight = [1, 3, 4]
value = [15, 20, 30]
nums = [2, 3, 2]
bag_weight = 10
dp = [0] * (bag_weight + 1)
for i in range(len(weight)):
for j in range(bag_weight, weight[i] - 1, -1):
# 以上是01背包,加上遍历个数
for k in range(1, nums[i] + 1):
if j - k * weight[i] >= 0:
dp[j] = max(dp[j], dp[j - k * weight[i]] + k * value[i])
print(" ".join(map(str, dp)))
if __name__ == '__main__':
test_multi_pack1()
第二种是直接把每种物品有几个加在weight和value数组里,直接扩容数组 然后就变成01背包了
def test_multi_pack2():
'''改变物品数量为01背包格式'''
weight = [1, 3, 4]
value = [15, 20, 30]
nums = [2, 3, 2]
bag_weight = 10
for i in range(len(nums)):
# 将物品展开数量为1
while nums[i] > 1:
weight.append(weight[i])
value.append(value[i])
nums[i] -= 1
dp = [0] * (bag_weight + 1)
# 遍历物品
for i in range(len(weight)):
# 遍历背包
for j in range(bag_weight, weight[i] - 1, -1):
dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
print(" ".join(map(str, dp)))
if __name__ == '__main__':
test_multi_pack2()
这两种情况的时间复杂度是一样的
时间复杂度:O(m × n × k),m:物品种类个数,n背包容量,k单类物品数量
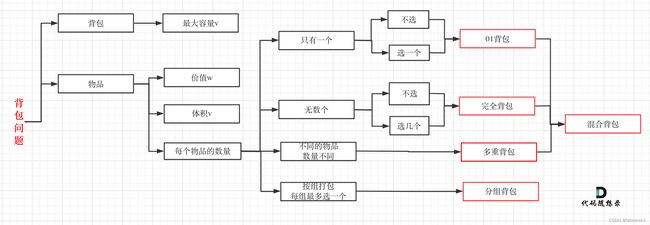
背包问题小总结篇
最近做的一些背包问题的具体变式,在这里也做个总结
问能否能装满背包(或者最多装多少):dp[j] = max(dp[j], dp[j - nums[i]] + nums[i])
对应如下题目:
416.分割等和子集
1049. 最后一块石头的重量 II
问装满背包有几种方法:dp[j] += dp[j - nums[i]] ,对应题目如下
494.目标和
518. 零钱兑换 II
377. 组合总和 Ⅳ
爬楼梯完全背包版本
组合的话 外层遍历物品,内层遍历背包,如果是完全背包的话内层正序
排列的话 外层遍历背包 , 内层遍历物品,如果是完全背包的话都是正序
问背包装满最大价值:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); ,对应题目如下:
474.一和零
问装满背包所有物品的最小个数:dp[j] = min(dp[j - coins[i]] + 1, dp[j]); ,对应题目如下:
322.零钱兑换
279.完全平方数
遍历顺序
01背包:
二维dp数组01背包先遍历物品还是先遍历背包都是可以的,且第二层for循环是从小到大遍历。
一维dp数组01背包只能先遍历物品再遍历背包容量,且第二层for循环是从大到小遍历。
(从大到小是为了一个物品只能选一次,避免重复)
完全背包:
纯完全背包的一维dp数组实现,先遍历物品还是先遍历背包都是可以的,且第二层for循环是从小到大遍历。
但是仅仅是纯完全背包的遍历顺序是这样的,题目稍有变化,两个for循环的先后顺序就不一样了。
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
相关题目如下:
求组合数:518. 零钱兑换 II
求排列数:
377. 组合总和 Ⅳ
爬楼梯完全背包版本
如果求最小数,那么两层for循环的先后顺序就无所谓了,相关题目如下:
322.零钱兑换
279.完全平方数
对于背包问题,其实递推公式算是容易的,难是难在遍历顺序上,如果把遍历顺序搞透,才算是真正理解了。