优化问题-LP，QP和QCQP（线性规划，Linear Programming； 二次规划，Quadratic Programming；二次约束二次规划）

线性规划（LP）

LP问题的一般形式为：
$$\begin{array}{ll}\min & {\mathbf{c}}^T\mathbf{x}\\ \text{ s.t. }& \mathbf{G}\mathbf{x}⪯\mathbf{h}\end{array}（6.1）$$
本质：LP问题即是在多面体上找到一个可行解使得线性目标函数最小。

LP的一般形式可以转化为标准形式，即引入松弛变量：
$$\mathbf{s}\triangleq \mathbf{h}-\mathbf{G}\mathbf{x}$$
作为助变量。则（6.1）可以表示为：
$$\begin{array}{ll}\min & {\mathbf{c}}^T\mathbf{x}\\ \text{ s.t. }& \mathbf{s}⪰0,\mathbf{h}-\mathbf{G}\mathbf{x}=\mathbf{s}\end{array}（6.2）$$
进一步：$\mathrm{x}={\mathrm{x}}_{+}-{\mathrm{x}}_{-}$，其中${\mathrm{x}}_{+},{\mathrm{x}}_{-}⪰0$，则（6.2）可以等价为：
$$\begin{array}{ll}\min & \left[\begin{array}{lll}{\mathbf{c}}^T& -{\mathbf{c}}^T& 0^T\end{array}\right]\left[\begin{array}{c}{\mathbf{x}}_{+}\\ {\mathbf{x}}_{-}\\ \mathbf{s}\end{array}\right]\\ \text{ s.t. }& \left[\begin{array}{c}{\mathrm{x}}_{+}\\ {\mathrm{x}}_{-}\\ \mathrm{s}\end{array}\right]⪰0,\left[\begin{array}{lll}\mathbf{G}& -\mathbf{G}& \mathbf{I}\end{array}\right]\left[\begin{array}{c}{\mathrm{x}}_{+}\\ {\mathrm{x}}_{-}\\ \mathrm{s}\end{array}\right]=\mathrm{h}\end{array}（6.3）$$
（6.3）可以重新表示为标准LP形式：
$$\begin{array}{ll}\min & {\mathbf{c}}^T\mathbf{x}\\ \text{ s.t. }& \mathbf{x}⪰0,\mathbf{A}\mathbf{x}=\mathbf{b}\end{array}$$
其中
$$\mathbf{A}=\left[\begin{array}{lll}\mathbf{G}& -\mathbf{G}& \mathbf{I}\end{array}\right],c={\left[{\mathbf{c}}^T-{\mathbf{c}}^T{0}^T\right]}^T,x={\left[{\mathbf{x}}_{+}^T{\mathbf{x}}_{-}^T{\mathbf{s}}^T\right]}^T$$
其中$\mathbf{x}$是未知变量。

LP的一些例子：

Chebyshev中心

考虑欧式球$B\left({\mathbf{x}}_c,r\right)=\left\{\mathbf{x}\mid {\Vert \mathbf{x}-{\mathbf{x}}_c\Vert }_2\le r\right\}$以及多面体$\mathcal{P}=\{\mathbf{x}\mid {\mathbf{a}}_i^T\mathbf{x}\le b_i,i=1,\dots ,m\}$

Chebyshev问题描述为，在多面体$\mathcal{P}$中找到最大的欧式球，如下图所示。该问题表示为：

$$\begin{array}{rl}{\max }_{{\mathbf{x}}_c,r}& r\\ \text{ s.t. }& B\left({\mathbf{x}}_c,r\right)\subseteq \mathcal{P}=\left\{\mathbf{x}\mid {\mathbf{a}}_i^T\mathbf{x}\le b_i,i=1,\dots ,m\right\}\end{array}（6.6）$$
该问题看起来是非凸的，但可以转化为LP。考虑欧式球的另一种定义：
$$B\left({\mathbf{x}}_c,r\right)=\left\{{\mathbf{x}}_c+\mathbf{u}\mid \Vert \mathbf{u}{\Vert }_2\le r\right\}$$

考虑Cauchy-Schwartz inequality：有：
$${\mathbf{a}}_i^T\mathbf{u}\le {\Vert {\mathbf{a}}_i\Vert }_2\cdot \Vert \mathbf{u}{\Vert }_2$$
考虑（6.6）的约束集可以重新表示为：
$$\begin{array}{rl}B\left({\mathrm{x}}_c,r\right)\subseteq \mathcal{P}& ⟺\sup \left\{{\mathbf{a}}_i^T\left({\mathrm{x}}_c+\mathbf{u}\right)\mid \Vert \mathbf{u}{\Vert }_2\le r\right\}\le b_i,\forall i\\ & ⟺{\mathbf{a}}_i^T{\mathbf{x}}_c+r{\Vert {\mathbf{a}}_i\Vert }_2\le b_i,\forall i\text{ (i.e., }\mathbf{u}=r\frac{{\mathbf{a}}_i}{{\Vert {\mathbf{a}}_i\Vert }_2}),\end{array}$$
因此Chebyshev 中心问题可以表示为：
$$\begin{array}{rl}{\max }_{{\mathbf{x}}_c,r}& r\\ \text{ s.t. }& {\mathbf{a}}_i^T{\mathbf{x}}_c+r{\Vert {\mathbf{a}}_i\Vert }_2\le b_i,i=1,\dots ,m.\end{array}$$

${\ell }_{\infty }$-norm 近似问题：

${\ell }_{\infty }$-norm 定义为：
$$\min \Vert \mathrm{A}\mathrm{x}-\mathrm{b}{\Vert }_{\infty }$$
其中：$\mathbf{A}\in {\mathbb{R}}^{m\times n}$和$\mathbf{b}\in {\mathbb{R}}^m$。利用epigraph形式有：
$$\begin{array}{rl}& \min t\\ & \begin{array}{l}\text{ s.t. }{\max }_{i=1,\dots ,m}\left|r_i\right|\le t\\ \mathbf{r}=\mathbf{A}\mathbf{x}-\mathbf{b}\end{array}\end{array}$$
进一步有：
$$\begin{array}{l}\min t\\ \text{ s.t. }-t{1}_m⪯\mathbf{r}⪯t{1}_m\\ \mathbf{r}=\mathbf{A}\mathbf{x}-\mathbf{b}\end{array}$$
这是一个LP问题，$\mathbf{r}$是新定义的辅助变量。$\mathbf{x}$、$\mathbf{r}$和$t$均为未知变量。

${\ell }_1$-norm 近似问题：

$$\min \Vert \mathbf{A}\mathbf{x}-\mathbf{b}{\Vert }_1$$
其中：$\mathbf{A}\in {\mathbb{R}}^{m\times n}$和$\mathbf{b}\in {\mathbb{R}}^m$。同样可以转化为LP问题：
$$\begin{array}{l}\min {\sum }_{i=1}^m\left|r_i\right|\\ \text{ s.t. }\mathbf{r}=\mathbf{A}\mathbf{x}-\mathbf{b}\end{array}$$
进一步有：
$$\begin{array}{rl}\min & \sum _{i=1}^m{t}_i\\ \text{ s.t. }& -t_i\le r_i\le t_i,i=1,\dots ,m\\ & \mathbf{r}=\mathbf{A}\mathbf{x}-\mathbf{b}\end{array}$$
这是一个LP问题，$\mathbf{r}$是新定义的辅助变量。$\mathbf{x}$、$\mathbf{r}$和$t_i$，$i=1,...,m$ 均为未知变量。

二次规划（QP）

二次规划形式如下：
$$\begin{array}{rl}\min & \frac{1}{2}{\mathbf{x}}^T\mathbf{P}\mathbf{x}+{\mathbf{q}}^T\mathbf{x}+r\\ \text{ s.t. }& \mathbf{A}\mathbf{x}=\mathbf{b},\mathbf{G}\mathbf{x}⪯\mathbf{h}\end{array}$$
其中$\mathbf{P}\in {\mathbb{S}}^n$, $\mathbf{G}\in {\mathbb{R}}^{m\times n}$和$\mathbf{A}\in {\mathbb{R}}^{p\times n}$。当且仅当$\mathbf{P}⪰0$时QP问题是凸问题

本质：QP问题即是在多面体上找到一个可行解使得二次目标函数最小。

QP的例子：

有界约束最小二乘问题

$$\begin{array}{c}\min \Vert \mathbf{A}\mathbf{x}-\mathbf{b}{\Vert }_2^2\\ \text{ s.t. }\ell ⪯\mathbf{x}⪯\mathbf{u}\end{array}$$
由于$\Vert \mathbf{A}\mathbf{x}-\mathbf{b}{\Vert }_2^2={\mathbf{x}}^T\left({\mathbf{A}}^T\mathbf{A}\right)\mathbf{x}-2{\mathbf{b}}^T\mathbf{A}\mathbf{x}+{\mathbf{b}}^T\mathbf{b}$。因此，是一个QP问题。

多面体的距离

$$\begin{array}{rl}\min & {\Vert {\mathbf{x}}_1-{\mathbf{x}}_2\Vert }_2^2\\ \text{ s.t. }& {\mathbf{A}}_1{\mathbf{x}}_1⪯{\mathbf{b}}_1,{\mathbf{A}}_2{\mathbf{x}}_2⪯{\mathbf{b}}_2\end{array}$$
其中，${\mathbf{x}}_1\in {\mathbb{R}}^n$和${\mathrm{x}}_2\in {\mathbb{R}}^n$。令$\mathbf{x}={\left[{\mathbf{x}}_1^T,{\mathbf{x}}_2^T\right]}^T\in {\mathbb{R}}^{2n}$，然后有：
$$\begin{array}{l}\min {\Vert \left[{\mathbf{I}}_n,-{\mathbf{I}}_n\right]\mathbf{x}\Vert }_2^2\\ \text{ s.t. }\left[\begin{array}{cc}{\mathbf{A}}_1& 0\\ 0& {\mathbf{A}}_2\end{array}\right]\mathbf{x}⪯\left[\begin{array}{l}{\mathbf{b}}_1\\ {\mathbf{b}}_2\end{array}\right]\end{array}$$
该问题是一个QP问题，因为$${\Vert \left[{\mathbf{I}}_n,-{\mathbf{I}}_n\right]\mathbf{x}\Vert }_2^2={\mathbf{x}}^T\left[\begin{array}{cc}{\mathbf{I}}_n& -{\mathbf{I}}_n\\ -{\mathbf{I}}_n& {\mathbf{I}}_n\end{array}\right]\mathbf{x}$$

二次约束二次规划（QCQP）

一般形式如下：
$$\begin{array}{ll}\min & \frac{1}{2}{\mathbf{x}}^T{\mathbf{P}}_0\mathbf{x}+{\mathbf{q}}_0^T\mathbf{x}+r_0\\ \text{ s.t. }& \frac{1}{2}{\mathbf{x}}^T{\mathbf{P}}_i\mathbf{x}+{\mathbf{q}}_i^T\mathbf{x}+r_i\le 0,i=1,\dots ,m\\ & \mathbf{A}\mathbf{x}=\mathbf{b}\end{array}（6.108）$$
其中，${\mathbf{P}}_i\in {\mathbb{S}}^n,i=0,1,\dots ,m$和$\mathbf{A}\in {\mathbb{R}}^{p\times n}$。

QCQP的一些特殊情况和特点：

• 如果${\mathbf{P}}_i⪰0$，$\forall i$，则QCQP是凸的。
• 当${\mathbf{P}}_i\succ 0$，$i=1,...,m$，则QCQP是$m$个椭球交集上的二次最小化问题，且仿射集为$\{\mathbf{x}\mid \mathbf{A}\mathbf{x}=\mathbf{b}\}$
• 如果${\mathbf{P}}_i=0$，$i=1,...,m$，则QCQP退化为QP。
• 如果${\mathbf{P}}_i=0$，$i=0,1,...,m$，则QCQP退化为LP。
• 对于$\forall i=0,...,m$，因为
  $$\frac{1}{2}{\mathbf{x}}^T{\mathbf{P}}_i\mathbf{x}+{\mathbf{q}}_i^T\mathbf{x}+r_i={\Vert {\mathbf{A}}_i\mathbf{x}+{\mathbf{b}}_i\Vert }_2^2-{\left({\mathbf{f}}_i^T\mathbf{x}+d_i\right)}^2$$
  对于问题定义域内的任意$\mathbf{x}$有${\mathbf{f}}_0=0_n$且${\mathbf{f}}_i^T\mathbf{x}+d_i>0$，则（6.108）等价于
  $$\begin{array}{rl}\min & {\Vert {\mathbf{A}}_0\mathbf{x}+{\mathbf{b}}_0\Vert }_2\\ \text{ s.t. }& {\Vert {\mathbf{A}}_i\mathbf{x}+{\mathbf{b}}_i\Vert }_2\le {\mathbf{f}}_i^T\mathbf{x}+d_i,i=1,\dots ,m\\ & \mathbf{A}\mathbf{x}=\mathbf{b}\end{array}$$
  或者考虑epigraph形式有：
  $$\begin{array}{rl}\min & t\\ \text{ s.t. }& {\Vert {\mathbf{A}}_0\mathbf{x}+{\mathbf{b}}_0\Vert }_2\le t\\ & {\Vert {\mathbf{A}}_i\mathrm{x}+{\mathbf{b}}_i\Vert }_2\le {\mathbf{f}}_i^T\mathbf{x}+d_i,i=1,\dots ,m\\ & \mathbf{A}\mathbf{x}=\mathbf{b}\end{array}$$
  这也是一个SOCP（二阶锥规划）问题

QP和QCQP在beamforming设计中的应用

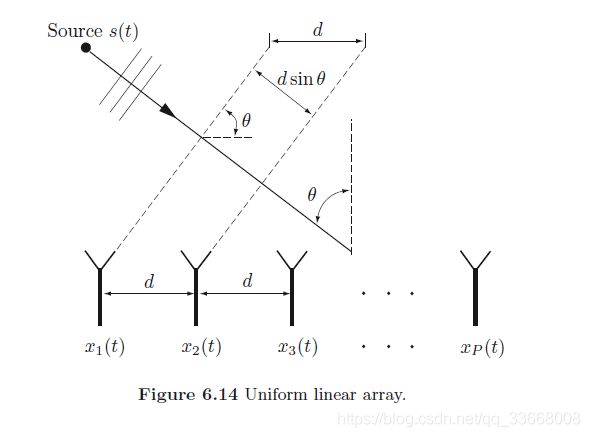
考虑一个简单的ULA模型。

假设DOA（波达方向）是$\theta$。且接收端配置有$P$个线性传感器阵列，则有：
$$\mathbf{y}(t)=\mathbf{a}(\theta )s(t)$$
其中导向矢量$\mathbf{a}(\theta )$为：
$$\mathbf{a}(\theta )={\left[1,e^{-j2\pi d\sin (\theta )/\lambda },\dots ,e^{-j2\pi d(P-1)\sin (\theta )/\lambda }\right]}^T\in {\mathbb{C}}^P$$
$\lambda$为波长。$s(t)$为源信号。

源信号的估计值为：
$$\hat{s}(t)={\mathbf{w}}^H\mathbf{y}(t)={\mathbf{w}}^H\mathbf{a}(\theta )s(t)$$
其中$\mathbf{w}\in {\mathbb{C}}^P$是波束成形权重。令${\theta }_{\mathrm{d}\mathrm{e}\mathrm{s}}\in [-\pi /2,\pi /2]$是期望方向，并假设是完全已知的。一个简单的波束成形可以表示为$\mathbf{w}=\mathbf{a}\left({\theta }_{\mathrm{d}\mathrm{e}\mathrm{s}}\right)$。但它对旁瓣的抑制效果很差。（如下图Yoshiki，$P=20$，$d/\lambda =0.5$，${\theta }_{\mathrm{d}\mathrm{e}\mathrm{s}}=10^{。}$）

接收波束成形：平均旁瓣能量最小化

令：
$$\mathbf{\Omega }=\left[-\pi /2,{\theta }_{\ell }\right]\cup \left[{\theta }_u,\pi /2\right]$$
表示旁瓣带。旁瓣能量最小化问题表示为：
$$\begin{array}{rl}\underset{\mathbf{w}\in {\mathbb{C}}^P}{\min }& {\int }_{\Omega }{\left|{\mathbf{w}}^H\mathbf{a}(\theta )\right|}^{2}d\theta \\ \text{ s.t. }& {\mathbf{w}}^H\mathbf{a}\left({\theta }_{\text{des }}\right)=1\end{array}$$
当$\theta ={\theta }_{\mathrm{d}\mathrm{e}\mathrm{s}}$时，所涉及的波束成形的输出$\hat{s}(t)$就是$s(t)$，而当$\theta \ne {\theta }_{\text{des }}$我们尝试最小化$\mathbf{\Omega }$上的残差总功率，但是源信号估计值与实际值之间仍存在非零残差，该问题等价于一个等式约束的QP问题。
$$\begin{array}{rl}\underset{\mathbf{w}\in {\mathbb{C}}^P}{\min }& \left\{f(\mathbf{w})\triangleq {\mathbf{w}}^H{\mathbf{P}}_{\mathbf{w}}\right\}\\ \text{ s.t. }& {\mathbf{w}}^H\mathbf{a}\left({\theta }_{\text{des }}\right)=1\end{array}$$
其中$$\mathbf{P}={\int }_{\Omega }\mathbf{a}(\theta ){\mathbf{a}}^H(\theta )d\theta ={\mathbf{P}}^H⪰0$$

接收波束成形：最大旁瓣能量最小化

最大旁瓣能量最小化问题表示为
$$\begin{array}{r}{\min }_{\mathbf{w}\in {\mathbb{C}}^P}{\max }_{\theta \in \Omega }{\left|{\mathbf{w}}^H\mathbf{a}(\theta )\right|}^2\\ \text{ s.t. }{\mathbf{w}}^H\mathbf{a}\left({\theta }_{\text{des }}\right)=1\end{array}$$
考虑epigraph，有：
$$\begin{array}{rl}{\min }_{\mathbf{w}\in {\mathbb{C}}^P,t\in \mathbb{R}}& t\\ \text{ s.t. }& {\left|{\mathbf{w}}^H\mathbf{a}(\theta )\right|}^2\le t,\forall \theta \in \Omega \\ & {\mathbf{w}}^H\mathbf{a}\left({\theta }_{\text{des }}\right)=1\end{array}$$
这是无穷多约束下的QCQP，其中的不等式约束可以表示为：
$${\left|{\mathbf{w}}^H\mathbf{a}(\theta )\right|}^2-t={\mathbf{w}}^H\mathbf{P}(\theta )\mathbf{w}-t$$
其中$\mathbf{P}(\theta )=\mathbf{a}(\theta ){\mathbf{a}}^H(\theta )⪰0$。由于约束项是$\mathbf{w}\in {\mathbb{C}}^P$的一个二次凸函数与$t\in \mathbb{R}$的一个线性函数的和，因此在$(\mathbf{w},t)$是凸的，将其表示为标准的QCQP问题
$$\begin{array}{ll}{\min }_{\mathbf{w},t}& \left[\begin{array}{ll}{0}_P^T& 1\end{array}\right]\left[\begin{array}{c}\mathbf{w}\\ t\end{array}\right]\\ \text{ s.t. }& \left[\begin{array}{ll}{\mathbf{w}}^H& t\end{array}\right]\left[\begin{array}{cc}\mathbf{P}(\theta )& 0_P\\ 0_P^T& 0\end{array}\right]\left[\begin{array}{c}\mathbf{w}\\ t\end{array}\right]+\left[\begin{array}{l}{0}_P^T-1\end{array}\right]\left[\begin{array}{c}\mathbf{w}\\ t\end{array}\right]\le 0,\forall \theta \in \Omega \\ & \left[{\mathbf{w}}^{H}t\right]\left[\begin{array}{c}\mathbf{a}\left({\theta }_{\text{des }}\right)\\ 0\end{array}\right]=1\end{array}$$
最大情况的旁瓣能量最小化问题利用离散方式近似。即：${\theta }_1,{\theta }_2,\dots ,{\theta }_L$是$\Omega$中的采样点集合。无穷多约束的QCQP问题表示为：
$$\begin{array}{ll}{\min }_{\mathbf{w},t}& t\\ \text{ s.t. }& {\left|{\mathbf{w}}^H\mathbf{a}\left({\theta }_i\right)\right|}^2\le t,i=1,\dots ,L\\ & {\mathbf{w}}^H\mathbf{a}\left({\theta }_{\text{des }}\right)=1\end{array}$$

下图给出了两种设计的性能图

QCQP在认知无线电(cognitive radio)发射beamforming的应用

问题描述：某次用户想要使用$K$个主用户已经使用的频谱资源。当次用户发现频谱空洞时，使用已授权用户的频谱资源时，必须保证它的通信不会影响到已授权用户的通信，一旦该频道被主用户使用，次用户需要切换到其他空闲频段，或者继续使用该频段，但是改变发射功率活或调制方案避免对主用户的干扰。

符号：

• ${\mathbf{h}}_{SS}\in {\mathbb{C}}^{N_S}$: 次发射机到次接收机的信道向量
• ${\mathbf{h}}_{Sk}\in {\mathbb{C}}^{N_S}$: 次发射机到第$k$个主接收机的信道向量
• ${\mathbf{h}}_{kS}\in {\mathbb{C}}^{N_k}$: 第$k$个主发射机到次接收机的信道向量
• $N_S$：此发射机的天线数目
• $N_k$：第$k$个主发射机的天线数目
• ${\mathbf{w}}_k\in {\mathbb{C}}^{N_k}$：第$k$个主发射机的波束成形向量
• ${\mathbf{w}}_S\in {\mathbb{R}}^{N_S}$：次发射机的波束成形向量S
• ${\sigma }_S^2$：接收机处噪声功率

假定接收均为单天线，发射信号都是单位功率的，则次接收机接收到的SINR可以表示为 ：
$${\gamma }_S=\frac{{\left|{\mathbf{h}}_{SS}^H{\mathbf{w}}_S\right|}^2}{{\sum }_{k=1}^K{\left|{\mathbf{h}}_{kS}^H{\mathbf{w}}_k\right|}^2+{\sigma }_S^2}$$

第$k$个主发射机收到来自次发射的干扰，设其信号功率为${\left|{\mathbf{h}}_{Sk}^H{\mathbf{w}}_S\right|}^2$。设计目标：设计一个次发射波束成形向量${\mathbf{W}}_S$使得${\gamma }_S$最大化，同时，第$k$个主发射机的功率干扰小于阈值${ϵ}_k$。即：
$$\begin{array}{ll}{\max }_{{\mathbf{w}}_S}& {\gamma }_S\\ \text{ s.t. }& {\left|{\mathbf{h}}_{Sk}^H{\mathbf{w}}_S\right|}^2\le {ϵ}_k,k=1,\dots ,K\\ & {\Vert {\mathbf{w}}_S\Vert }_2^2\le P_S\end{array}$$
$P_S$是次链路的最大传输功率。定义：
$$\mathbf{A}={\mathbf{h}}_{SS}{\mathbf{h}}_{SS}^H，{\mathbf{B}}_k={\mathbf{h}}_{Sk}{\mathbf{h}}_{Sk}^H,k=1,\dots ,K$$
其中$\mathbf{A}$和${\mathbf{B}}_k$都是rank-1矩阵。原问题等价以下的QCQP为：
$$\begin{array}{lc}{\min }_{{\mathbf{w}}_S}& -{\mathbf{w}}_S^H\mathbf{A}{\mathbf{w}}_S\\ \text{ s.t. }& {\mathbf{w}}_S^H{\mathbf{B}}_k{\mathbf{w}}_S\le {ϵ}_k,k=1,\dots ,K\\ & {\mathbf{w}}_S^H{\mathbf{w}}_S\le P_S\end{array}$$
由于目标函数是非凸的，所以该问题是非凸的。后续解决办法（SDR）