剑指offer JZ77 按之字形顺序打印二叉树

Java JZ77 按之字形顺序打印二叉树

---

---

   使用双栈法和队列+reverse()法解决剑指offer JZ77 按之字形顺序打印二叉树的问题。

---

一、题目描述

  给定一个二叉树，返回该二叉树的之字形层序遍历，（第一层从左向右，下一层从右向左，一直这样交替）

  数据范围：0≤n≤1500,树上每个节点的val满足 ∣val∣<=1500。
  要求：空间复杂度：O(n)，时间复杂度：O(n)。
  例如：给定的二叉树是{1,2,3,#,#,4,5}

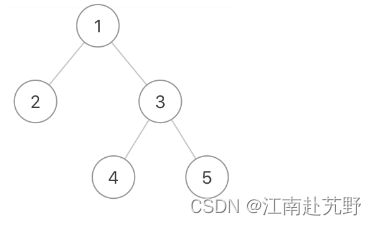
  该二叉树之字形层序遍历的结果是
  [
  [1],
  [3,2],
  [4,5]
  ]

  示例1

输入：{1,2,3,#,#,4,5}
返回值：[[1],[3,2],[4,5]]

  说明：如题面解释，第一层是根节点，从左到右打印结果，第二层从右到左，第三层从左到右。

  示例2

输入：{8,6,10,5,7,9,11}
返回值：[[8],[10,6],[5,7,9,11]]

  示例3

输入：{1,2,3,4,5}
返回值：[[1],[3,2],[4,5]]

二、双栈法

  知识点：栈

  栈是一种仅支持在表尾进行插入和删除操作的线性表，这一端被称为栈顶，另一端被称为栈底。元素入栈指的是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；元素出栈指的是从一个栈删除元素又称作出栈或退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。
  我们可以利用两个栈遍历这棵二叉树，第一个栈L_R从根节点开始记录第一层，然后依次遍历两个栈，遍历第一个栈时遇到的子节点依次加入第二个栈R_L中，即是第二层。
  而遍历第二个栈R_L的时候因为是先进后出，因此就是逆序的，再将第二个栈R_L的子节点依次加入第一个栈L_R中。于是原本的逆序在第一个栈L_R中又变回了正序，如果反复交替直到两个栈都空为止。

public class Solution {
    public ArrayList > Print(TreeNode pRoot) {
//一个二维的ArrayList，其中每个元素都是一个ArrayList类型的对象。
        ArrayList > listAll = new ArrayList<>();
//如果是空，则直接返回空
        if (pRoot == null) {
            return listAll;
        }
        Stack L_R = new Stack();   //第一个栈，存放奇数行，从左打印的行
        Stack R_L = new Stack();	 //第一个栈，存放偶数行，从右打印的行
        int level = 1;		//记录数层
        L_R.push(pRoot);	//放入根节点
 //循环遍历，直到某个奇数行或者偶数行为空
        while (!L_R.isEmpty() || !R_L.isEmpty()) {
            ArrayList list = new ArrayList<>();	//二维矩阵中的行对象，用来短暂保存每层节点数
 //level++ % 2，level先取余后加，判断是否为奇数行
            if (level++ % 2 != 0) {		
                while (!L_R.isEmpty()) {		
                    TreeNode node = L_R.pop();	//先将奇数层的节点保存进list
                    list.add(node.val);
//下一层是偶数层是从右打印，栈先进后出，所以先保存左子节点
                    if (node.left != null) {
                        R_L.push(node.left);
                    }
                    if (node.right != null) {	//再保存右子节点
                        R_L.push(node.right);
                    }
                }
            } else {   //如果是偶数行
                while (!R_L.isEmpty()) {
                    TreeNode node = R_L.pop();	//先将偶数层的节点保存进list
                    list.add(node.val);
                    System.out.println(node.val);
//下一层是奇数层是从左打印，栈先进后出，所以先保存右子节点，再保存左子节点
                    if (node.right != null){
                        L_R.push(node.right);
                    }
                    if (node.left != null){
                        L_R.push(node.left);
                    }
                }
            }
            listAll.add(list);		//每层节点遍历后，将保存该层节点的list整体加入到 二维listAll中
        }
        return listAll;		//遍历结束返回二维listAll
    }

}

三、队列+reverse()法

  知识点：队列

  队列是一种仅支持在表尾进行插入操作、在表头进行删除操作的线性表，插入端称为队尾，删除端称为队首，因整体类似排队的队伍而得名。它满足先进先出的性质，元素入队即将新元素加在队列的尾，元素出队即将队首元素取出，它后一个作为新的队首。
reverse()函数
  在Java中，Collections是一个工具类，提供了一系列静态方法，用于操作集合类。其中，reverse()函数是Collections类中的一个静态方法，用于对List类型的集合进行反转操作。该函数的定义如下：

public static void reverse(List list)

  其中，list表示要进行反转操作的List集合。该函数会将List集合中的元素按照相反的顺序重新排列。需要注意的是，该函数会直接修改原始的List集合，而不是返回一个新的List集合。

  解题思路：

  按照层次遍历按层打印二叉树的方式，每层分开打印，然后对于每一层利用flag标记，第一层为false，之后每到一层取反一次，如果该层的flag为true，则记录的数组整个反转即可。

  但是难点在于如何每层分开存储，从哪里知晓分开的时机？
  在层次遍历的时候，我们通常会借助队列（queue）。当根节点进入队列时，队列长度为1，第一层节点数也为1；若是根节点有两个子节点，push进队列后，队列长度为2，第二层节点数也为2；若是根节点一个子节点，push进队列后，队列长度为为1，第二层节点数也为1。由此，我们可知，每层的节点数等于进入该层时队列长度，因为刚进入该层时，这一层每个节点都会push进队列，而上一层的节点都出去了。

  具体做法：
 ● step 1：首先判断二叉树是否为空，空树没有打印结果。
 ● step 2：建立辅助队列，根节点首先进入队列。不管层次怎么访问，根节点一定是第一个，那它肯定排在队伍的最前面，初始化flag变量。
 ● step 3：每次进入一层，统计队列中元素的个数，更改flag变量的值。因为每当访问完一层，下一层作为这一层的子节点，一定都加入队列，而再下一层还没有加入，因此此时队列中的元素个数就是这一层的元素个数。
 ● step 4：每次遍历这一层这么多的节点数，将其依次从队列中弹出，然后加入这一行的一维数组中，如果它们有子节点，依次加入队列排队等待访问。
step 5：访问完这一层的元素后，根据flag变量决定将这个一维数组直接加入二维数组中还是反转后再加入，然后再访问下一层。（奇数行反转，偶数行不反转）。

import java.util.*;
public class Solution {
    public ArrayList > Print(TreeNode pRoot) {
        TreeNode head = pRoot;
        ArrayList > res = new ArrayList>();
        if(head == null)
            //如果是空，则直接返回空list
            return res;
        //队列存储，进行层次遍历
        Queue temp = new LinkedList();
        temp.offer(head);
        TreeNode p;
        boolean flag = true;
        while(!temp.isEmpty()){
            //记录二叉树的某一行
            ArrayList row = new ArrayList(); 
            int n = temp.size();
            //奇数行反转，偶数行不反转
            flag = !flag;
            //因先进入的是根节点，故每层节点多少，队列大小就是多少
            for(int i = 0; i < n; i++){
                p = temp.poll();
                row.add(p.val);
                //若是左右孩子存在，则存入左右孩子作为下一个层次
                if(p.left != null)
                    temp.offer(p.left);
                if(p.right != null)
                    temp.offer(p.right);
            }
            //奇数行反转，偶数行不反转
            if(flag) 
                Collections.reverse(row);
            res.add(row);
        }
        return res;
    }
}